【Peng-Robinson状态方程】计算纯组分系统的z因子和逸度系数、计算多组分系统的z因子和逸度系数、计算泡点压力、计算露点压力研究（Matlab代码实现）

Ps.729

于 2025-04-30 11:43:05 发布

阅读量506

点赞数 8

文章标签： matlab 数据结构算法

本文链接：https://blog.csdn.net/weixin_67304359/article/details/147627308

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

PR状态方程简介

计算纯组分系统的z因子和逸度系数

计算多组分系统的z因子和逸度系数

计算泡点压力和露点压力

一、Peng-Robinson状态方程基本形式与参数定义

二、纯组分系统的z因子与逸度系数计算

1. z因子计算

2. 逸度系数计算

三、多组分系统的z因子与逸度系数计算

1. 混合规则

2. z因子计算

3. 逸度系数计算

四、泡点压力计算

1. 理论依据

2. 迭代步骤

五、露点压力计算

1. 理论依据

六、Matlab代码实现要点

1. 函数模块

2. 核心算法

七、应用案例与误差分析

1. 案例：CO₂-H₂O系统

2. 高压天然气系统

八、总结与展望

📚2 运行结果

2.1 fugacitycoef

2.2 phasefraction

2.3 pressbub

2.4 tpdss

2.5 vaporliquideq

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

Peng-Robinson状态方程（PR状态方程）在化学工程领域中有着广泛的应用，特别适用于描述含有轻烃、重烃、醇类和其他含氢键分子的复杂流体系统。以下是关于PR状态方程在计算纯组分系统、多组分系统的z因子和逸度系数，以及泡点压力和露点压力方面的详细研究文档：

PR状态方程简介

PR状态方程的形式为：

P=RT/(V−b)−a/(V2+2Vb−b2)

其中，P为压力，T为温度，R为气体常数，V为摩尔体积，a为偏分子体积，b为偏摩尔体积。该方程能够较好地模拟液体和蒸汽之间的相变过程，比经典的范德华斯方程在处理非理想气体行为时更为准确。

计算纯组分系统的z因子和逸度系数

z因子计算：
- z因子是实际气体压缩性与理想气体压缩性的比值，计算公式为Z=PV/(nR*T)。
- 在PR状态方程中，通过给定的P、T以及物质的临界参数（临界温度Tc、临界压力Pc和偏心因子ω），可以求解出摩尔体积V，进而计算出z因子。
逸度系数计算：
- 逸度系数是衡量一个组分在混合物中相对于理想气体行为偏离的程度。
- 在PR状态方程中，逸度系数φ通常通过迭代方法求解，它依赖于系统的压力、温度和组分的临界参数。

计算多组分系统的z因子和逸度系数

z因子计算：
- 对于多组分系统，z因子是各组分z因子的平均值或加权平均值，这取决于系统的具体条件和计算方法。
- 在PR状态方程中，多组分系统的z因子计算通常需要考虑组分间的相互作用，这可以通过引入二元作用系数来实现。
逸度系数计算：
- 对于多组分系统，每个组分的逸度系数都需要单独计算。
- 在PR状态方程中，多组分系统的逸度系数计算通常涉及复杂的迭代过程，需要同时考虑系统的压力、温度、组分的临界参数以及组分间的相互作用。

计算泡点压力和露点压力

泡点压力计算：
- 泡点压力是指在一个恒定温度下，液体开始转变为蒸汽时的压力。
- 在PR状态方程中，泡点压力可以通过逐步降低系统的压力并观察相变的发生来确定。这通常涉及复杂的迭代过程，以找到满足相平衡条件的压力值。
露点压力计算：
- 露点压力是在恒定温度下，蒸汽开始转变为液体时的压力。
- 与泡点压力类似，露点压力也可以通过逐步降低系统的压力并观察相变的发生来确定。在PR状态方程中，这同样需要复杂的迭代过程来找到满足相平衡条件的压力值。

主要功能如下。

(1) 计算纯组分系统的z因子和逸度系数。

fugcoef_purecomp.m：如果找到多个根，则返回使吉布斯自由能最小化的z因子。
fugcoef_purecomp_liquid.m：如果找到多个根，则返回最小z因子。
fugcoef_purecomp_vapor.m：如果找到多个根，则返回最大z因子。

(2)计算多组分系统的z因子和逸度系数。

fugcoef_multicomp.m：如果找到多个根，则返回使吉布斯自由能最小化的z因子。
fugcoef_multicomp_liquid.m：如果找到多个根，则返回最小z因子。
fugcoef_multicomp_vapor.m：如果找到多个根，则返回最大z因子。

(3) 计算泡点压力。

pressbub_purecomp_ss.m：用于纯组分系统。采用连续替代法。
pressbub_purecomp_newton.m：用于纯组分系统。使用牛顿法。
pressbub_multicomp.m：用于多组分系统。采用连续替代法。

(4) 计算露点压力。

pressdew_multicomp.m：用于多组分系统。采用连续置换法。

一、Peng-Robinson状态方程基本形式与参数定义

Peng-Robinson（PR）方程是立方型状态方程，其形式为：

注：Tc为临界温度，Pc为临界压力，ω为偏心因子，Tr=T/Tc为对比温度。

二、纯组分系统的z因子与逸度系数计算

1. z因子计算

z因子定义为实际气体摩尔体积与理想气体摩尔体积的比值：

根的选择原则：

气相：选择最大实根（对应低密度状态）。
液相：选择最小实根（对应高密度状态）。
多根情况：通过比较吉布斯自由能（最小化原则）确定稳定相态。

2. 逸度系数计算

逸度系数ϕ由积分公式导出：

结合PR方程，推导出具体表达式：

注：此公式通过状态方程参数A、B和Z直接计算逸度系数。

三、多组分系统的z因子与逸度系数计算

1. 混合规则

多组分系统的aa和bb参数通过混合规则计算：

van der Waals混合规则：

其中kij为二元相互作用参数，需通过实验拟合。

2. z因子计算

多组分系统的压缩因子方程与纯组分形式相同，但参数AA和BB需替换为混合值：

根的选择原则与纯组分相同，优先选择吉布斯自由能最小的解。

3. 逸度系数计算

组分ii的逸度系数ϕi由下式计算：

注：需结合混合参数和压缩因子迭代求解。

四、泡点压力计算

1. 理论依据

泡点压力是液相开始汽化的压力，需满足：

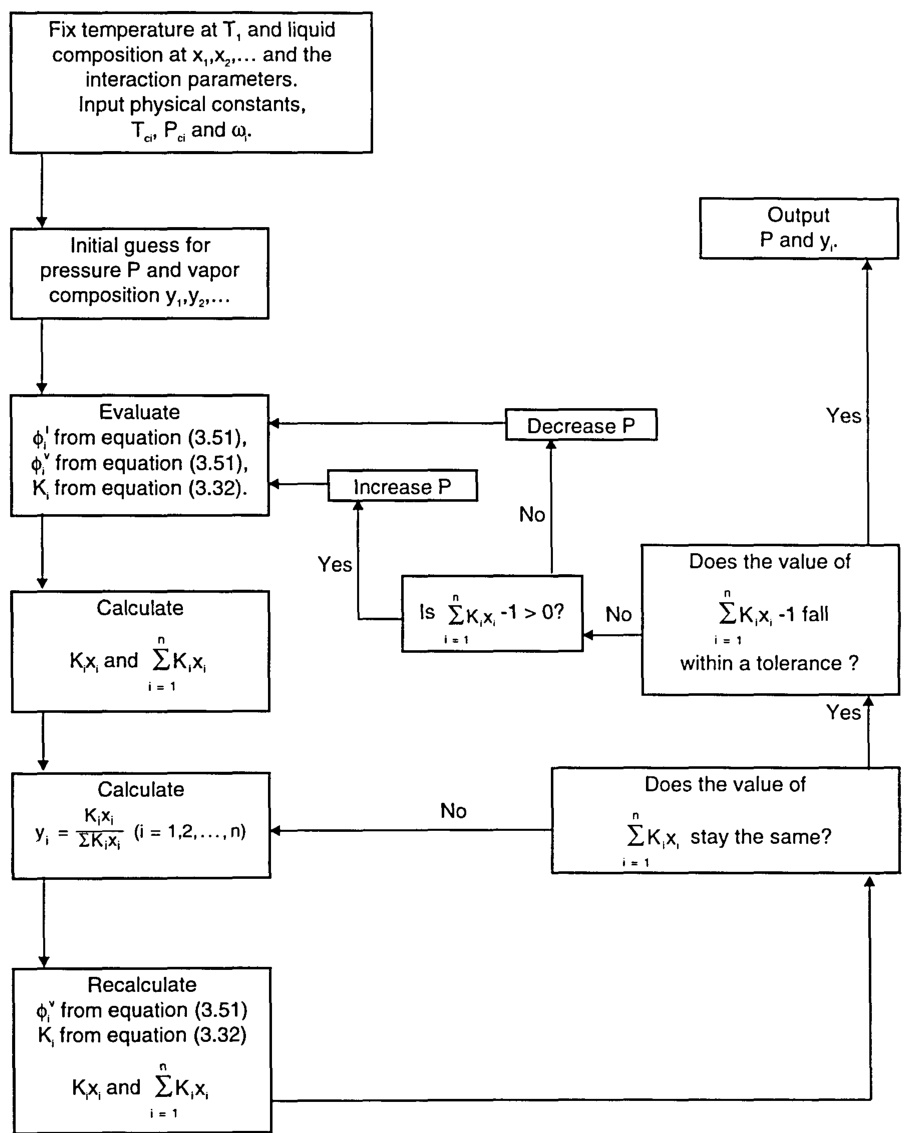
2. 迭代步骤

五、露点压力计算

1. 理论依据

露点压力是气相开始冷凝的压力，需满足：

六、Matlab代码实现要点

1. 函数模块

纯组分系统：
- fugcoef_purecomp.m：自动选择吉布斯自由能最小的ZZ。
- fugcoef_purecomp_liquid.m：强制返回最小ZZ（液相）。
- fugcoef_purecomp_vapor.m：强制返回最大ZZ（气相）。
多组分系统：
- fugcoef_multicomp.m：基于混合规则计算逸度系数。
- pressbub_multicomp.m：泡点压力迭代计算。
- pressdew_multicomp.m：露点压力迭代计算。

2. 核心算法

function [fugcoef, zfactor] = fugacitycoef_multicomp(comp, press, temp, pressc, tempc, acentric, BIP)
    [A, B] = calcab_multicomp(press, temp, pressc, tempc, acentric);
    [Amix, Bmix, Amix2] = calcabmix(comp, A, B, BIP);
    zfactor = calczfactor(Amix, Bmix);
    if size(zfactor,1) > 1
        zfactor = choosezfactor(zfactor, comp, A, B, Amix, Bmix, Amix2);
    end
    fugcoef = calcfugcoef_multicomp(zfactor, A, B, Amix, Bmix, Amix2);
end

注：通过choosezfactor函数选择最优ZZ，确保计算稳定性。

七、应用案例与误差分析

1. 案例：CO₂-H₂O系统

使用PR方程结合Wong-Sandler混合规则，在273–623 K和0.1–200 MPa下，CO₂和H₂O的互溶度计算误差小于7.5%。

2. 高压天然气系统

PR方程在压力高于4 MPa时，露点压力预测误差达4.36%，建议改用GERG2008方程以提高精度。

八、总结与展望

PR方程因其简洁性和通用性，广泛应用于工程相平衡计算，但在高压、强极性体系中需结合混合规则改进。未来研究可探索：

引入量子化学参数优化二元相互作用参数kijkij。
结合机器学习方法加速迭代收敛。

📚2 运行结果

2.1 fugacitycoef

2.2 phasefraction

2.3 pressbub

2.4 tpdss

2.5 vaporliquideq

部分代码“

%% CALCULATE THE FUGACITY COEFFICIENT AND Z-FACTOR OF MULTI-COMPONENT SYSTEMS
% -------------------------------------------------------------------------
% The Definition of Variables.
% comp : composition
% press : pressure
% temp : temperature
% pressc : critical pressure
% tempc : critical temperature
% acentric: acentric factor
% BIP : binary interaction parameter
% fugcoef : fugacity coefficient
% zfactor : compressibility factor
% -------------------------------------------------------------------------
% In this function, an appropriate z-factor is automatically chosen
% according to gibbs free energy if multiple roots are found.
function [fugcoef, zfactor] = fugacitycoef_multicomp(comp, press, temp, pressc, tempc, acentric, BIP)

[A, B] = calcab_multicomp(press, temp, pressc, tempc, acentric);

[Amix, Bmix, Amix2] = calcabmix(comp, A, B, BIP);

zfactor = calczfactor(Amix, Bmix);

if (size(zfactor,1) > 1)
zfactor = choosezfactor(zfactor, comp, A, B, Amix, Bmix, Amix2);
end

fugcoef = calcfugcoef_multicomp(zfactor, A, B, Amix, Bmix, Amix2);

end

%% SEARTCH AND RETURN AN APPROPRIATE Z-FACTOR
% Calculate dimensionless excess gibbs free energy, and return the z
% factor which minimizes the gibbs free energy.
function minzfactor = choosezfactor(zfactor, comp, A, B, Amix, Bmix, Amix2)

gibbsenergy = [];