力扣题解7.27

最新推荐文章于 2024-07-25 08:29:38 发布

原创最新推荐文章于 2024-07-25 08:29:38 发布 · 504 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c语言

这篇博客探讨了如何使用动态规划解决两种网格路径问题：一种是从左上角到右下角的不同路径计数，另一种是寻找网格中数字总和最小的路径。在每种情况下，博主都介绍了动态规划的状态转移方程，并强调了边界条件的重要性。

62. 不同路径

难度中等1481

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

这是一道典型的动态规划，对于第i行第j列的格子到达他的路径只有左侧格子和上方的格子，将每个格子的路径数看做一个二维数组，即

a[i][j]=a[i-1[j]+a[i][j-1]

且需要注意的是当位于边界时的选择至于一种，所以通过循环将a[0][j],a[i][0]设为1

从第1行第1列开始动态规划，输出a[m-1][n-1]即为总路径数。

int uniquePaths(int m, int n) {
    int a[m][n];
    for (int i = 0; i < m; i++) {
        a[i][0] = 1;
    }
    for (int j = 0; j < n; j++) {
        a[0][j] = 1;
    }
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            a[i][j] = a[i - 1][j] + a[i][j - 1];
        }
    }
    return a[m - 1][n - 1];
}

难度中等1301

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

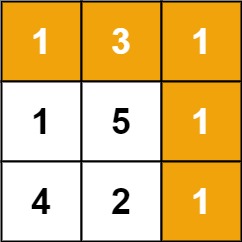
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

这一题与上面的不同路径是十分类似的，同样是使用动态规划来解题。

这里我们需要先设置一个dp数组来存储每个格子的最小和

同样的对于边界上的仅有一种选择，所以

dp[i][0] = dp[i - 1][0] + grid[i][0];

dp[0][j] = dp[0][j - 1] + grid[0][j];

那么对于一般情况便使用dp方程，自身的值加上上一步两格子的最小值便是该格子和的最小值

dp[i][j] = fmin(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];

int minPathSum(int** grid, int gridSize, int* gridColSize) {
    int rows = gridSize, columns = gridColSize[0];
    if (rows == 0 || columns == 0) {
        return 0;
    }
    int dp[rows][columns];
    dp[0][0] = grid[0][0];
    for (int i = 1; i < rows; i++) {
        dp[i][0] = dp[i - 1][0] + grid[i][0];
    }
    for (int j = 1; j < columns; j++) {
        dp[0][j] = dp[0][j - 1] + grid[0][j];
    }
    for (int i = 1; i < rows; i++) {
        for (int j = 1; j < columns; j++) {
            dp[i][j] = fmin(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
        }
    }
    return dp[rows - 1][columns - 1];
}