45天打卡计划_Day10

卖女孩的小火柴_

已于 2025-02-16 20:52:45 修改

阅读量603

点赞数 6

文章标签：算法数据结构

于 2025-02-16 20:52:32 首次发布

本文链接：https://blog.csdn.net/weixin_72162790/article/details/145669753

版权

题目信息 :二叉树的锯齿形层序遍历

知识点：树、二叉树、广度优先搜索

题目描述:

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

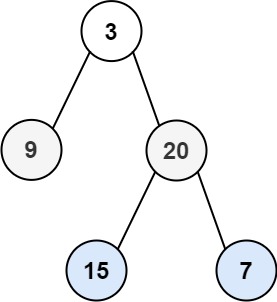
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

数据范围：

树中节点数目在范围 [0, 2000] 内
$-100 \leq Node.val \leq 100$

解题思路：

层序遍历维护一个翻转标识记录每层的遍历顺序，隔层反序即可

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i >0;i--){
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            if(res.size() %2 ==1) Collections.reverse(tmp);
            res.add(tmp);
        }
        return res;
    }
}

复杂度分析：

时间复杂度 $O(N)$ ： N 为二叉树的节点数量，即 BFS 需循环 N 次，占用 $O(N)$ 。共完成少于 N 个节点的倒序操作，占用 $O(N)$ 。
空间复杂度 $O(N)$ ：最差情况下，即当树为满二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 $O(N)$ 大小的额外空间。

题目信息：存在重复元素

知识点：数组、排序、哈希表

题目描述:

给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。

示例 1：

输入：nums = [1,2,3,1]

输出：true

解释：

元素 1 在下标 0 和 3 出现。

示例 2：

输入：nums = [1,2,3,4]

输出：false

解释：

所有元素都不同。

示例 3：

输入：nums = [1,1,1,3,3,4,3,2,4,2]

输出：true

数据范围：

$-10^{9} \leq nums[i] \leq 10^{9}$

解题思路：

对于数组中每个元素，我们将它插入到哈希表中。如果插入一个元素时发现该元素已经存在于哈希表中，则说明存在重复的元素。

写法一

把 nums 中的元素都丢到哈希集合中（去重）。如果哈希集合的大小小于 n，则说明有重复元素。

class Solution {
    public boolean containsDuplicate(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int x : nums) {
            set.add(x);
        }
        return set.size() < nums.length;
    }
}

复杂度分析

时间复杂度： $O(N)$ ，其中 n 是 nums 的长度。
空间复杂度： $O(N)$ 。

写法二:优化方法一剪枝

遍历数组，一边遍历一边把 nums[i] 加到哈希集合中。如果发现 nums[i] 已经在哈希集合中，直接返回 true。这样可以提前退出循环。

class Solution {
    public boolean containsDuplicate(int[] nums) {
    Set<Integer> set = new HashSet<>();
    for(int x : nums) {
        if(!set.add(x)) {
            return true;
        }
    }
    return false;
    }
}