2月7日刷题总结

P1802 5 倍经验日

题目背景

现在乐斗有活动了！每打一个人可以获得 5 倍经验！absi2011 却无奈的看着那一些比他等级高的好友，想着能否把他们干掉。干掉能拿不少经验的。

题目描述

现在 absi2011 拿出了 xx 个迷你装药物（嗑药打人可耻…），准备开始与那些人打了。

由于迷你装药物每个只能用一次，所以 absi2011 要谨慎的使用这些药。悲剧的是，用药量没达到最少打败该人所需的属性药药量，则打这个人必输。例如他用 22 个药去打别人，别人却表明 33 个药才能打过，那么相当于你输了并且这两个属性药浪费了。

现在有 nn 个好友，给定失败时可获得的经验、胜利时可获得的经验，打败他至少需要的药量。

要求求出最大经验 ss，输出 5s5s。

输入格式

第一行两个数，nn 和 xx。

后面 nn 行每行三个数，分别表示失败时获得的经验 \mathit{lose}_ilosei，胜利时获得的经验 \mathit{win}_iwini 和打过要至少使用的药数量 \mathit{use}_iusei。

输出格式

一个整数，最多获得的经验的五倍。

输入输出样例

输入 #1复制

6 8

21 52 1

21 70 5

21 48 2

14 38 3

14 36 1

14 36 2

输出 #1复制

1060

说明/提示

【Hint】

五倍经验活动的时候，absi2011 总是吃体力药水而不是这种属性药。

【数据范围】

• 对于 10\%10% 的数据，保证 x=0x=0。

• 对于 30\%30% 的数据，保证 0\le n\le 100≤n≤10，0\le x\le 200≤x≤20。

• 对于 60\%60% 的数据，保证 0\le n,x\le 1000≤n,x≤100， 10<lose_i,win_i\le 10010<losei,wini≤100，0\le use_i\le 50≤usei≤5。

• 对于 100\%100% 的数据，保证 0\le n,x\le 10^30≤n,x≤103，0<lose_i\le win_i\le 10^60<losei≤wini≤106，0\le use_i\le 10^30≤usei≤103。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

思路：转化为0/1背包进行求解，将输了之后的作为基础值，差值变成价值

0/1背包dp过程详解：

6 8

w a

52 1

70 5

48 2

38 3

36 1

36 2

dp数组状态：0 0 0 0 0 0 0 0

i=1;

dp[8]=max(dp[8],dp[8-1]+a[1]);

dp[7]=max(dp[7],dp[7-1]+a[1]);

dp[6]=max(dp[6],dp[6-1]+a[1]);

dp[5]=max(dp[5],dp[5-1]+a[1]);

dp[4]=max(dp[4],dp[4-1]+a[1]);

dp[3]=max(dp[3],dp[3-1]+a[1]);

dp[2]=max(dp[2],dp[2-1]+a[1]);

dp[1]=max(dp[1],dp[1-1]+a[1]);

dp数组状态：52 52 52 52 52 52 52 52

i=2;

dp[8]=max(dp[8],dp[8-5]+a[2]);

dp[7]=max(dp[7],dp[7-5]+a[2]);

dp[6]=max(dp[6],dp[6-5]+a[2]);

dp[5]=max(dp[5],dp[5-5]+a[2]);

dp数组状态：52 52 52 52 122 122 122 122

i=3

dp[8]=max(dp[8],dp[8-3]+a[3]);

dp[7]=max(dp[7],dp[7-3]+a[3]);

dp[6]=max(dp[6],dp[6-3]+a[3]);

dp[5]=max(dp[5],dp[5-3]+a[3]);

dp[4]=max(dp[4],dp[4-3]+a[3]);

dp[3]=max(dp[3],dp[3-3]+a[3]);

dp数组状态：52 52 100 100 100 100 100 170

i=4;

dp[8]=max(dp[8],dp[8-3]+a[4]);

dp[7]=max(dp[7],dp[7-3]+a[4]);

dp[6]=max(dp[6],dp[6-3]+a[4]);

dp[5]=max(dp[5],dp[5-3]+a[4]);

dp[4]=max(dp[4],dp[4-3]+a[4]);

dp[3]=max(dp[3],dp[3-3]+a[4]);

dp数组状态 52 52 138 138 138 138 138 170

i=5;

dp[8]=max(dp[8],dp[8-1]+a[5]);

dp[7]=max(dp[7],dp[7-1]+a[5]);

dp[6]=max(dp[6],dp[6-1]+a[5]);

dp[5]=max(dp[5],dp[5-1]+a[5]);

dp[4]=max(dp[4],dp[4-1]+a[5]);

dp[3]=max(dp[3],dp[3-1]+a[5]);

dp[2]=max(dp[2],dp[2-1]+a[5]);

dp[1]=max(dp[1],dp[1-1]+a[5]);

dp数组状态：88 88 174 174 174 174 174 174

i=6;

dp[8]=max(dp[8],dp[8-2]+a[6]);

dp[7]=max(dp[7],dp[7-2]+a[6]);

dp[6]=max(dp[6],dp[6-2]+a[6]);

dp[5]=max(dp[5],dp[5-2]+a[6]);

dp[4]=max(dp[4],dp[4-2]+a[6]);

dp[3]=max(dp[3],dp[3-2]+a[6]);

dp[2]=max(dp[2],dp[2-2]+a[6]);

dp数组状态 88 134 174 174 174 174 174 174

以上为dp过程详解，但不是用差值作为价值dp。差值原理是一致的。只是数值可能不一样。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
int max_(int x,int y)
{
    return x>y?x:y;
}
long long dp[1005];//开long long
int main()
{
    int n,x,lose[1005]={0},win[1005]={0},a[1005]={0},f[1005],tmp=0;
    scanf("%d%d",&n,&x);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&lose[i],&win[i],&a[i]);
        tmp+=lose[i];//基础值累加存起来
        f[i]=win[i]-lose[i];//用差值作为dp的价值
    }
    for(int i=1;i<=n;i++)//各个好友依次遍历
    {
        for(int j=x;j>=a[i];j--)
        {
            dp[j]=max_(dp[j],dp[j-a[i]]+f[i]); //dp过程详情见上文
        }
    }
    long long ans=(dp[x]+tmp)*5;
    printf("%lld",ans);
}

P1002 [NOIP2002 普及组] 过河卒

# [NOIP2002 普及组] 过河卒

## 题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。


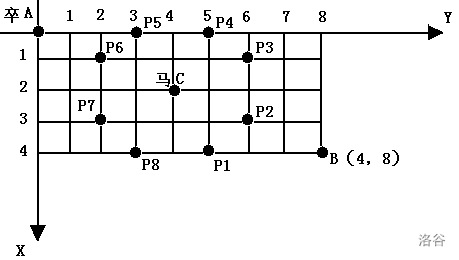
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

## 输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

## 输出格式

一个整数，表示所有的路径条数。

## 样例 #1

### 样例输入 #1

```

6 6 3 3

```

### 样例输出 #1

```

6

```

## 提示

对于 $100 \%$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

**【题目来源】**

NOIP 2002 普及组第四题

思路：首先我们要了解一个公式：

在平面内，从点 (0,0)(0,0) 到点 (x,y)(x,y) 的路径数；

f[x][y]=f[x-1][y]+f[x][y-1]f[x][y]=f[x−1][y]+f[x][y−1]

证明：

该题中，卒只能往下和右走，所以b点只有左边的点和上面的点可以到达

所以：f[x][y]=f[x-1][y]+f[x][y-1]；

再一个我们需要判断左边界和上边界：

上边界:

上边界的时候只有同一行的可以到达，

所以有：f[x][y]=f[x-1][y]；

左边界：

只存在上方的可以到达该点

所以：f[x][y]=f[x][y-1];

还有特殊的起点：f[0][0]没有其他的点可以到这里，所以就只有一条路径

这里解释一下：上述这句话是有点问题的，我们可以这样理解，现有

0 1 2

0 a b c

这么一个坐标系，a作为（0 ，0），若我们要求b的路径数，根据f[x][y]=f[x-1][y]可知，b的路径数等于a的路径数，也就是1条。其实简单一点理解也就是自己到自己也是路径也就是1（也就是上面那句话（虽然有点不好理解））。

代码实现：

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
int n,m,x,y;
long long a[25][25],dp[25][25];
int main()
{    
    scanf("%d%d%d%d",&n,&m,&x,&y);
    a[x][y]=1;
    int next[8][2]={{-1,-2},{1,2},{-1,2},{1,-2},{2,-1},{-2,1},{2,1},{-2,-1}};//马的八步
    for(int i=0;i<8;i++)//马限制点的设置
    {
        int t1=x+next[i][0];
        int t2=y+next[i][1];
        if(t1>=0&&t2<=20)//判断越界
        {
            a[t1][t2]=1;
        }
    }
    //dp过程
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            if(a[i][j]!=1)//该点没有被马限制
            {
                if((i==0&&j==0))//0,0点特殊处理
                {
                    dp[i][j]=1;
                }
                else if(i==0&&j>0)//上边界
                {
                    dp[i][j]=dp[i][j-1];
                }
                else if(i>0&&j==0)//左边界
                {
                    dp[i][j]=dp[i-1][j];
                }
                else dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }
    }
    printf("%lld",dp[n][m]);
}