[机器学习]主成分分析(PCA)

Fxrain

已于 2024-06-19 13:35:10 修改

阅读量796

点赞数 14

文章标签：机器学习人工智能

于 2024-06-14 19:04:16 首次发布

本文链接：https://blog.csdn.net/weixin_73049545/article/details/139607001

版权

一、算法概述

1.1算法简介

主成分分析（PCA）作为一种常用的数据降维技术，其主要目的是通过线性变换，将原始数据投影到一个新的坐标系中，使得数据在新坐标系中的方差尽可能大，从而减少数据的维度。即找到数据中方差最大的方向，将数据映射到这个方向上，形成第一个主成分。然后，在与第一个主成分正交的方向上找到第二大方差的方向，形成第二个主成分，依此类推。通过选择最大方差的前几个主成分，就可以实现对数据维度的降低。进行降维时，我们希望损失尽可能小，即我们希望降维的标准为：样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。

1.2算法涉及的相关知识

（1）向量的内积

A·B=|A||B|cos(a)，即A向量在B向量的方向上的投影的长度

（2）散度

我们需要找到的超平面需满足最大可分性：样本点在这个超平面上的投影能尽可能分开，这个分开的程度我们称之为散度，散度可以采用方差或协方差来衡量（在机器学中，样本的方差较大时，对最终的结果影响会优于方差较小的样本）

（3）方差/协方差

方差用来形容单个维度的样本的波动程度，协方差指多个维度的样本数据的相关性，协方差公式为 $eq?Cov%28X%2CY%29%3D%5Cfrac%7B%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%28X_%7Bi%7D-%5Cbar%7BX%7D%29%28Y_i-%5Cbar%7BY%7D%29%7D%7B%28n-1%29%7D$

其中Cov(X,Y)∈R，绝对值越大说明相关性越高。PCA的首要目标是让投影后的散度最大，因此我们要对所有的超平面的投影都做一次散度的计算，并找到最大散度的超平面。

1.3算法流程

输入：

样本集 $eq?D%3D%5Cleft%20%5C%7B%20x_1%2Cx_2%2C...%2Cx_m%20%5Cright%20%5C%7D$ ；低维空间维数 $eq?d%5E%7B%27%7D$ .

过程：

1.对所有样本进行中心化（将坐标原点放在数据中心）： $eq?x_i%5Cleftarrow%20x_i-%5Cfrac%7B1%7D%7Bm%7D%5Csum_%7Bi%3D1%7D%5E%7Bm%7Dx_%7Bi%7D$ ；

2.计算样本的协方差矩阵 $eq?XX%5E%7BT%7D$ ；

3.对协方差矩阵 $eq?XX%5E%7BT%7D$ 做特征值分解，得到 $eq?m$ 个特征值并排序：

$eq?%5Clambda%20_1%5Cgeqslant%20%5Clambda%20_2%5Cgeqslant%20%5Ccdots%20%5Cgeqslant%20%5Clambda%20_i%5Cgeqslant%20%5Ccdots%20%5Cgeqslant%20%5Clambda%20_m$ ；

  其中，求前 $eq?d$ 个特征值对应的单位特征向量，第 $eq?i$ 个特征值对应的单位特征向量：

     $eq?%5Cboldsymbol%7B%5Comega%20%7D_i%3D%5Cleft%28%20a_%7B1i%7D%2Ca_%7B2i%7D%2C%5Ccdots%20%2Ca_%7Bmi%7D%20%5Cright%29%20%5ET%2Ci%3D1%2C2%2C%5Ccdots%20%2Cd$ ；

4.取最大的 $eq?d%5E%7B%27%7D$ 个特征值所对应的特征向量 $eq?w_1%2Cw_2%2C...%2Cw_%7Bd%27%7D$ ，构造矩阵    $eq?%5Cboldsymbol%7BW%7D%3D%5Cleft%28%20%5Cboldsymbol%7B%5Comega%20%7D_1%2C%5Cboldsymbol%7B%5Comega%20%7D_2%2C%5Ccdots%20%5Cboldsymbol%7B%5Comega%20%7D_d%20%5Cright%29$ ， $eq?%5Cboldsymbol%7BW%7D$ 是一个 $eq?n%5Ctimes%20d$ 的正交矩阵。其中，第 $eq?i$ 个样本主成分：

   $eq?y_i%3D%7B%5Cboldsymbol%7Ba%7D_i%7D%5ET%5Cboldsymbol%7Bx%7D%2C%20i%3D1%2C2%2C%5Ccdots%20%2Cd$ ；

5. 通过以下映射将 $eq?n$ 维样本映射到 $eq?d$ 维，得到 $eq?d%5Ctimes%20m$ 样本主成分矩阵 $eq?%5Cboldsymbol%7BY%7D$ ： $eq?%5Cboldsymbol%7BY%7D%3D%5Cboldsymbol%7BW%7D%5ET%5Cboldsymbol%7BX%7D$

输出：

投影矩阵 $eq?W%3D%5Cleft%20%28%20w_1%2Cw_2%2C...%2Cw_%7Bd%27%7D%5Cright%20%29$

二、算法原理

2.1 PCA最大方差理论

对于给定的一组数据点 $eq?%5Cleft%20%5C%7B%20v_1%2Cv_2%2C...%2Cv_n%20%5Cright%20%5C%7D$ ，其中所有向量均为列向量，中心化后的表示为

$eq?%5Cleft%20%5C%7B%20x_1%2Cx_2%2C...%2Cx_n%20%5Cright%20%5C%7D%3D%5Cleft%20%5C%7B%20v_1-%7B%5Cmu%20%7D%2Cv_2-%7B%5Cmu%20%7D%2C...%2Cv_n-%7B%5Cmu%20%7D%20%5Cright%20%5C%7D$

其中 $eq?%5Cmu%20%3D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dv_i$ 。向量内积在几何上表示为第一个向量投影到第二个向量上的长度，因此向量 $eq?x_i$ 在ω（单位方向向量）上的投影坐标表示为 $eq?%5Cleft%20%28%20x_i%2C%5Comega%20%5Cright%20%29%3Dx_%7Bi%7D%5E%7BT%7D%5Comega$ 。所以目标是找到一个投影方向ω，使得 $eq?%5Cleft%20%5C%7B%20x_1%2Cx_2%2C...%2Cx_n%20%5Cright%20%5C%7D$ 在ω上的投影方差尽可能大。又投影后均值为0，所以投影后的方差可以表示为：

$eq?D%28x%29%3D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Cleft%20%28%20x_i%5ET%5Comega%20%5Cright%20%29%5E2%3D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Cleft%20%28x_i%5ET%5Comega%20%5Cright%20%29%5ET%5Cleft%20%28x_i%5ET%5Comega%20%5Cright%20%29%3D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Comega%20%5ETx_ix_i%5ET%5Comega%20%3Dw%5ET%5Cleft%20%28%20%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dx_ix_i%5ET%20%5Cright%20%29%5Comega$

其中， $eq?%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Comega%20%5ETx_ix_i%5ET%5Comega$ 为样本的协方差矩阵，将其写作Σ。另外，ω为单位向量，所以 $eq?%5Comega%5ET%20%5Comega%20%3D1$ 。因此问题转换为需要求解一个最大化问题，即 $eq?%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20max%5Cleft%20%5C%7B%20%5Comega%20%5ET%5CSigma%20%5Comega%20%5Cright%20%5C%7D%5C%5C%20s.t.%5Comega%20%5ET%5Comega%3D1%20%5Cend%7Bmatrix%7D%5Cright.$ 。引入拉格朗日乘子，对ω求导令其等于0： $eq?%5Comega%20%5ET%5Csum%20%5Comega%20-%5Clambda%20%28%5Comega%20%5ET%5Comega%20-1%29$ $eq?%5Csum%20%5Comega%20-%5Clambda%20%5Comega%20%3D0$ ，可以推出 $eq?%5Csum%20%5Comega%20%3D%5Clambda%20%5Comega$ ，此时 $eq?D%28x%29%3D%5Comega%20%5ET%5Csum%20%5Comega%20%3D%5Clambda%20%5Comega%20%5ET%5Comega%20%3D%5Clambda$ 。x投影后的方差就是协方差矩阵的特征值。我们要找到最大的方差也就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值所对应的特征向量。次佳投影方向位于最佳投影方向的正交空间中，是第二大特征值对应的特征向量，以此类推。

2.2PCA最小平均方差理论

与PCA最大方差理论得到的结果相同。

三、算法实现

3.1 导入数据

准备数据：导入Scikit-learn库中的鸢尾花数据集

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 鸢尾花的数据集
iris = datasets.load_iris()
print(iris)

输出鸢尾花的数据集结果图如下：

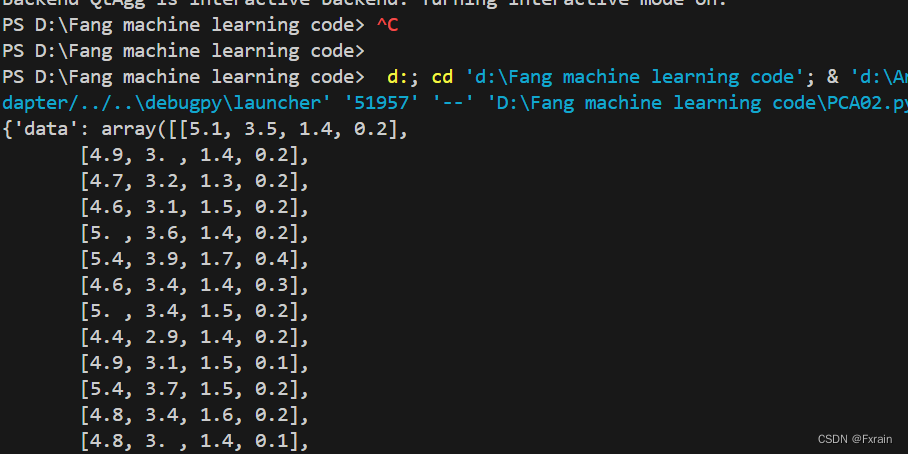
3.2 用PCA进行降维

fit_transform方法：这是PCA类中的方法，可以对原始数据进行降维处理。它首先使用fit方法计算出数据的主成分（特征向量），然后对原始数据进行线性变换，得到降维后的数据。这个方法可以合并fit和transform两个步骤，方便使用。

explained_variance_ratio_属性：这是PCA类中的属性，表示每个主成分保留的方差比例。它返回一个数组，数组的每个元素表示对应主成分保留的方差百分比。通过查看这个属性，我们可以了解每个主成分在总方差中的贡献程度。

explained_variance_ratio_.sum()方法：在PCA中，explained_variance_ratio_.sum()方法可以用来查看当前保留的总方差百分比。总方差百分比越高，说明保留的主成分越多，降维后的数据保留了较多的信息。

components_属性：这是PCA类中的属性，表示主成分（特征值）对应的特征向量。特征向量描述了数据的方向，在PCA中，它可以用来了解数据降维过程中的线性变换规则。同时，通过这个属性，也可以了解每个原始特征在新特征构建过程中的权重。

X=iris['data']
y=iris['target']
print('Before pca: \n', X[:3,:])# 前三行，所有列
 
pca_1 = PCA(n_components=2) # 指定主成分数量初始化  将数据降为2维
X_red_1 = pca_1.fit_transform(X) # fit并直接得到降维结果 
 
# 这里只展示前三行的结果以示对比
print('After pca: \n', X_red_1[:3, :],'\n')

# 查看各个特征值所占的百分比，也就是每个主成分保留的方差百分比
print('方差百分比: ', pca_1.explained_variance_ratio_)    
 
# 当前保留总方差百分比；
 
print('总方差百分比: ',pca_1.explained_variance_ratio_.sum(),'\n')
 
# 线性变换规则
print('components_: \n', pca_1.components_)

因为主成分数量为2，PCA处理过后，数据从四维变成二维，实现降维。结果如下所示：

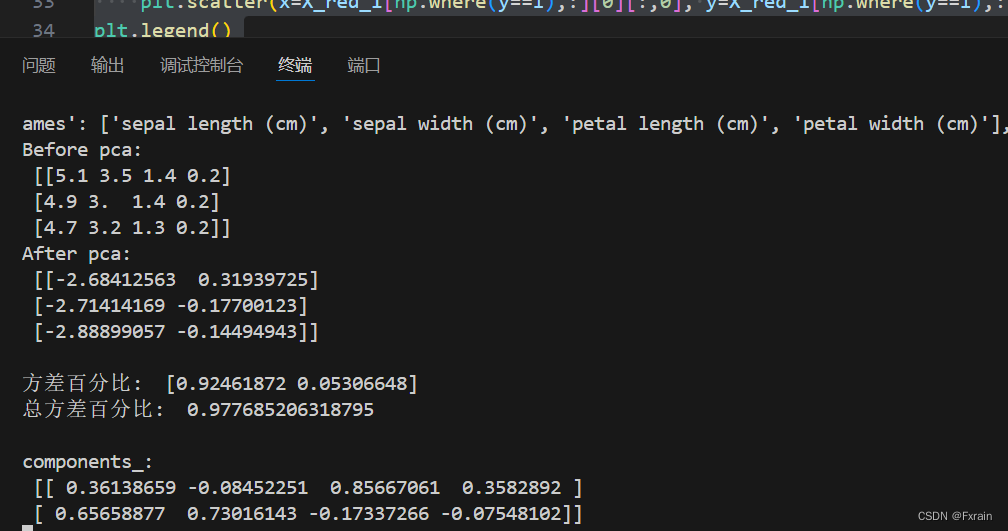
3.3 结果可视化

#结果可视化
plt.figure(figsize=(6,6))    
for i in range(2):
    plt.scatter(x=X_red_1[np.where(y==i),:][0][:,0], y=X_red_1[np.where(y==i),:][0][:,1], alpha=0.8, label='效果%s' % i)
plt.legend()
plt.show()

运行结果图：

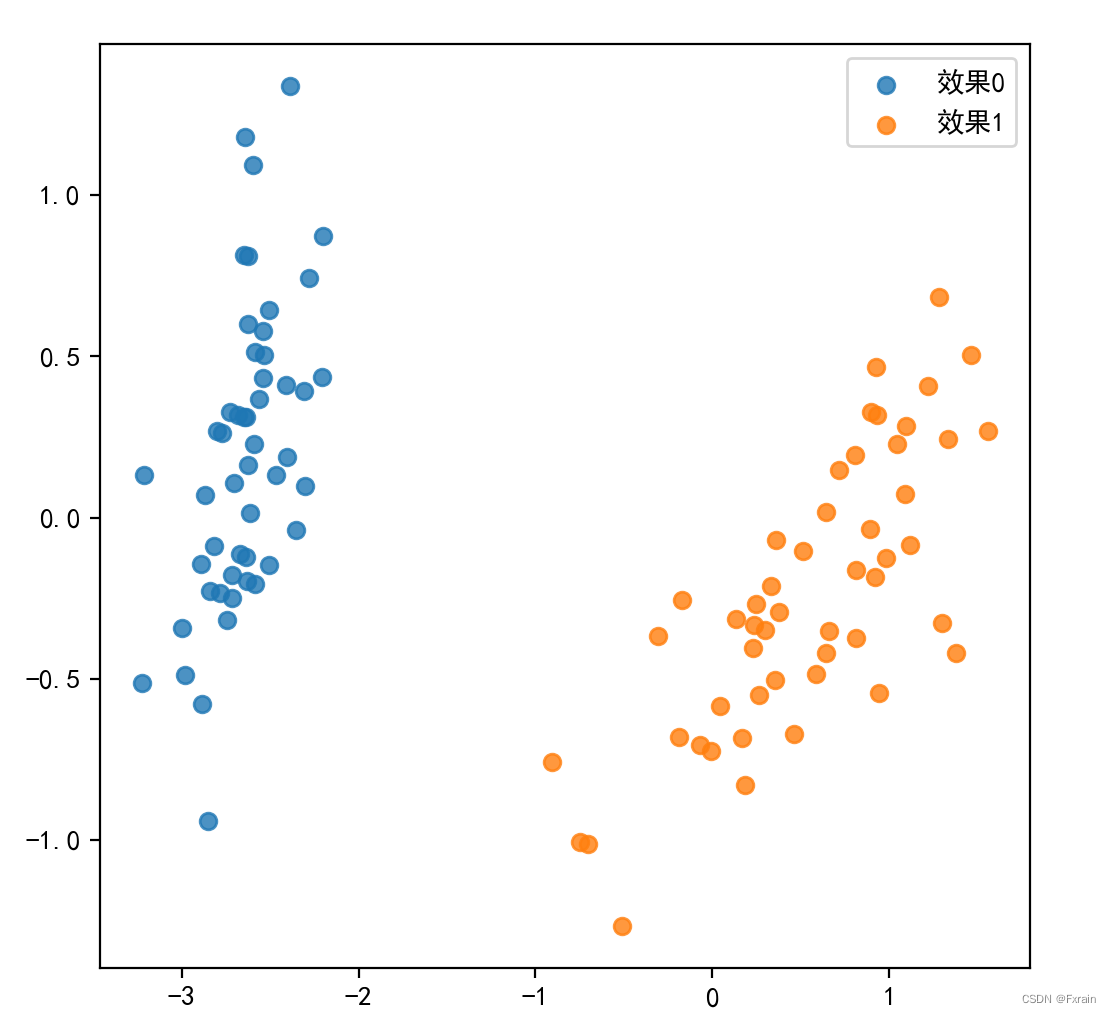
3.4 完整代码展示

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 鸢尾花的数据集
iris = datasets.load_iris()
print(iris)

X=iris['data']
y=iris['target']
print('Before pca: \n', X[:3,:])# 前三行，所有列
 
pca_1 = PCA(n_components=2) # 指定主成分数量初始化  将数据降为2维
X_red_1 = pca_1.fit_transform(X) # fit并直接得到降维结果 
 
# 这里只展示前三行的结果以示对比
print('After pca: \n', X_red_1[:3, :],'\n')

# 查看各个特征值所占的百分比，也就是每个主成分保留的方差百分比
print('方差百分比: ', pca_1.explained_variance_ratio_)    
 
# 当前保留总方差百分比；
 
print('总方差百分比: ',pca_1.explained_variance_ratio_.sum(),'\n')
 
# 线性变换规则
print('components_: \n', pca_1.components_)
#结果可视化
plt.figure(figsize=(6,6))    
for i in range(2):
    plt.scatter(x=X_red_1[np.where(y==i),:][0][:,0], y=X_red_1[np.where(y==i),:][0][:,1], alpha=0.8, label='效果%s' % i)
plt.legend()
plt.show()

四、总结分析

4.1实验小结

本次实验通过PCA实现特征提取（降维）。PCA算法可以简化模型或是对数据进行压缩，同时最大程度的保持了原有数据的信息，最后的结果只与数据有关。各主成分之间正交，可以消除原始数据成分间对的影响。但是PCA是基于线性变换，假设数据是线性相关的。对于非线性关系较强的数据，PCA可能不够有效，需要使用非线性降维方法。

4.2参考书籍

《机器学习》周志华

《机器学习实战》 Peter Harrington