一、题目

二、题目分析
这是一个求直线旋转生成曲面方程的问题。对于这种问题,我有两种方法。
(1)公式快捷法
如果旋转轴是x/y/z,我们这里假设是z,且我们知道直线方程F(y,z)=0,那我们直接写出曲面方程:=0.
就是绕哪根轴旋转,那根轴不变,剩下的变成平方+另一个未知数平方根号的形式。
例如,直线绕z轴旋转一周的曲面方程为:
,就是把y变为了根号下x平方+y平方。
(2)通解法
这个解法可以求所有的直线,不仅仅是绕着坐标轴之一旋转。上面的解法也是从这个通解里推出来的。下面是我们简略的草图。s是旋转轴的方向向量,M0是旋转轴上一点,M1是已知直线上任意一点,而P就是我们旋转之后的曲面上的任意点我们根据两个条件就可以求出曲面方程:
1、
2、
这两个条件都很好理解,接下来我们把这个方法应用到我们今天的题目里。

三、解法
由于是绕着z轴旋转,所以我们选定M0为(0,0,0),方向向量s为(0,0,1).
接下来我们设置直线上任意一点M1为(x1,y1,z1),P为(x,y,z),即曲面上任意一点。
带入条件(1),可知
带入条件二,可知(x-x1,y-y1,z-z1)·(0,0,1)=0,得到z=z1。然后我们要利用原方程,消去x1,y1,z1。
联立以上两式,我们得到,接下来我们要将x1和y1,代回原方程,用z表示x1和y1,这样我们就可以得到曲面方程。x1=αz1+p,y1=βz1+q,由于z=z1,所以
这就得到了旋转曲面的方程啦!但是这个题目还要再进一步,讨论参数对曲面形状的影响,这还要求我们熟悉几种常见的曲面方程,会判断曲面形状。
四、知识点补充
常见的曲面方程如下:
圆柱面:只含有两个参数,且映射为圆。类似x²+y²=a
椭球面
单叶双曲面
双叶双曲面
椭圆抛物面
双曲抛物面(马鞍面)
椭圆锥面

其实也不需要死记硬背,只需要分别令每一个变量为常数,查看映射面的形状,就能判断出曲面形状!只要知道有这些形状就好。
然后我们就可以开始根据参数判断形状啦!我们先来化简,尝试把式子化成(x-x0) ²+(y-y0)²+(z-z0)²=const的形状。
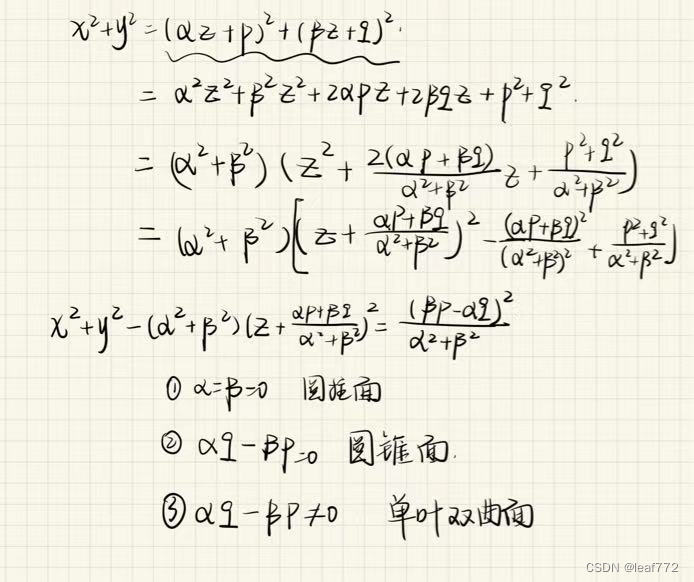























 3055
3055

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








