【考研数学每日题】直线与直线的关系

一、题目

二、题目分析

这道题考察的是根据直线和直线之间的关系求解直线方程。

我们首先需要知道，直线和直线有哪几种关系。然后我们要知道这几种关系怎么转化成数学表达式，这样我们才能求解。

1、直线之间的关系

垂直，平行，相交，异面、（重合）

一般不会考虑重合，但是本强迫症还是加上，给它一个括号算了。

2、关系的数学表达式

（1）垂直

这个很简单啦，就是方向向量的点积为零。

（2）平行

这个我们上次也说过了，就是方向向量成比例。

这里的（m1,n1,p1）（m2,n2,p2）就是方向向量，则。

但是！！！重合是平行的一个特例！我们需要考虑平行但是不重合的情况。

所以我们还需要加上一个条件。

我们在两条直线上各取一个点，分别为M1,M2,我们要求不平行于s1或者s2。这样我们就可以保证两直线不重合啦。

（3）相交

相交，我们可以想象一下，这两条直线在空间中一定是共面的！所以我们可以联想到上一道题目的混合积——共面的充要条件！！！

默念一百遍——相交，共面，相交，共面……

然后我们需要三个向量才能组成混合积，所以我们除了原本的两个方向向量之外，还要得到一个向量，就是我们上述的啦。

[,,]=0！

//插播一则小提醒，哔哔哔——请注意：

点积的结果和混合积的结果都是标量！只有叉乘的结果才是矢量！（因为混合积就是叉乘之后再点积，所以最后的结果形式和点积一致。）

//

（4）异面

异面，字面意思，就是不能构成一个平面，也就是相交的反面啦，混合积不等于零。

三、解法

好啦，我们取相交直线上的一个点（0，0，0），相交直线法向量（2，1，-1）.这个是从我们上次说的点向式方程里得出来的。

所以（1-0，2-0，1-0）和（2，1，-1）以及我们设出的要求的直线方向向量（m,n,p）的混合积为0.

得到m-n+p=0.

现在我们有了一个方向向量向量的约束条件啦，求出方向向量只需要两个约束条件，所以我们加上垂直的信息。（m,n,p）(3,2,1)=0

得到:3m+2n+p=0

联立约束条件：得到m=-3/5p,n=2/5p.

所以该支线方向向量为（-3，2，1）

//插播：方向向量是可以随意改变大小的，只要方向不变，即x,y,z的比例关系不变。所以我们可以任意缩放，即将x,y,z同时乘除一个数。

//

最后我们带入点向式方程，得到结果：

四、举一反三

（1）eg1

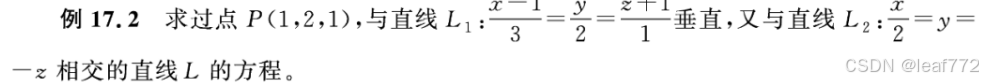
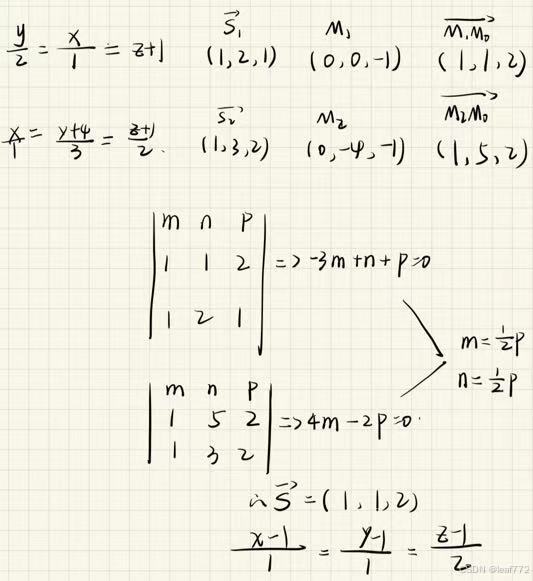
（2）eg2

这道题有四条交线，如果每条分别求混合积，很复杂。我们可以尝试换一种方法，比如设交点，而不是设直线的方向向量。

关于设置交点的方法，我们还可以延拓到eg1，因为有两个及以上的相交直线，就可以考虑此方法。以eg1为例，设交点分别为A,B。

噢，对了，这里我们补充一个直线的表达式，两点式。但是两点式本质上和点向式是一样的。因为分母的位置求的就是方向向量。

这个eg2我们也可以解出来，有两个解，分别是

五、总结

我们有两种方法求相交直线，一种是用混合积，另一种是设交点（已知两条及以上交线）。