【考研数学每日题】曲面与平面的关系

一、题目

二、题目分析

这道题要求的是椭球面与平面的关系。乍一看完全不知道从哪里下手，但是我们可以想象一下这三种关系在空间的表现，假设平面拉远拉近，靠近该椭球面。我们发现相切的条件就是平面和椭球面上最靠近它的一个点的距离的关系。那我们怎么求这个点呢？怎么求距离呢？答案就在于：这个点的切平面和平面Π平行。距离就是切平面和平面Π的距离。把曲面转换成平面，将曲面与平面关系转化成两个平面之间的关系之后，题目就似乎迎刃而解了。

1、切平面

首先我们要知道什么是切平面。我这里下一个简明的定义：曲面上一点的所有切线都在一个平面内，这个平面就是该切点的切平面。切平面的求解如下所示，（1）是曲面切平面的求解通式，（2）是我们得到的椭球面的方程。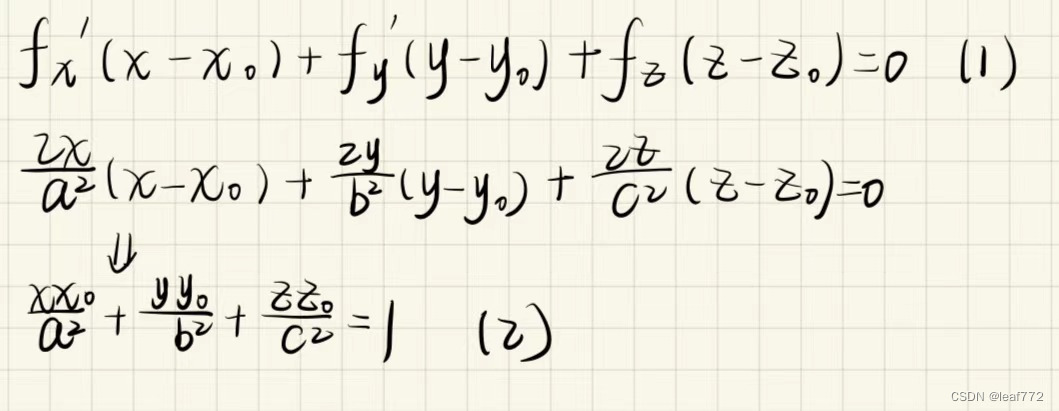  

那么对于椭球面，我们的切平面方程就是：

三、解法

首先我们设切点为M（x0,y0,z0），然后求出切平面方程，让切平面方程和平面平行，即成比例。

(t为随意正常数)

由于切点一定在椭球面上，所以我们把上述三个式子回代进椭球面的方程，得到

这样我们就求出了切平面的方程。

随后我们就开始求解距离问题。我们知道点到平面的距离公式是

以及由该式推出来的平面之间的距离公式：

可是在本题中，我们求两个平面之间的距离，会导致化简有些复杂，所以我们考虑把直接求两个平面的距离化为求两个平面到原点的距离的差。

切平面到原点的距离为：

已知平面到原点的距离为：

所以当t=1时，两距离相等，即为相切关系；

t>1时，d1<d2,为相离关系；

t<1时，为相交关系。