优化方法——梯度下降算法
1. 无约束最优化问题
1.1 梯度下降
1. 何为梯度下降:
- 梯度下降(Gradient Descent)是一个算法,但不是像多元线性回归那样是一个具体做回归任务的算法,而是一个非常通用的优化算法来帮助一些机器学习算法(都是无约束最优化问题)求解出最优解, 所谓的通用就是很多机器学习算法都是用梯度下降,甚至深度学习也是用它来求解最优解。
- 所有优化算法的目的都是期望以最快的速度把模型参数θ求解出来,梯度下降法就是一种经典的常用的优化算法。
2. 梯度下降的必要性:
- 利用正规方程求解的
θ
\theta
θ 的前提条件是损失函数是凸函数。但是,机器学习的损失函数并非都是凸函数,设置导数为 0 可能会得到很多个极值,不能确定唯一解。
- 使用正规方程 θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy 求解的另一个限制是特征维度( X 1 、 X 2 … … 、 X n X_1、X_2……、X_n X1、X2……、Xn)不能太多,因为矩阵逆运算的时间复杂度通常为 O ( n 3 ) O(n^3) O(n3) 。
- 也就是说,如果特征数量翻倍,你的计算时间大致为原来的 2 3 2^3 23 倍,也就是之前时间的8倍。举个例子,2 个特征 1 秒,4 个特征就是 8 秒,8 个特征就是 64 秒,16 个特征就是 512 秒,当特征更多的时候呢?计算过程会非常耗时。
- 所以正规方程求出最优解并不是机器学习甚至深度学习常用的手段。
3. 梯度下降的思想:
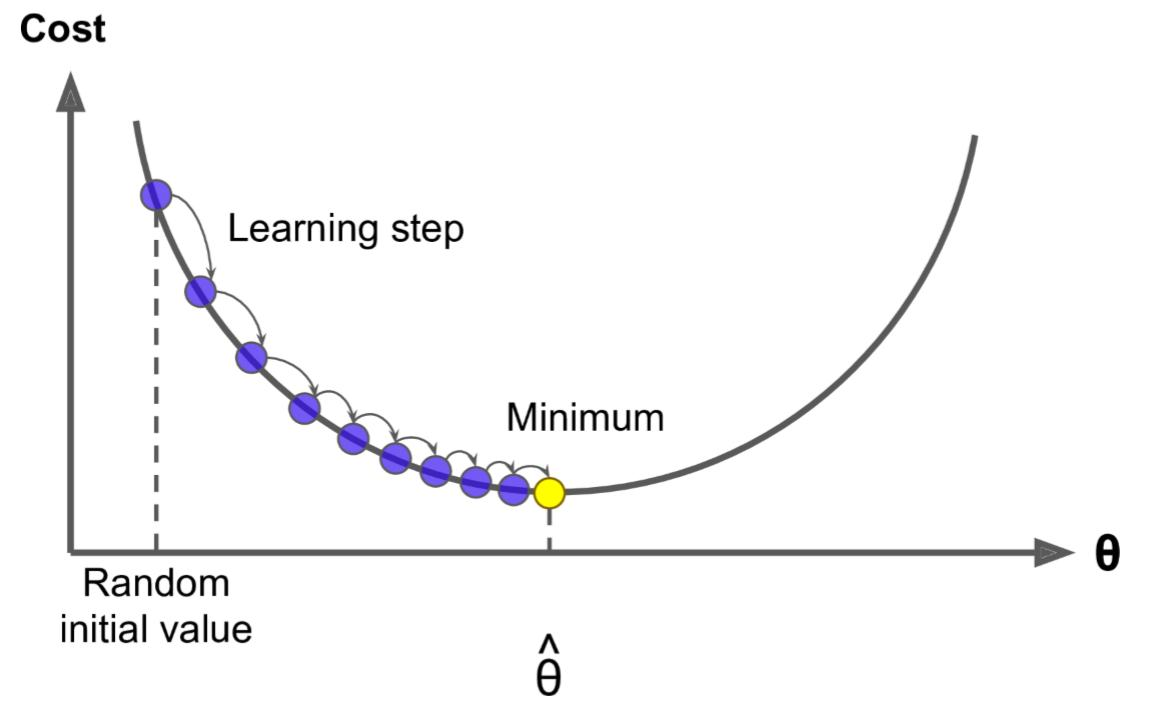
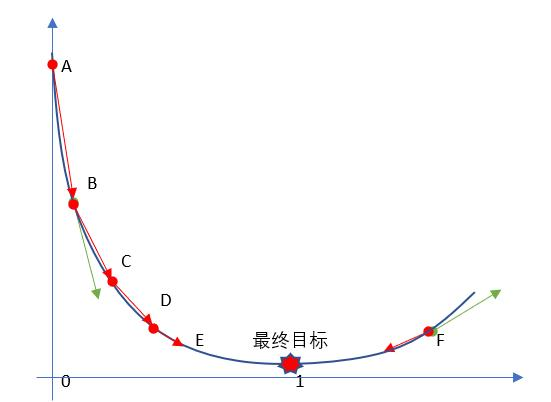
- 之所以叫梯度下降,是因为它的计算过程跟下山一样,每次都像坡度向下的方向走一小步,更新 θ \theta θ,直至找到最低点。
1.2 梯度下降公式
1. 公式:
-
梯度下降的更新公式,其实就是参数 θ \theta θ 的更新公式( θ \theta θ是一个参数向量, n n n 表示迭代次数):
- θ n + 1 = θ n − η ∗ g r a d i e n t \theta^{n + 1} = \theta^{n} - \eta * gradient θn+1=θn−η∗gradient
-
其中 η \eta η 表示学习率, g r a d i e n t gradient gradient 表示梯度:
- θ n + 1 = θ n − η ∗ ∂ L ( θ ) ∂ θ \theta^{n + 1} = \theta^{n} - \eta * \frac{\partial L(\theta)}{\partial \theta} θn+1=θn−η∗∂θ∂L(θ)
-
由于 θ = { θ 1 , θ 2 , . . . , θ m } \theta=\{\theta_1,\theta_2,...,\theta_m\} θ={θ1,θ2,...,θm} ,所以有:
- θ j n + 1 = θ j n − η ∗ ∂ L ( θ ) ∂ θ j ( j = 1 , 2 , . . . , m ) \theta_j^{n + 1} = \theta_j^{n} - \eta * \frac{\partial L(\theta)}{\partial \theta_j}(j=1,2,...,m) θjn+1=θjn−η∗∂θj∂L(θ)(j=1,2,...,m)
-
这里的 θ j \theta_j θj 就是 θ \theta θ 中的某一个具体的参数值( j = 1 , 2 , . . . , m j=1,2,...,m j=1,2,...,m,表示共有 m m m个属性,有 m m m个具体的参数 w w w需要确定),这里的 η \eta η 就是梯度下降图里的 learning step,也叫学习率 learning rate,很多时候也用 α \alpha α 表示,是我们自己设置的,属于超参。
-
可以把学习率 η \eta η 形象的看作是下山所迈的步子大小,步子迈的大,下山就快,但也不能太大(后面讲)。
2. 理解公式:
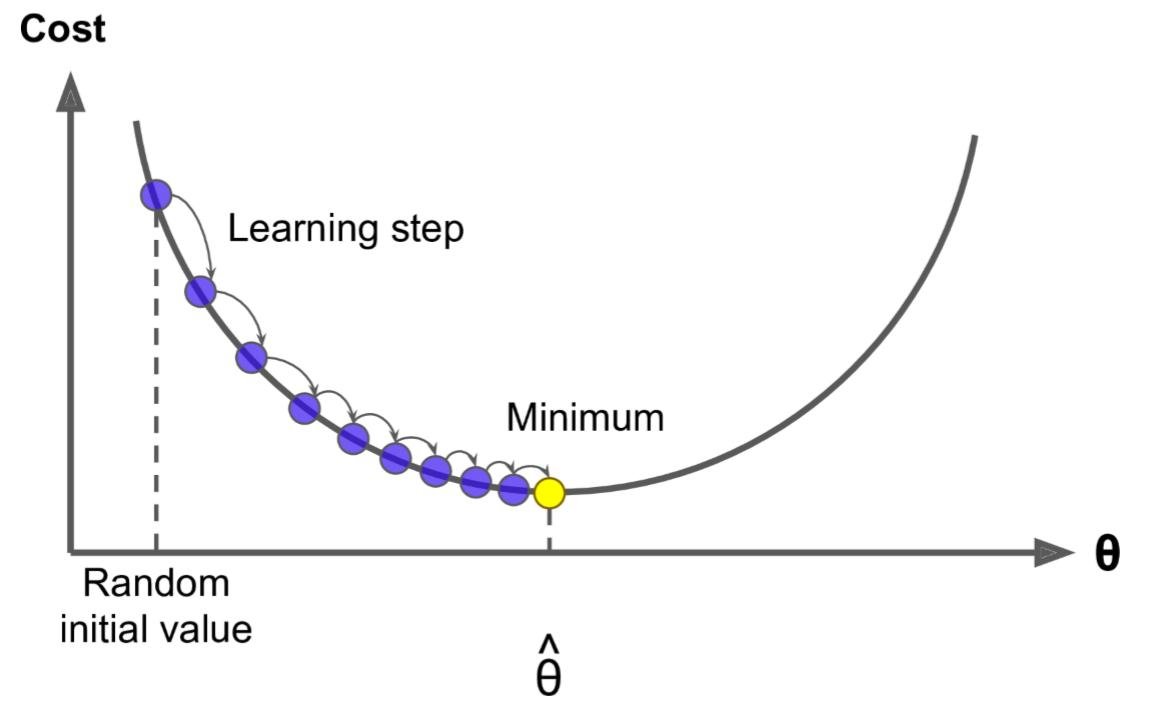
-
学习率 η \eta η 一般都是正数,如果在山左侧(曲线左半边)梯度(导数)是负的,那么 η ∗ g r a d i e n t \eta*gradient η∗gradient 就是负的, θ \theta θ 就会变大;如果在山右侧(曲线右半边)梯度就是正的,那么 η ∗ g r a d i e n t \eta*gradient η∗gradient 就是正的, θ \theta θ 就会变小。每次 θ \theta θ 调整的幅度就是 η ∗ g r a d i e n t \eta * gradient η∗gradient,也就是横轴上移动的距离(如果放在二维平面来说, θ \theta θ就是 x x x值)。
-
因此,无论在左边,还是在右边,梯度下降都可以快速找到局部最优解。
-
如果特征越多(也就意味着维度多),那么 θ j n + 1 = θ j n − η ∗ ∂ L ( θ ) ∂ θ j ( j = 1 , 2 , . . . , m ) \theta_j^{n + 1} = \theta_j^{n} - \eta * \frac{\partial L(\theta)}{\partial \theta_j}(j=1,2,...,m) θjn+1=θjn−η∗∂θj∂L(θ)(j=1,2,...,m)这个公式用的次数就越多,也就是每次迭代要应用的这个式子多次(多少特征,就应用多少次)。
-
所以其实上面的图不是特别准确(上图中, θ \theta θ为一维的),因为 θ \theta θ 对应的是很多维度,应该每一个维度都可以画一个这样的图,或者是一个多维空间的图。假设 θ \theta θ 维度为2,可画出一个三维图像:

- 观察上图我们不难发现,不是 θ 0 \theta_0 θ0 或 θ 1 \theta_1 θ1 其中一个方向上找到最小值就是最优解,而是所有方向上一起找到 L ( θ ) L(\theta) L(θ) 最小值才是最优解。
有些地方也把损失函数 L ( θ ) L(\theta) L(θ)写作 J ( θ ) J(\theta) J(θ)。
1.3 学习率
1. 学习率过大,过小的影响:
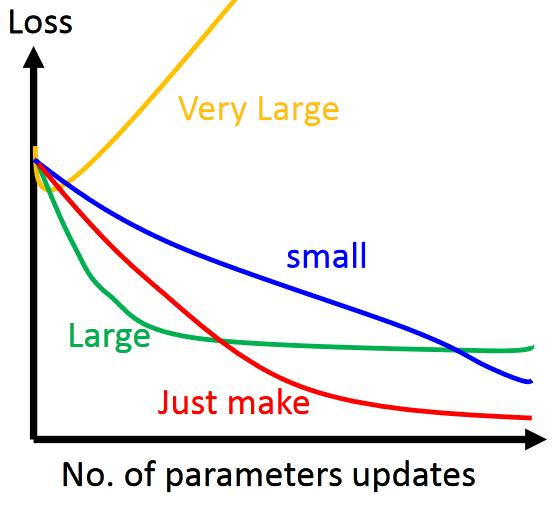
- 学习率大,可能一下子迈过了,到另一边去了(从曲线左半边跳到右半边),继续梯度下降又迈回来, 使得来来回回震荡,可能无法收敛;
- 步子太小呢,就像蜗牛一步步往前挪,虽然一定会收敛,但会使得整体迭代次数增加。
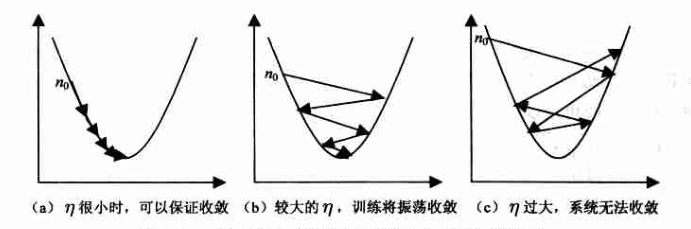
2. 学习率的设置:
- 学习率的设置是门一门学问,一般我们会把它设置成一个比较小的正整数,0.1、0.01、0.001、0.0001,都是常见的设定数值(然后根据情况调整)。
- 一般情况下学习率在整体迭代过程中是不变,但是也可以让学习率随着迭代次数的增多不断变小,因为越靠近山谷我们就可以步子迈小点,可以更精准的走入最低点,同时防止走过。
- 还有一些深度学习的优化算法会自己控制调整学习率这个值。
1.4 全局最优化
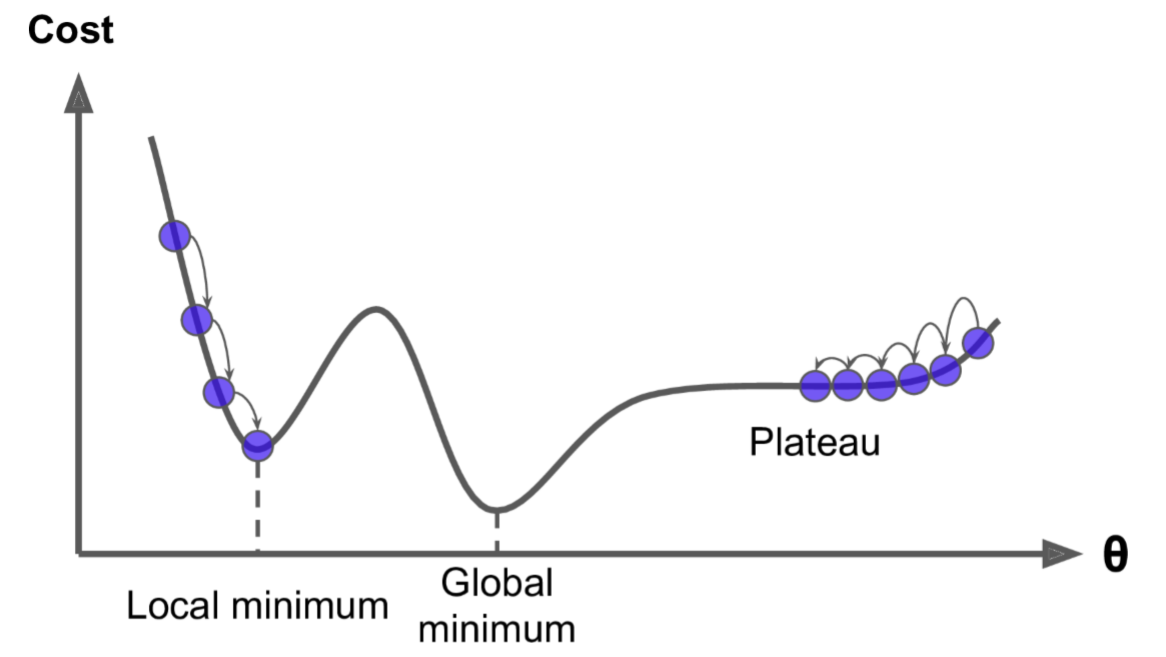
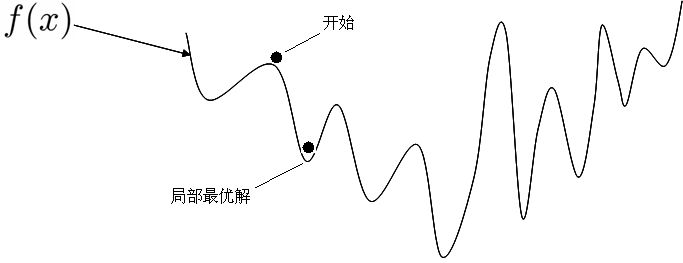
上图显示了梯度下降的两个主要挑战:
- 若随机初始化,算法从左侧起步,那么会收敛到一个局部最小值,而不是全局最小值;
- 若随机初始化,算法从右侧起步,那么需要经过很长时间才能越过Plateau(函数停滞带,梯度很小),如果停下得太早,则永远达不到全局最小值;
而线性回归的模型MSE损失函数恰好是个凸函数,凸函数保证了只有一个全局最小值,其次是个连续函数,斜率不会发生陡峭的变化,因此即便是乱走,梯度下降都可以趋近全局最小值。
上图损失函数是非凸函数,梯度下降法是有可能落到局部最小值的,所以其实步长不能设置的太小太稳健,那样就很容易落入局部最优解。虽说局部最小值也没太大问题, 因为模型只要是可以用的就好,但是我们还是要尽量奔着全局最优解去!
1.5 梯度下降步骤
梯度下降流程就是“猜”正确答案的过程:
- (1)先“瞎蒙”一些数,用Random给 θ \theta θ 一些初始值,随机生成一组数据 θ 0 , θ 1 , . . . , θ m \theta_0,\theta_1,...,\theta_m θ0,θ1,...,θm。最好是期望 μ \mu μ 为0,方差 σ \sigma σ 为1的正态分布数据。
- (2)求梯度 g g g,梯度代表曲线某点上的切线斜率,沿着切线往下,就相当于沿着坡度最陡的方向下降。
- (3)判断是否收敛(convergence),如果收敛跳出迭代,如果没有达到收敛,回第2步再次执行2~3步;或定义一个迭代次数,不用判断是否收敛,循环执行第2步,达到规定迭代次数后,自动跳出循环。
- 收敛的判断标准是:随着迭代进行,损失函数Loss变化非常微小,甚至不再改变,即认为达到收敛。
1.6 代码模拟梯度下降
1. 要求解的方程如下:
f
(
x
)
=
(
x
−
3.5
)
2
−
4.5
x
+
10
f(x) = (x - 3.5)^2 - 4.5x + 10
f(x)=(x−3.5)2−4.5x+10
2. 函数可视化:
import matplotlib.pyplot as plt
import numpy as np
# 目标函数
f = lambda x: (x - 3.5) ** 2 - 4.5 * x + 10
# 导函数
g = lambda x: 2 * (x - 3.5) - 4.5
# 函数可视化
x = np.linspace(0, 11.5, 100)
y = f(x)
plt.plot(x, y)
plt.show()
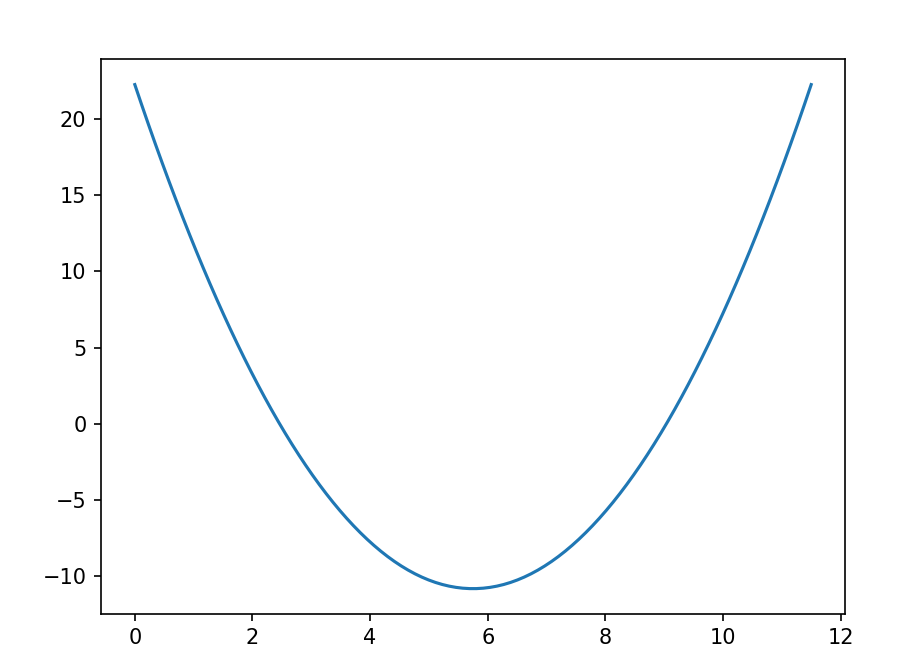
3. 使用正规方程求解:
# 求导函数,令导函数为0,求解最小值对应的x值
# 2 * (x - 3.5) - 4.5 = 0
# 得 x = 5.75
4. 使用梯度下降求解:
- 某些情况下,方程过于复杂(非凸函数,或特征数太多),不适合用正规方程求解。
eta = 0.1 # 学习率
x = np.random.randint(0, 12, size=1)[0] # 瞎蒙一个随机的初始值,x就是theta
# 之后的梯度下降中,会while循环多次更新x,last_x就是某一次x更新前的值
last_x = x + 0.1 # 加0.2也可以,只是为了让last_x和x有差异
precision = 0.0001 # 精确度
print('随机的x是:', x)
while True:
if np.abs(x - last_x) < precision: # 更新时,x几乎不再变化,可以终止了
break
last_x = x # 记录更新之前的x
x = x - eta * g(x) # 套更新公式
print('更新后的x是:', x)
- 输出:
随机的x是: 9
更新后的x是: 8.35
更新后的x是: 7.83
更新后的x是: 7.414
更新后的x是: 7.0812
更新后的x是: 6.81496
更新后的x是: 6.601968
更新后的x是: 6.431574400000001
更新后的x是: 6.29525952
更新后的x是: 6.186207616
更新后的x是: 6.0989660928
更新后的x是: 6.0291728742399995
更新后的x是: 5.973338299391999
更新后的x是: 5.9286706395136
更新后的x是: 5.89293651161088
更新后的x是: 5.8643492092887035
更新后的x是: 5.841479367430963
更新后的x是: 5.82318349394477
更新后的x是: 5.808546795155816
更新后的x是: 5.796837436124653
更新后的x是: 5.787469948899722
更新后的x是: 5.779975959119778
更新后的x是: 5.773980767295822
更新后的x是: 5.769184613836658
更新后的x是: 5.765347691069326
更新后的x是: 5.762278152855461
更新后的x是: 5.759822522284368
更新后的x是: 5.757858017827495
更新后的x是: 5.756286414261996
更新后的x是: 5.7550291314095965
更新后的x是: 5.754023305127677
更新后的x是: 5.753218644102142
更新后的x是: 5.752574915281714
更新后的x是: 5.752059932225371
更新后的x是: 5.751647945780297
更新后的x是: 5.751318356624237
更新后的x是: 5.75105468529939
更新后的x是: 5.750843748239512
更新后的x是: 5.7506749985916095
更新后的x是: 5.750539998873288
更新后的x是: 5.75043199909863
更新后的x是: 5.750345599278904
- 最后得到的结果为5.750345599278904,这个结果已经非常接近准确答案了。
5. 注意:
- 梯度下降存在一定误差,不是完美解;
- 在误差允许的范围内,梯度下降所求得的机器学习模型,是可以使用的;
- 梯度下降的学习率 η \eta η,不能太大,否则无法收敛;
- 精确度,可以根据实际情况调整;
while循环退出条件是:x更新之后和上一次相差绝对值小于特定精确度。
2. 梯度下降方法
2.1 三种梯度下降方法
1. 梯度下降的分类:
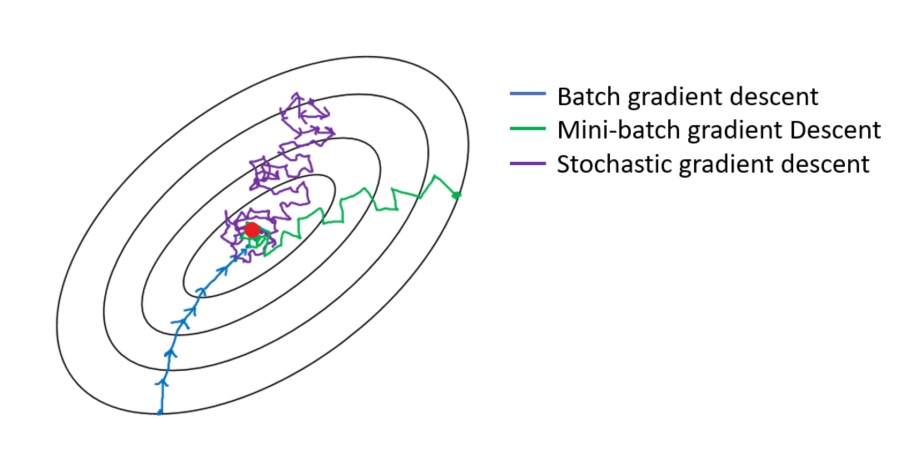
- 梯度下降分三类:批量梯度下降BGD(Batch Gradient Descent)、小批量梯度下降MBGD(Mini-Batch Gradient Descent)、随机梯度下降SGD(Stochastic Gradient Descent)。
2. 回顾梯度下降步骤:
- (1)先“瞎蒙”一些数,用Random给 θ \theta θ 一些初始值,随机生成一组数据 θ 0 , θ 1 , . . . , θ m \theta_0,\theta_1,...,\theta_m θ0,θ1,...,θm。最好是期望 μ \mu μ 为0,方差 σ \sigma σ 为1的正态分布数据。
- (2)求梯度 g g g,梯度代表曲线某点上的切线斜率,沿着切线往下,就相当于沿着坡度最陡的方向下降。
- (3)判断是否收敛(convergence),如果收敛跳出迭代,如果没有达到收敛,回第2步再次执行2~3步;或定义一个迭代次数,不用判断是否收敛,循环执行第2步,达到规定迭代次数后,自动跳出循环。
- 收敛的判断标准是:随着迭代进行,损失函数Loss变化非常微小,甚至不再改变,即认为达到收敛。
3. 三种梯度下降不同,体现在第二步中:
-
BGD是指在每次迭代使用所有样本来进行梯度的更新;
-
MBGD是指在每次迭代使用一部分样本(例如所有样本500个,使用其中32个样本)来进行梯度的更新;
-
SGD是指每次迭代随机选择一个样本来进行梯度更新。
2.2 线性回归梯度更新公式
1. 线性回归的损失函数
- 求和写法:
L ( θ ) = 1 2 ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 L(\theta) = \frac{1}{2}\sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) - y^{(i)})^2 L(θ)=21i=1∑n(hθ(x(i))−y(i))2 - 矩阵写法:
L ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) L(\theta) = \frac{1}{2}(X\theta - y)^T(X\theta - y) L(θ)=21(Xθ−y)T(Xθ−y)
2. 推导 θ \theta θ 的更新公式
-
最原始的 θ \theta θ 更新公式为:
θ j n + 1 = θ j n − η ∗ ∂ L ( θ ) ∂ θ j \theta_j^{n + 1} = \theta_j^{n} - \eta * \frac{\partial L(\theta)}{\partial \theta_j} θjn+1=θjn−η∗∂θj∂L(θ) -
但是我们并不知道损失函数的导数,所以需要将 ∂ L ( θ ) ∂ θ j \frac{\partial L(\theta)}{\partial \theta_j} ∂θj∂L(θ) 推导出来:
- = ∂ ∂ θ j 1 2 ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 = \frac{\partial}{\partial \theta_j}\frac{1}{2}\sum \limits_{i=1}^{n}(h_{\theta}(x^{(i)}) - y^{(i)})^2 =∂θj∂21i=1∑n(hθ(x(i))−y(i))2
- = 1 2 ∗ 2 ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) ∂ ∂ θ j ( h θ ( x ( i ) − y ( i ) ) ) =\frac{1}{2}*2\sum \limits_{i=1}^{n}(h_{\theta}(x^{(i)})-y^{(i)})\frac{\partial}{\partial \theta_j}(h_{\theta}(x^{(i)}-y^{(i)})) =21∗2i=1∑n(hθ(x(i))−y(i))∂θj∂(hθ(x(i)−y(i)))
- = ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) =\sum \limits_{i=1}^{n}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} =i=1∑n(hθ(x(i))−y(i))xj(i)
-
总结:
- θ j n + 1 = θ j n − η ∗ ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta * \sum \limits_{i=1}^{n}(h_{\theta}(x^{(i)}) - y^{(i)})x_j^{(i)} θjn+1=θjn−η∗i=1∑n(hθ(x(i))−y(i))xj(i)
大家记不住推导过程,或者不理解,也不强求,只需要记住最后的结论(总结)即可。
2.3 批量梯度下降BGD
1. BGD的思想:
- 批量梯度下降法是最原始的形式,它是指在每次迭代使用所有样本来进行梯度的更新。
2. 每次迭代参数的更新公式:
- 每一个参数值的更新:
θ j n + 1 = θ j n − η ∗ 1 n ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *\frac{1}{n}\sum\limits_{i = 1}^{n} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗n1i=1∑n(hθ(x(i))−y(i))xj(i) - 有些地方也喜欢将
1
n
\frac{1}{n}
n1 和
η
\eta
η 合并,直接写成:
θ j n + 1 = θ j n − η ∗ ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *\sum\limits_{i = 1}^{n} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗i=1∑n(hθ(x(i))−y(i))xj(i) - 参数向量的更新公式,矩阵写法(此处
X
X
X是样本全集):
θ n + 1 = θ n − η ∗ X T ( X θ − y ) \theta^{n + 1} = \theta^{n} - \eta * X^T(X\theta -y) θn+1=θn−η∗XT(Xθ−y)
矩阵写法中,我们引入了偏置项,即吸入 b b b。将一列1,放在了数据集的最前面,即 x 0 ( i ) = 1 x_0^{(i)}=1 x0(i)=1。
这里也是,只需要记住最重要的矩阵写法即可,推导过程实在记不住不强求。
3. 优点:
- 一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行;
- 由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向逼近。
4. 缺点:
- 当样本数目 n n n 很大时,每迭代一步都需要对所有样本进行计算,训练过程会很慢。
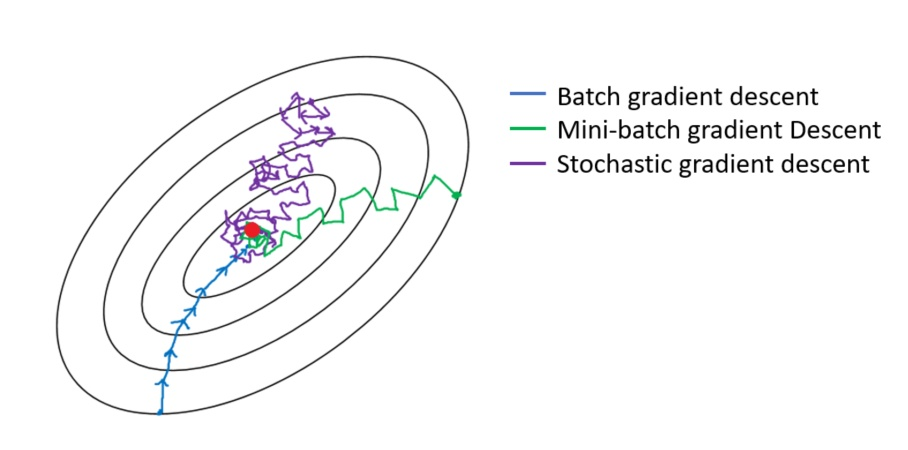
5. 从迭代的次数上来看,BGD迭代的次数相对较少:
- 对应下图蓝色的线,每一步都比较精准。
2.4 随机梯度下降SGD
1. SGD的思想:
- 随机梯度下降法不同于批量梯度下降,每次迭代仅使用一个样本来对参数进行更新。
2. 参数更新公式:
- 每一个参数值的更新公式:
θ j n + 1 = θ j n − η ∗ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *(h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗(hθ(x(i))−y(i))xj(i) - 矩阵写法,参数向量的更新公式(此处
X
X
X中只有随机的一个样本):
θ n + 1 = θ n − η ∗ X T ( X θ − y ) \theta^{n + 1} = \theta^{n} - \eta * X^T(X\theta -y) θn+1=θn−η∗XT(Xθ−y)
3. 优点:
- 由于不是在全部训练数据上进行更新计算,而是在每轮迭代中,随机选择一条数据进行更新计算,这样每一轮参数的更新速度大大加快。
4. 缺点:
- 每一次下降的准确度下降。因此即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
- 可能会收敛到局部最优,因为单个样本并不能代表全体样本的趋势。
5. 解释一下为什么SGD收敛速度比BGD要快:
- 这里我们假设有30W个样本,对于BGD而言,每次迭代需要计算全部的30W个样本才能对参数进行一次更新,需要求得最小值可能需要多次迭代(假设这里是10次)。
- 而对于SGD,每次更新参数只需要一个样本,因此若使用这30W个样本进行参数更新,则参数一次训练会被迭代30W次,而这期间,SGD就可能保证收敛到一个合适的最小值上了。
- 也就是说,上面的例子中,在收敛时,BGD计算了 10×30W 次,而SGD只计算了 1×30W 次。
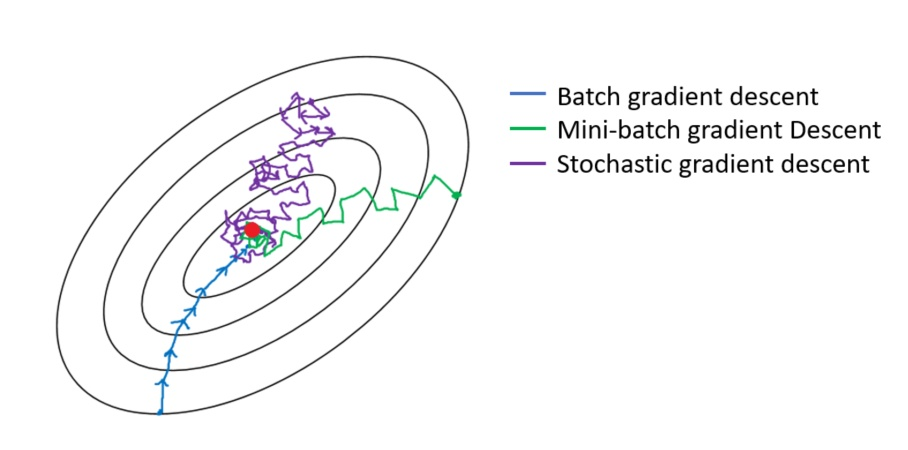
6. 从迭代的次数上来看,SGD迭代的次数较多,搜索过程就会盲目一些:
- 对应紫色的曲线。
2.5 小批量梯度下降MBGD
1. 思想:
- 小批量梯度下降,是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是:每次迭代使用总样本中的一部分(batch_size)样本来对参数进行更新。这里我们假设 batch_size = 20,样本数 n = 1000 。实现了更新速度与更新次数之间的平衡。
2. 参数的更新公式:
- 每个参数值的更新公式:
θ j n + 1 = θ j n − η ∗ 1 b a t c h _ s i z e ∑ i = 1 b a t c h _ s i z e ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *\frac{1}{batch\_size}\sum\limits_{i = 1}^{batch\_size} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗batch_size1i=1∑batch_size(hθ(x(i))−y(i))xj(i) - 矩阵写法(此处 X X X是全集中的一部分样本):
θ n + 1 = θ n − η ∗ X T ( X θ − y ) \theta^{n + 1} = \theta^{n} - \eta * X^T(X\theta -y) θn+1=θn−η∗XT(Xθ−y)
3. MBGD的优势:
-
相对于随机梯度下降算法,小批量梯度下降算法降低了收敛波动性, 即降低了参数更新的方差,使得其更新更加稳定。
-
相对于BGD,其提高了每次学习的速度。并且不用担心内存瓶颈,从而可以利用矩阵运算进行高效计算。
-
一般情况下,小批量梯度下降是梯度下降的推荐变体,特别是在深度学习中。每次随机选择2的幂数个样本来进行学习,例如:8、16、32、64、128、256。因为计算机的结构就是二进制的。但是也要根据具体问题而选择,实践中可以进行多次试验, 选择一个使更新速度与更次次数都较适合的样本数。
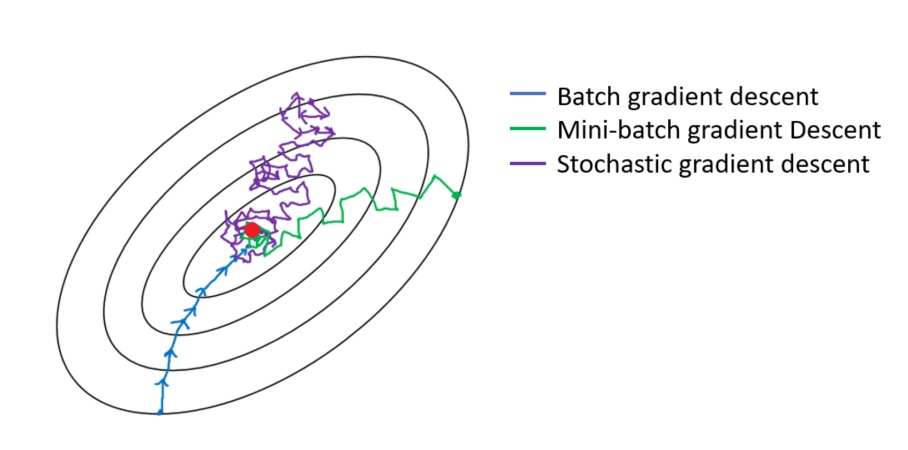
4. MBGD梯度下降迭代的收敛曲线更加温柔一些:
- 对应绿色曲线。
2.6 梯度下降优化
1. 虽然梯度下降算法效果很好,并且广泛使用,但是不管用上面三种哪一种,都存在一些挑战与问题,我们可以从以下几点进行优化:
-
选择一个合理的学习速率很难。如果学习速率过小,则会导致收敛速度很慢。如果学习速率过大,那么其会阻碍收敛,即在极值点附近会振荡。
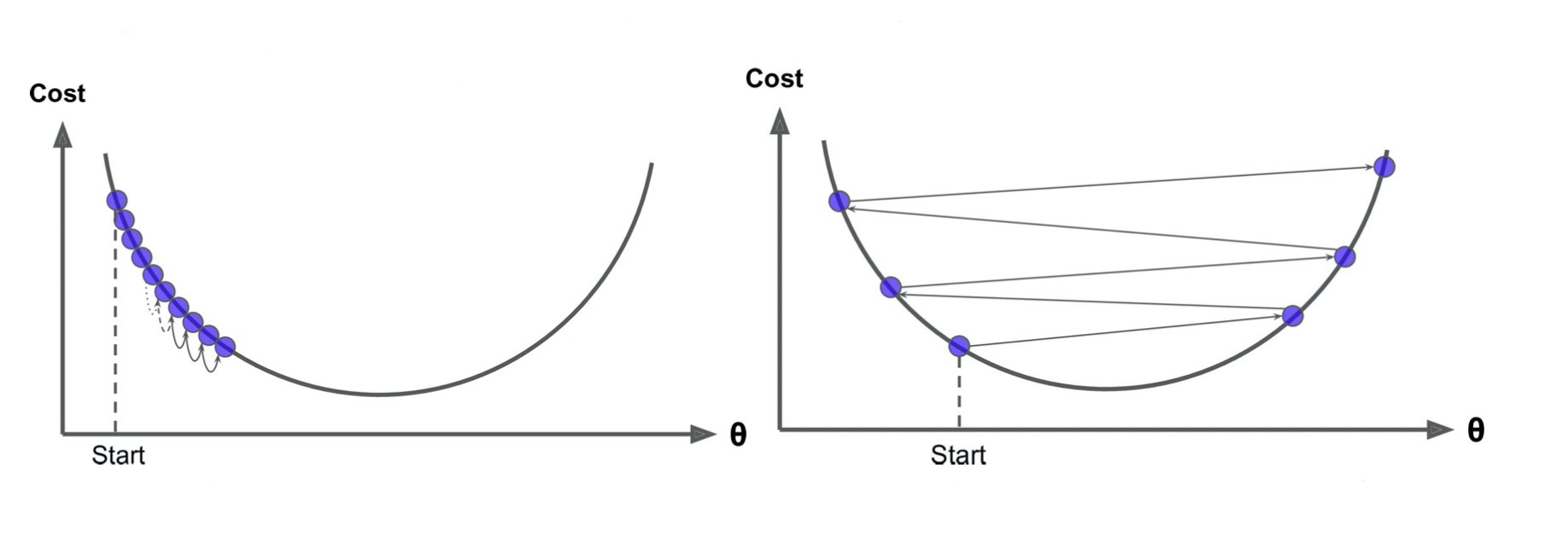
-
学习速率调整,试图在每次更新过程中, 改变学习速率。从经验上看,学习率在一开始要保持大些来保证收敛速度,在收敛到最优点附近时要小些以避免来回震荡。比较简单的学习率调整可以通过 学习率衰减——Learning Rate Decay的方式来实现。假设初始化学习率为 η 0 \eta_0 η0,在第 t 次迭代时的学习率 η t \eta_t ηt。常用的衰减方式为可以设置为按迭代次数进行衰减,迭代次数越大,学习率越小!
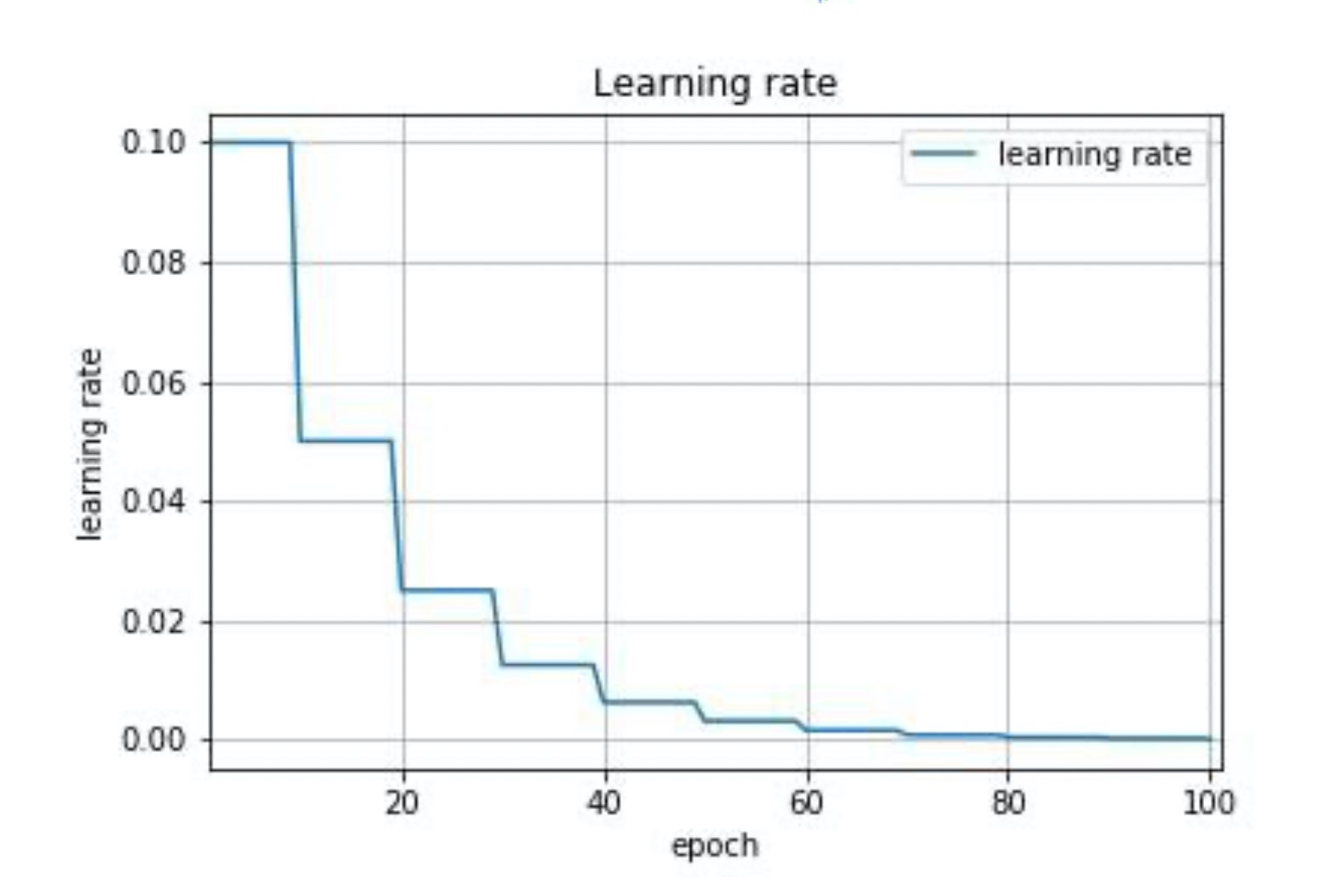
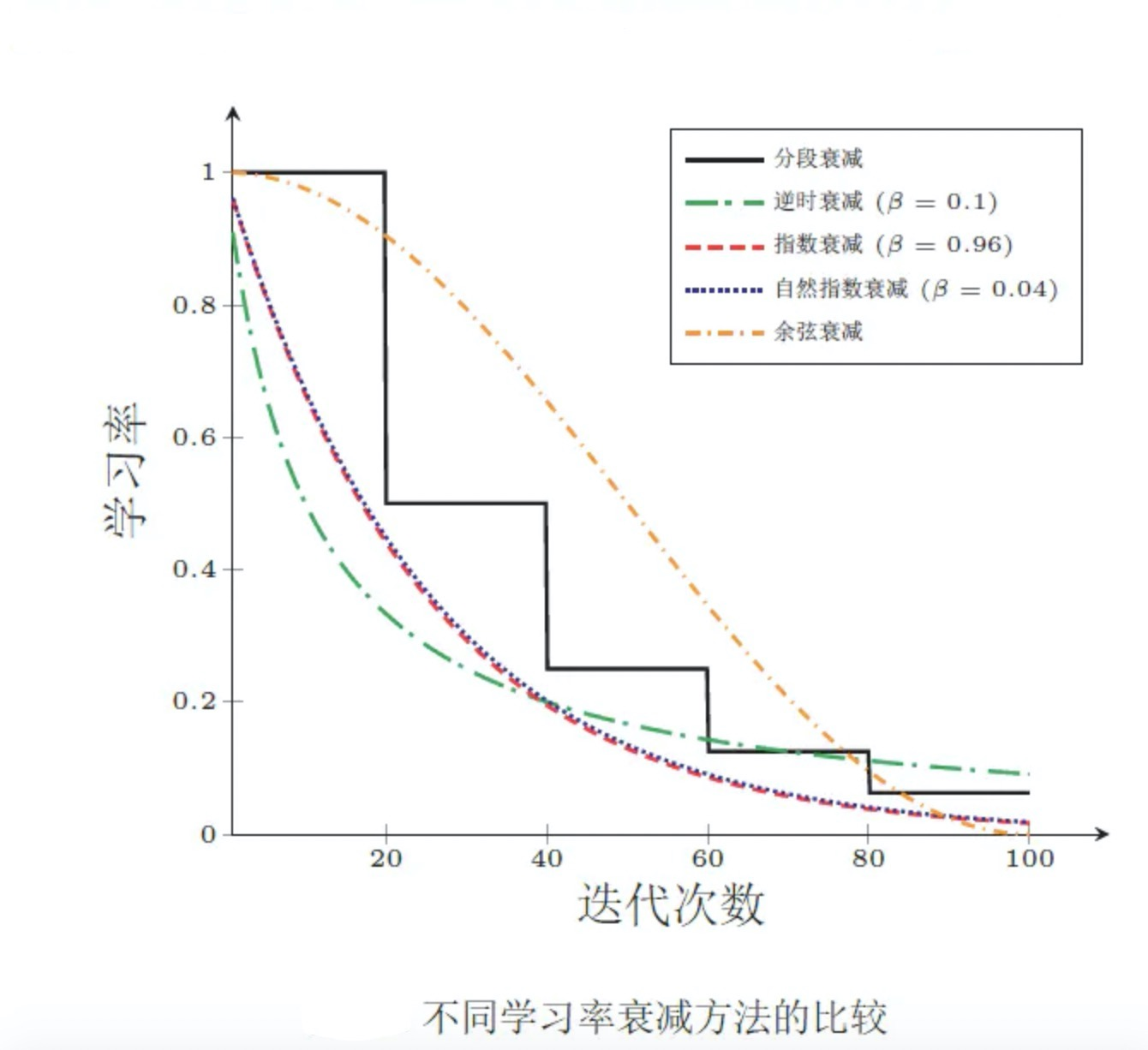
-
模型所有的参数每次更新都是使用相同的学习速率。如果数据特征是稀疏的,或者每个特征有着不同的统计特征与空间,那么便不能在每次更新中每个参数使用相同的学习速率,那些很少出现的特征应该使用一个相对较大的学习速率。
-
对于非凸目标函数,容易陷入那些次优的局部极值点中,如在神经网路中。
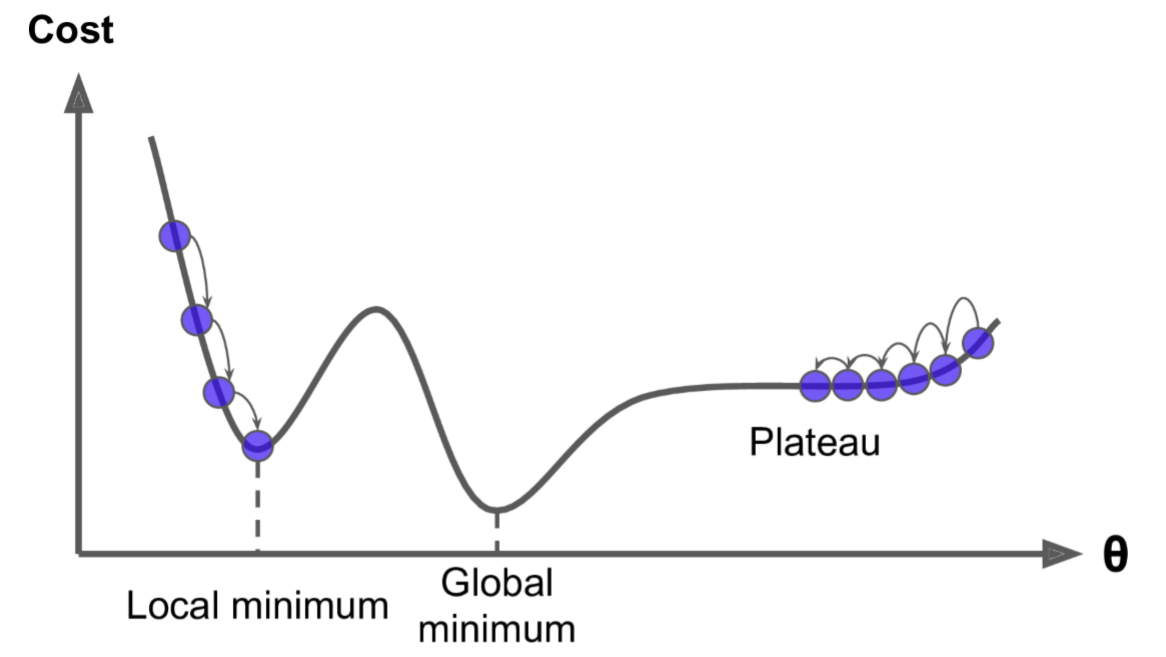
简单的问题,一般使用随机梯度下降即可解决。在深度学习里,对梯度下降又进行了很多改进,比如:自适应梯度下降。
2. 轮次和批次:
-
轮次:epoch,轮次顾名思义,是把我们已有的训练集数据学习多少轮,迭代多少次。
-
批次:batch,这里指的的我们已有的训练集数据比较多的时候,一轮要学习的数据太多, 那就把一轮次要学习的数据分成多个批次,一批一批数据的学习。(好比背课文时,一段一段的背)
-
在进行机器学习,模型训练时,要合理选择轮次和批次。
3. 代码实战
3.1 BGD代码实战
1. 一元一次线性回归:
import numpy as np
import matplotlib.pyplot as plt
# 一元一次线性回归
"""准备数据"""
X = np.random.rand(100, 1)
w, b = np.random.randint(1, 10, size=2)
# 增加噪声,使其更像真实数据
y = w * X + b + np.random.randn(100, 1)
plt.scatter(X, y)
plt.show()
# 将b吸入矩阵
X = np.concatenate([X, np.full(shape=(100, 1), fill_value=1)], axis=1) # 将b放在了最后一列
"""开始训练"""
# 循环次数
epochs = 10000
# 逆势衰减,随着梯度下降次数增加,调整学习率使其变小
def learning_rate_shedule(t):
# t 为当前迭代次数
return 5 / (t + 1000) # 初始时学习率为 0.005
# 要求解的系数
theta = np.random.randn(2, 1) # 系数一般都是列向量
for i in range(epochs):
# 批量梯度下降,X包含所有数据
g = X.T.dot(X.dot(theta) - y)
# 学习率
eta = learning_rate_shedule(i)
theta = theta - eta * g
print('真实的斜率和截距是:', w, b)
print('BGD求解的斜率和截距是:', theta)
2. 多元一次线性回归:
import numpy as np
# 多元一次线性回归
X = np.random.rand(100, 8) # 随机生成100行8列的数据
w = np.random.randint(1, 10, size=(8, 1))
b = np.random.randint(1, 10, size=1)
y = X.dot(w) + b + np.random.randn(100, 1)
# 将b吸入矩阵
X = np.concatenate([X, np.full(shape=(100, 1), fill_value=1)], axis=1) # 将b放在了最后一列
# 循环次数
epochs = 10000
# 逆势衰减,随着梯度下降次数增加,调整学习率使其变小
def learning_rate_shedule(t):
# t 为当前迭代次数
return 5 / (t + 1000) # 初始时学习率为 0.005
# 要求解的系数
theta = np.random.randn(9, 1) # 系数一般都是列向量
for i in range(epochs):
# 批量梯度下降,X包含所有数据
g = X.T.dot(X.dot(theta) - y)
# 学习率
eta = learning_rate_shedule(i)
theta = theta - eta * g
print('真实的斜率和截距是:', w, b)
print('BGD求解的斜率和截距是:', theta)
3.2 SGD代码实战
1. 一元一次线性回归:
import numpy as np
# 一元一次线性回归
"""准备数据"""
X = np.random.rand(100, 1)
w, b = np.random.randint(1, 10, size=2)
# 增加噪声,使其更像真实数据
y = w * X + b + np.random.randn(100, 1)
# 引入偏置项
X = np.concatenate([X, np.full(shape=(100, 1), fill_value=1)], axis=1)
"""开始训练"""
epochs = 100
# 逆势衰减,随着梯度下降次数增加,调整学习率使其变小
def learning_rate_shedule(t):
# t 为当前迭代次数
return 5 / (t + 1000) # 初始时学习率为 0.005
# 要求解的系数
theta = np.random.randn(2, 1) # 系数一般都是列向量
for t in range(epochs):
# 每轮迭代开始前,打乱样本顺序
index = np.arange(100) # 0~99
np.random.shuffle(index) # 洗牌,打乱索引顺序
X = X[index]
y = y[index]
for i in range(100): # 从100个数据中随机拿一个训练
X_i = X[[i]] # 注意有两个[],保证X_i为二维数组
y_i = y[[i]]
g = X_i.T.dot(X_i.dot(theta) - y_i)
eta = learning_rate_shedule(t) # 学习率
theta = theta - eta * g
print('真实的斜率和截距是:', w, b)
print('BGD求解的斜率和截距是:', theta)
2. 多元一次线性回归:
import numpy as np
# 多元一次线性回归
"""准备数据"""
X = np.random.rand(100, 8)
w = np.random.randint(1, 10, size=(8, 1))
b = np.random.randint(1, 10, size=1)
# 增加噪声,使其更像真实数据
y = X.dot(w) + b + np.random.randn(100, 1)
# 引入偏置项
X = np.concatenate([X, np.full(shape=(100, 1), fill_value=1)], axis=1)
"""开始训练"""
epochs = 100
# 逆势衰减,随着梯度下降次数增加,调整学习率使其变小
def learning_rate_shedule(t):
# t 为当前迭代次数
return 5 / (t + 1000) # 初始时学习率为 0.005
# 要求解的系数
theta = np.random.randn(9, 1) # 系数一般都是列向量
for t in range(epochs):
# 每轮迭代开始前,打乱样本顺序
index = np.arange(100) # 0~99
np.random.shuffle(index) # 洗牌,打乱索引顺序
X = X[index]
y = y[index]
for i in range(100):
X_i = X[[i]] # 注意有两个[],保证X_i为二维数组
y_i = y[[i]]
g = X_i.T.dot(X_i.dot(theta) - y_i)
eta = learning_rate_shedule(t) # 学习率
theta = theta - eta * g
print('真实的斜率和截距是:', w, b)
print('BGD求解的斜率和截距是:', theta)
3.3 MBGD代码实战
直接上多元一次线性回归:
import numpy as np
X = np.random.randn(100, 8)
w = np.random.randint(1, 10, size=(8, 1))
b = np.random.randint(1, 10, size=1)
# 增加噪声
y = X.dot(w) + b + np.random.randn(100, 1)
# 引入偏置项
X = np.concatenate([X, np.ones((100, 1))], axis=1)
# 创建超参数轮次、样本数量、小批量数量
epochs = 10000
n = 100 # 样本数量
batch_size = 16 # 小批量样本数量
num_batches = int(n / batch_size) # 小批量数量
# 逆势衰减,随着梯度下降次数增加,调整学习率使其变小
def learning_rate_shedule(t):
# t 为当前迭代次数
return 5 / (t + 1000) # 初始时学习率为 0.005
# 要求解的系数
theta = np.random.randn(9, 1) # 系数一般都是列向量
for t in range(epochs):
# 每轮迭代开始前,打乱样本顺序
index = np.arange(100) # 0~99
np.random.shuffle(index) # 洗牌,打乱索引顺序
X = X[index]
y = y[index]
for i in range(num_batches):
# 一次取一批数据16个样本
X_batch = X[i * batch_size: (i + 1) * batch_size]
y_batch = y[i * batch_size: (i + 1) * batch_size]
g = X_batch.T.dot(X_batch.dot(theta) - y_batch)
eta = learning_rate_shedule(t)
theta = theta - eta * g
print('真实的斜率和截距是:', w, b)
print('BGD求解的斜率和截距是:', theta)























 1035
1035

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










