计算机图形学入门games103——fvm体积有限元

本质上线性有限元和体积有限元是等价的

如果说我将两个物体接触的面设为L，在上面单位面积所受到的力设做t，那么整个面所收到的合力就是整个面对于t的积分

那么表面的f可以写为法向量和应力矩阵的乘积

那么将其放入三角形中怎么认识呢，我们将x_0作为一个面的代表，那么对于周围单独的每一个三角形都有对其的作用力，此时我们并不知道怎么计算L，因此需要使用微积分的定量，将其转化为负的应力对相邻两个边的积分之和，因为L和另外两个边是一个封闭的图像，积分总和一定为0，这里取中点的原因是假设每个三角形对三个点力的贡献是平均的

在三维的情况下，计算的原理是一样的，就是多了一个维度，因此此时是对面的积分，转化后的公式也就如下

三角形面积的计算，空间向量知识（两条边的叉乘除以2），norm法向量，叉乘处于叉乘的绝对值

最后得到的就是三个边的叉乘和应力的公式

那么怎么得到应力stress呢，注意这个应力和我们上一次所使用的应力是不一样的，在这里的解释是，之前我们在线性有限元中，能量是能量密度和面积的乘积，能量密度和strain的函数，而这个面积是原面积（reference），这个条件下我们所计算出的矩阵Stress是在reference条件下的

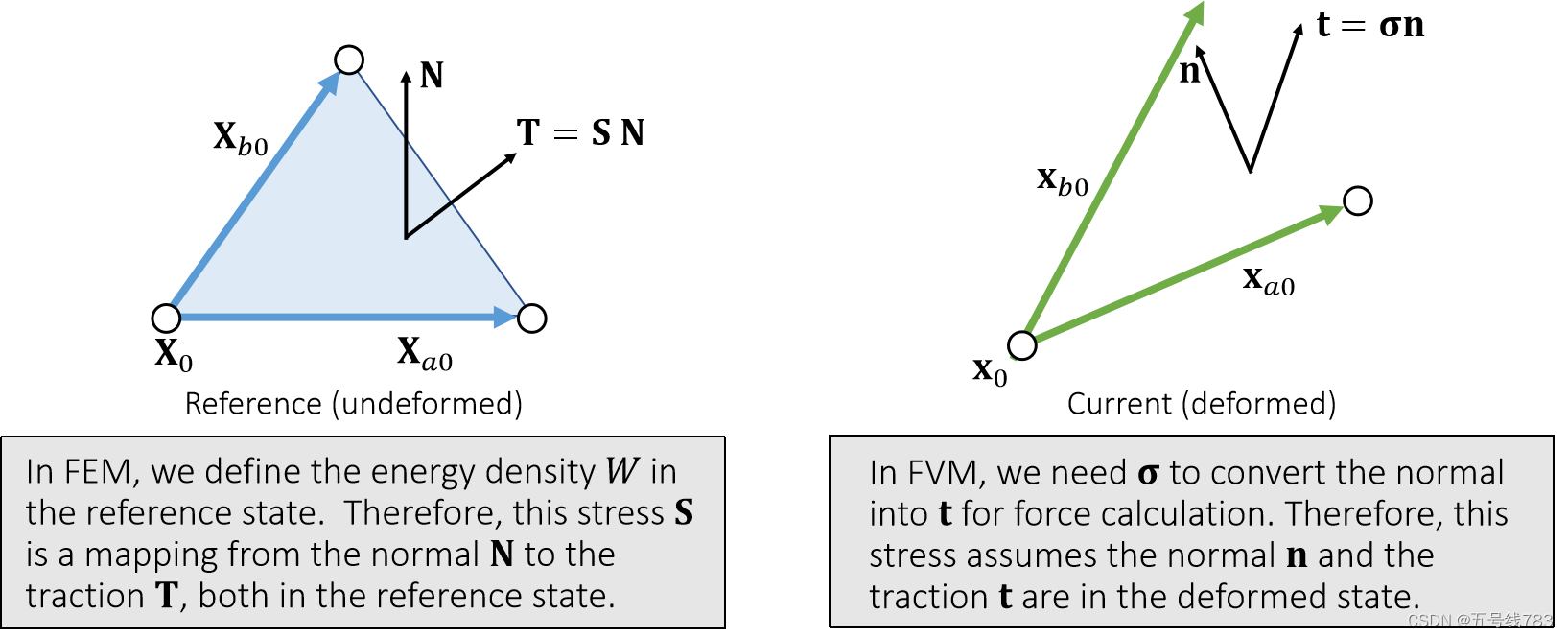
那么FVM中，我们假设出来的单位面积所受的力t和法向量n是在形变后的条件下的，因此两个stress是有区别的，我们在这种条件下怎么描述stress呢，那么有四种组合可能，其中常用的是三种，这节课我们使用的是柯西stress （Cauchy）

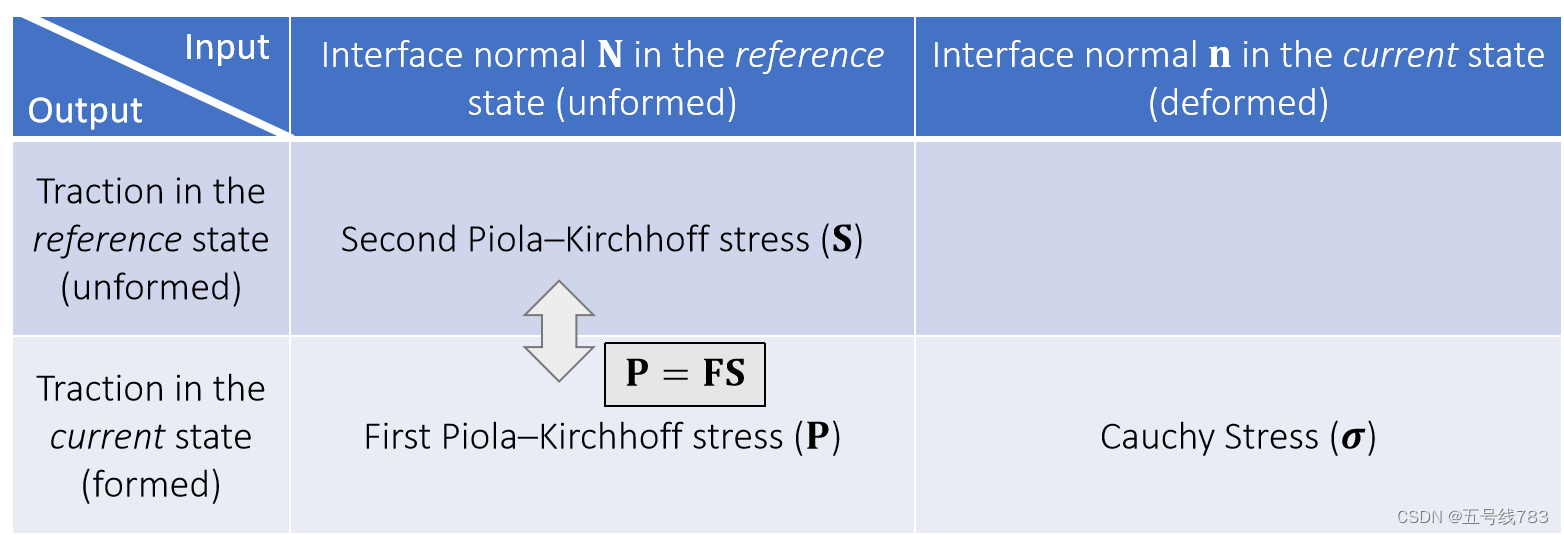
我们无法直接获取到柯西应力，但是第二皮耶罗应力在上次的fem中已知如何求解，就是能量密度对于应变的求导，而第二皮耶罗应力和第一皮耶罗应力乘以一个形变矩阵就可以转换，而第一皮耶罗应力和柯西应力之间有一个转化公式（过程省略，在paper中）

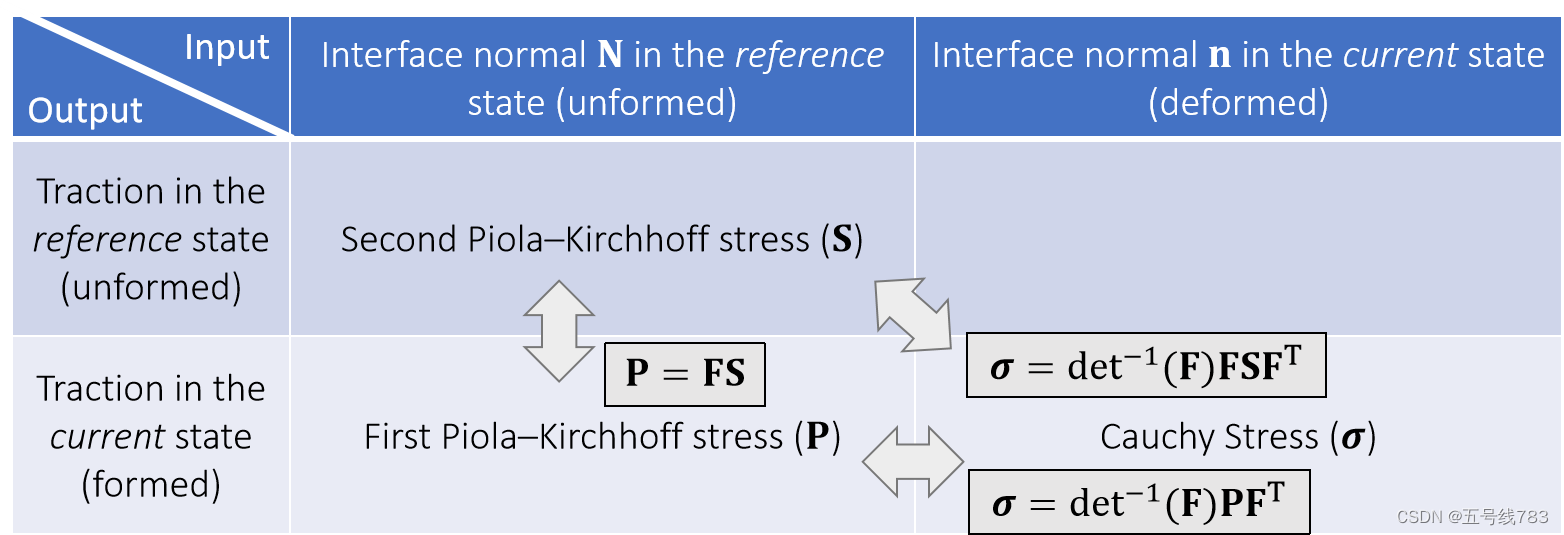
那么我们知道柯西应力是把形变后的应力写为形变后的Norm表达，而第一皮耶罗应力是形变后的应力写为形变前的Norm表达，那么norm是很容易计算的，而形变前的norm向量都是常数，简化了计算，用P = Fs，得到简化公式，而S可以根据FEM中的公式得出

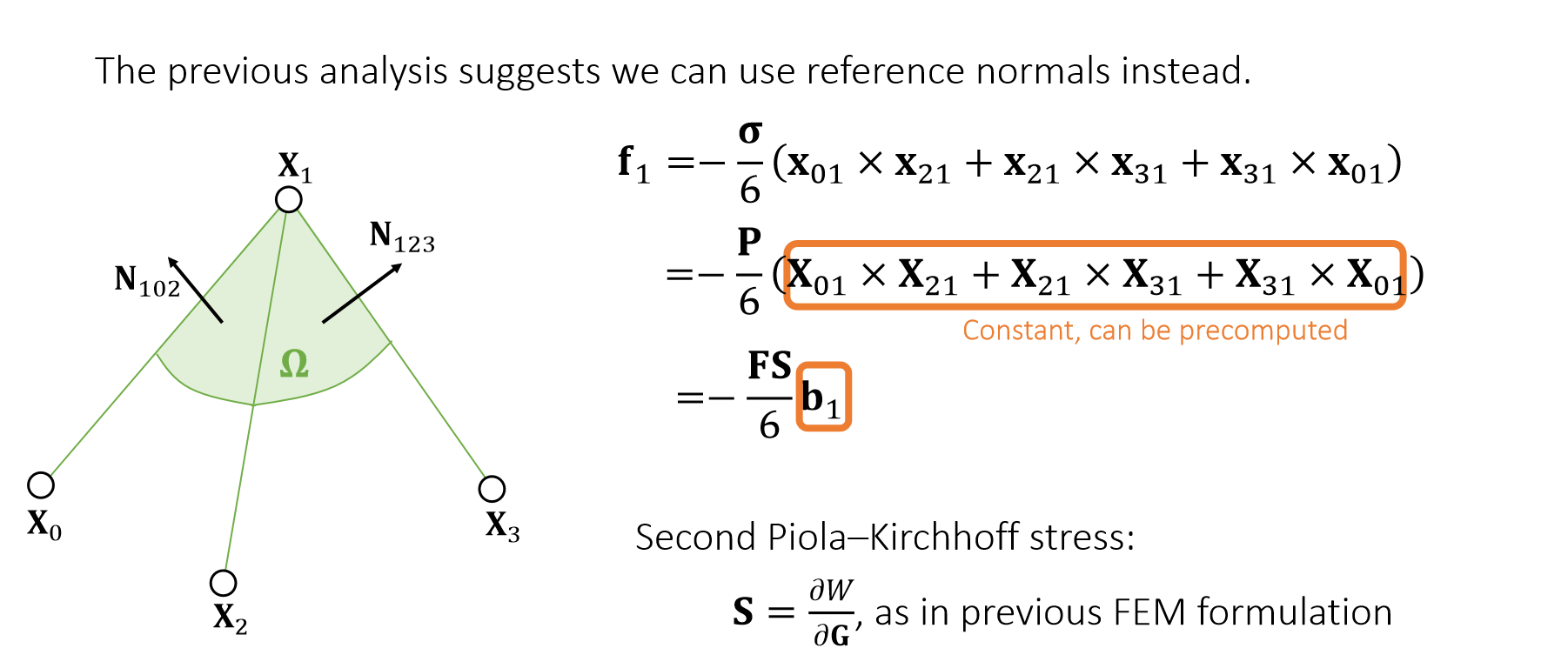
其中S的计算如下，FEM中推导

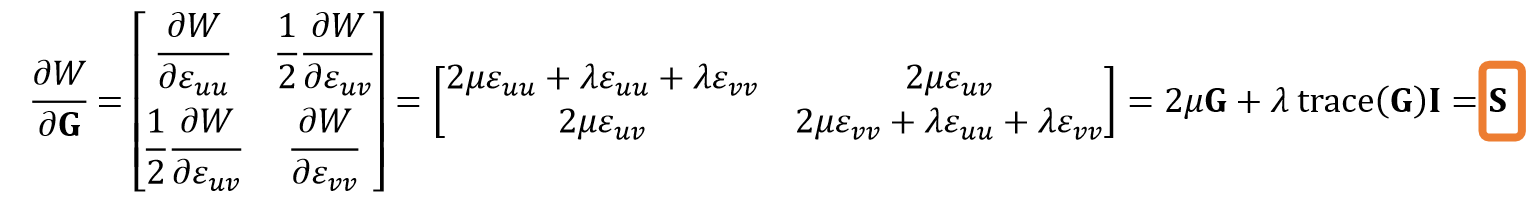
形变矩阵计算公式，也是在之前就有过推导

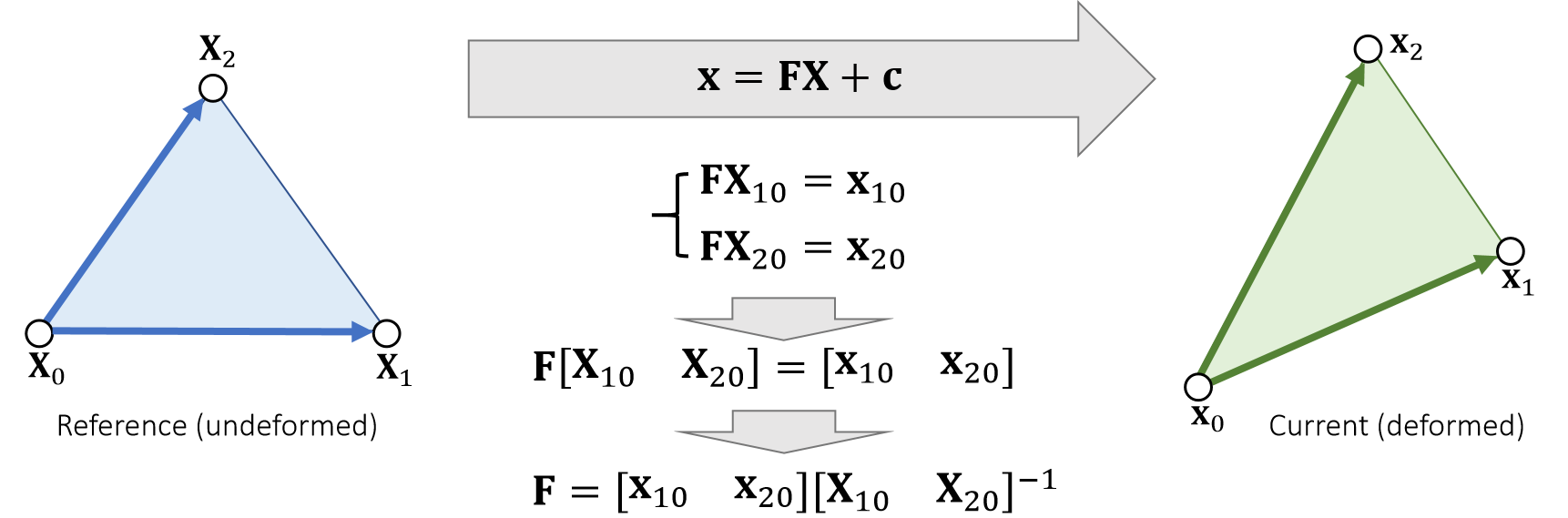
这些计算的选择逻辑是选择对计算最友好的方式，本质上几种应力的所做的工作都是映射，最后计算出的力都是等价的

关于b_1的更多思考

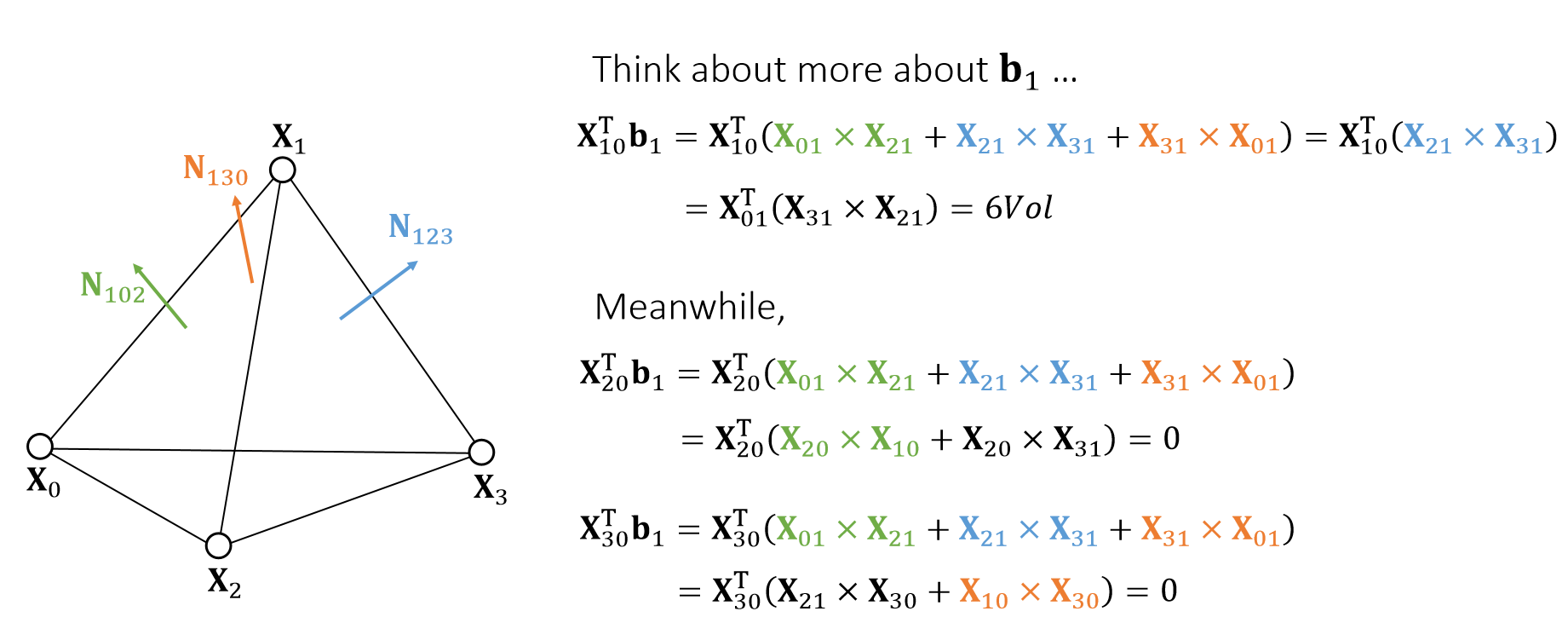
我们以此继续推导这些Norm，可以得到以下结论

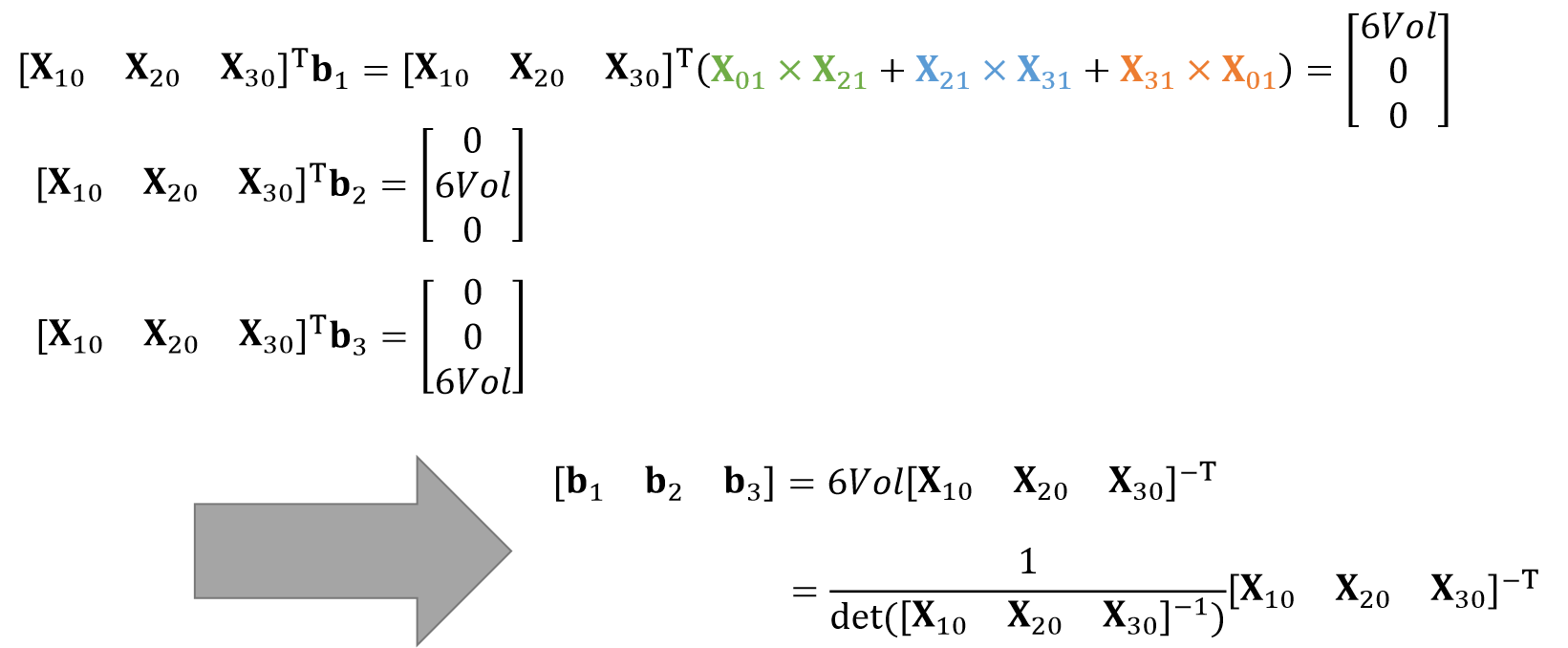
最后的伪代码

这个四面体是一个实心的四面体，不是一个空壳