数电实验：利用74ls00和74ls86实现全加器

目录

一、实验目的

二、实验内容

三、实验步骤、数据记录及处理

四、实验心得

---

 

一、实验目的

熟悉数字电路实验箱的使用，熟悉ttl系列门元件芯片的使用，能够利用分立元器件门电路，搭建特定组合逻辑电路。

二、实验内容

验证741s00和74ls86的功能，利用74ls00 和74ls86  实现1位全加器和全减器。

三、实验步骤、数据记录及处理

1.实验仪器的结构图

        74ls00是由4 组 俩输入的与非门所构成,7 脚GND接地,14脚VCC接+5V,其中1,2为输入端,3为输出端,4,5输入端,6为输出端,等

 

         74ls86是由4 组 俩输入的异或门所构成,7 脚GND接地,14脚VCC接+5V,其中1,2为输入端,3为输出端,4,5输入端,6为输出端,等

2.设计全加器

        在将三个多位二进制数相加时，除了最低位以外，每一位都考虑来自低位的进位，即将三个对应位的加数和来自低位的进位3个数相加。这种运算称为全加，所用的电路称为全加器。

          用异或门（74LS86）和与非门（74LS00）组成全加器，并测试全加器的逻辑功能。

设计方法：

1. 分析电路图

 

函数表达式:

Si = A ⨁B⨁C;

Ci+1 = (A⨁B)C + AB;

 

 

 

2.根据二进制加法运算规则列出1位全加器的真值表。

 

 

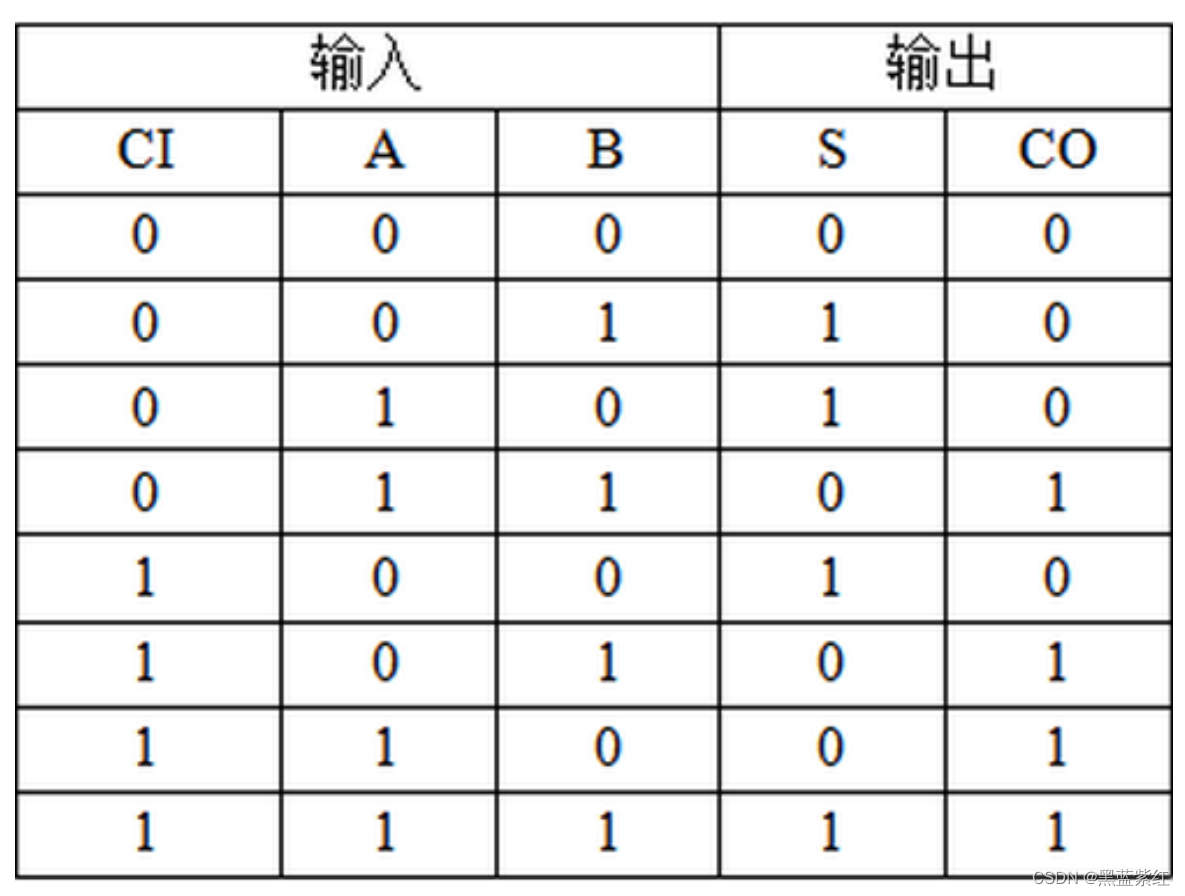
3.实验电路的设计图:    三位全加器

 

 

四、实验心得

        在进行实验时，应先确认74LS00、74LS86的功能完好，而后仔细检查芯片的引脚连接，确保连接正确，以避免电路故障。

        实验有助于加深对异或门和与非门对电路设计的理解，同时也提供了一个实际的编程和模拟测试经验。为了更好地理解电路的运作，我们可以尝试设计更复杂的电路或改进现有的设计。实验中要确保安全，特别是在使用电源和连接线时，避免短路和电击风险。

 

                                 （ 看到这儿，老铁不来个  一键三连，支持支持）

                                              多多重复,百炼成钢

                                    相信今天的讲解会使你学会这道题！！！