高中信息技术python及答案,信息技术必修一python

最新推荐文章于 2024-07-22 06:44:14 发布

wenangou

最新推荐文章于 2024-07-22 06:44:14 发布

阅读量425

点赞数

文章标签：算法 java

本文链接：https://blog.csdn.net/wenangou/article/details/132734447

版权

本文详细介绍了高中信息技术教材中关于Python版本的多项式函数及其求值方法，重点讲解了秦九韶算法的原理和Python实现步骤，包括多项式输入、数学输出和求值函数QJS_Poly及其扩展版QJS_Poly_ex的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

大家好，小编为大家解答高中信息技术新教材中python版本的问题。很多人还不知道高中信息技术 python 教学内容，现在让我们一起来看看吧！

3.2.3 求值的秦九韶算法实现QJS_Poly(f,x)

3.2.4 秦九韶算法扩展版QJS_Poly_ex(f,x)

1、多项式函数

关于x的一元多项式，它有很多非常直观的函数表达F(x)。

$F(x)=x+1$

$F(x)=x^{2}+2x-2$

$F(x)=4x^{3}+2x^{2}-9x+1$

$F(x)=2x^{10}-3x^{8}-5x^{6}+x^{3}+8x^{2}+x+1$

你可以用函数、方程、代数式之间的关系去理解多项式、多项式求值、多项式函数、一元高次多项式等不同表述神码ai火车头伪原创插件怎么用【php源码】。

2、多项式函数求值

当我们创建好条件，规避掉风险，十载寒窗数据收集，邀请发小数学家小明、物理学家小东、生物学家小强三宵两夜彻夜分析，穷究古今中外理论之大成辛辛苦苦描绘出函数后，函数求值将显得那么光芒万丈、熠熠生辉，如日临大地般指引我们昂首前进。

那么，对于任意给定的一个关于x的n次多项式，如何求任一x的函数值？

以 $F(x)=4x^{3}+2x^{2}-9x+1$ 为例，这样求F(2)不香吗？

那这样呢？

前方高能。

真香，还可以是这样！

我们当下的知识当然是博大精微，拥有的计算工具形形色色，多项式求值那是轻轻松松两三秒搞定，可古时候的人们计算方法很有限，自然是拒绝各种其他香。

那么，那时候的算法对我们还有意义吗？这个，你觉得有那就有，你觉得没有那就没有，我们都可以做回大爷。我还是比较认为有的。

3、一元高次多项式求值的秦九韶算法实现

我们有了一种手工计算一元高次多项式求值的新途径。

3.1 秦九韶算法

秦九韶算法的数学表示：

简单分析一下其过程。在对多项式进行一定的处理后，让“ax+b”这一步骤在不断迭代、重复中进行n次后，就可以求出f(x)。很明显，上述过程是基于 $a_{n}$ ， $a_{n-1}$ ， $a_{n-2}$ ，…， $a_{1}$ 都不为0的F(x)。如果对F(x)的输入处理得当，系数为不为0都可以。

3.2 秦九韶算法的python实现

完成整个求值过程很简单：构造并输出多项式函数，指定x求值，输出结果。

3.2.1 多项式的输入In_F

def In_F():
    f=[]
    print("=======================================================================")
    print("请输入多项式各项的系数a与对应次数n，尽量按降幂排列，结束时请输入系数0")
    while True:#每次输入多项多函数中的一项：系数，对应未知数的次数
           a=int(input("请输入当前项系数a="))
           if(a==0):
               break;
           n=int(input("请输入当前项次数,常数项为0，n="))
           f.append([n,a]) #次数在前，系数在后
    f.sort()#按次数从小到大排序
    i=j=0
    n=max(f)[0]
    #构造完整的n次多项式函数，不考虑同类项等特殊情形，已输入的项数小于等于n+1，i为各项下标：a0到an
    #用for i in range(n+1)也可以，但是对于有删除操作的情形会有下标越界的风险
    while i<=n:
        if(i==0):
            if(f[i][0]!=0):#没有常数项时构造常数项a0。不存在项定义：有未知数的次数但系数为0
                f.insert(i,[0,0])
        elif(f[i][0]!=f[j][0]+1):#相邻项的次数应依次减1
            f.insert(i,[f[j][0]+1,0])
        j=i
        i+=1
    f.sort(reverse=True)  #用数学中熟悉的降幂排列表示
    print("=======================================================================")
    return f

下图是F(x)的逻辑结构，物理上通过嵌套list实现。每一个元素存放多项式一个项的系数与指数。

程序中对多项式进行处理，使不存的项以系数为0、指数为0的项出现，整个F(x)按降幂排列。

3.2.2 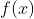$f(x)$ 的数学输出Out_F(f)

这个函数对于整个秦九韶算法的实现来说可有可无，仅用于将 $f(x)$ 从一种数据结构输出为我们熟悉的数学形式。

def Out_F(f):
    print("F(x)=",end="")
    n=len(f)
    for i in range(n):
        if(f[i][1]==0):
            continue
        if(f[i][0]==0 and f[i][1]!=0):#输出常数项
            print("%+d"%f[i][1],end="")
            continue
        if(abs(f[i][1])!=1):
            if(i==0):
                print("%dx"%f[i][1],end="")
            else:
                print("%+dx"%f[i][1],end="")
        else:
            if(f[i][1]>0):
                if(i==0):
                    print("x",end="")
                else:
                    print("+x",end="")
            else:
                print("-x",end="")
        if(f[i][0]!=1):
            print("^%d"%f[i][0],end="")
    print()

Out_F(f)在输出过程中主要解决的问题有±1系数输出、正负系数符号输出、0指数输出、1指数输出等。总之，尽可能使 $f(x)$ 的输出形式符合我们数学上的书写习惯。

$F(x)=x+1$

$F(x)=x^{2}+2x-2$

$F(x)=2x^{10}-3x^{8}-5x^{6}+x^{3}+8x^{2}+x+1$

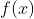3.2.3 $f(x)$ 求值的秦九韶算法实现QJS_Poly(f,x)

def QJS_Poly(f,x):
    n=max(f)[0]
    s=f[0][1]*x+f[1][1]
    for i in range(1,n):
        s=s*x+f[i+1][1]
    return s

真正的算法实现非常简单，这就是计算机程序与人工相比真正的优势所在：自动且快速地进行大规模的重复处理。

第二个F(1)=9是另一个扩展版本输出的结果。

之前说过，这里在应用秦九韶算法解决求值问题的时候，In_F()会将没有输入的项，即 $a_{n}$ 、 $a_{n-1}$ 直到 $a_{1}$ 、 $a_{0}$ 中为0的项加入F(x)的逻辑结构中去，从而完整地应用秦九韶算法。

3.2.4 秦九韶算法扩展版QJS_Poly_ex(f,x)

如果不做扩充，那么该怎么应用秦九韶算法？

对于像 $f(x)=5x^{6}+x^{3}-x+1$ 这样的F $f(x)$ ，还能直接用秦九韶算法吗？答案其实非常简单，只要我们能理解秦九韶算法求解多项式的值的原理所在，就可以做类似处理，把原来的“ax+b”变为“ $ax^{m}$ +b”即可，如：

$f(x)=5x^{6}+x^{3}-x+1$

$=5x^{6}+x^{3}-x+1$

$=(5x^{5}+x^{2}-1)\cdot x+1$

$=((5x^{3}+1)x^{2}-1)x+1$

def QJS_Poly_ex(f,x):
    lf=[]
    while(len(f)>0):
        n=len(f)-1
        if(f[n][1]==0): #去掉构造时存在但实际上不存在的项
            f.pop()
        else:
            lf.append([f[n][0],f[n][1]])
            t=f.pop()
            i=0
            while(i<len(f)): #每提一次公因式，多项式函数中当前项的前面各项未知数次数应作调整，为后面的计算做准备
                f[i][0]-=t[0]
                i=i+1
    lf.reverse() #调整成降幂排列
    s=lf[0][1]*(x**lf[0][0])
    n=len(lf)
    for i in range(1,n):
        s=(s+lf[i][1])*(x**lf[i][0])  #和原来的秦九韶算法略有不同
    return s

在程序对按降幂排列的F(x)从右到左（也即从常数项到最高次项）进行处理后，lf列表存放各非零系数项的系数以及在提取 $x^{m}$ 后对应的指数，为后面的算法实现做好准备。