基础
两者的基础都是 求解特征值、特征向量
矩阵对向量的乘法,其实是矩阵对此向量的旋转和拉伸。
如果矩阵对某个向量V只拉伸而不旋转,那么V就是该矩阵的eigenVector,拉伸比就是eigenValue.
PCA
是对一个维度的分析,比如对features分析,可以实现特征降维。
SVD
A = U Σ V T A=U\Sigma V^T A=UΣVT
sigma: 奇异值矩阵
是对两个维度的分析。
比如矩阵的每行是产品,每列是用户,矩阵元素是评分。
可以使用SVD向用户做产品推荐。
U:表征的是输入
V:表征的是输出
在train阶段,可由A矩阵求出
U
U
U,
Σ
\Sigma
Σ,
V
V
V 三个矩阵。
在test阶段,对于新的
A
A
A, 可以使用已经计算好的U,Sgima,计算
V
=
A
T
U
Σ
−
1
V = A^T U \Sigma^{-1}
V=ATUΣ−1。注意此处的U可以只取前k列,Sigma值只取前k个。
比如:
A: 10*5,每一列是一个用户 共5个用户,每一行是产品 共10个产品,矩阵中数值是评分
U: 10*10,取前k列,=> (10,k)
Sigma: 10*5,取前k个奇异值,=> (k,k)
V: 5*5
test:
ai: 10*1,是一列,即此用户对10个产品的评分
vi = (1 * 10)(10 * k)(k * k) = (1 * k) ,可以理解为降维后的k个值 在坐标系的位置
把vi 放到坐标系里,使用余弦相似度 度量,找到最近邻(最近邻的喜好类似)。然后用最近邻的喜好产品向a用户推荐。
比如在坐标系里 Anna和Beta很近,使用余弦距离,
Beta对10个产品的评分:[9,9,5,1,6,9,9,…]
Anna的是: [9,9,0,0,0,9,9,…]
那么可以向Anna推荐 第5个、第3个产品。
求解步骤
- 求v
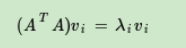
- 求u

- 求sigma

SVD作用
-
有降维、节约存储空间的效果,
若A维度是: (10000行, 1000列)。消耗空间:10000 * 1000 = 10^7 = 10,000,000
取K=100时,
U: (10000, 100), 消耗:10^6
Sigma: (100, 100), 消耗:10^4
VT: (100, 1000), 消耗: 10^5
消耗求和:1,110,000,是初始消耗的1/10左右。
注意:也可以使用PCA对特征降维,存储空间也可以节省很多。 -
为推荐系统提供支持。








 本文探讨了特征值、特征向量的概念及其在PCA和SVD中的应用,讲解了矩阵乘法背后的旋转与拉伸原理,以及如何通过SVD进行特征降维,节省存储空间,并应用于推荐系统。
本文探讨了特征值、特征向量的概念及其在PCA和SVD中的应用,讲解了矩阵乘法背后的旋转与拉伸原理,以及如何通过SVD进行特征降维,节省存储空间,并应用于推荐系统。
















 2536
2536

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








