文本相似性计算之编辑距离详解

最新推荐文章于 2025-02-24 09:00:00 发布

wenjieh_chen

最新推荐文章于 2025-02-24 09:00:00 发布

阅读量8.1k

点赞数 5

分类专栏：逝去的研究~ 文章标签：算法 python 字符串

本文链接：https://blog.csdn.net/wenjieh_chen/article/details/116157328

版权

逝去的研究~ 专栏收录该内容

2 篇文章

订阅专栏

文本相似性计算之编辑距离详解

概述:

编辑距离(Edit Distance)：是一个度量两个字符序列之间差异的字符串度量标准，两个单词之间的编辑距离是将一个单词转换为另一个单词所需的单字符编辑（插入、删除或替换）的最小数量。一般来说，编辑距离越小，两个串的相似度越大。
编辑距离是1965年由苏联数学家Vladimir Levenshtein发明的。Levenshtein Distance也被称为编辑距离（Edit Distance）。

一、Levenshtein.distance(str1, str2);

计算编辑距离(也称Levenshtein距离) 。算法实现:动态规划
定义：
对于两个字符串a、b，长度分别为|a|、|b|，它们的Levenshtein Distance为：
在这里插入图片描述

i和j分别表示字符串a和字符串b的下标。下标从1开始。
例如将kitten-字转成sitting: (kitten’和’sitting’的编辑距离为3) .
在这里插入图片描述

相似度=1-编辑距离/Math.Max(str1.length,str2.length)=1-3/7=0.571

运算过程：

建立一个矩阵，用来存储上一步计算好的距离

建立一个矩阵，用来存储上一步计算好的距离

matrix_ed=np.zeros((len(str_a)+1,len(str_b)+1),dtype=np.int)

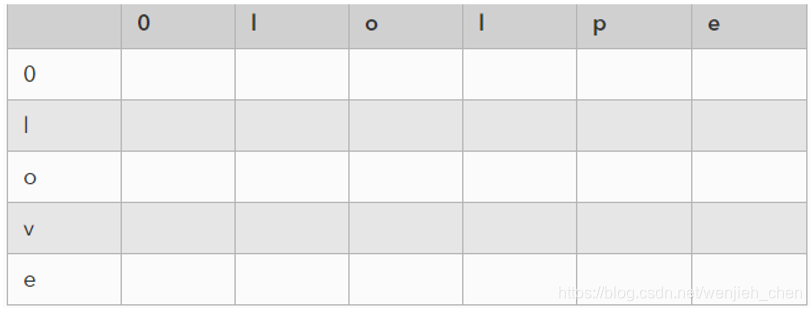
在这里插入图片描述

初始化第一行和第一列所有的距离。即：

matrix_ed[0]=np.arange(len(str_b)+1)
matrix_ed[:,0] = np.arange(len(str_a) + 1)

在这里插入图片描述

开始循环计算所有的距离,直到最后一个字符。例如:

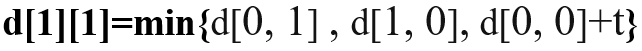
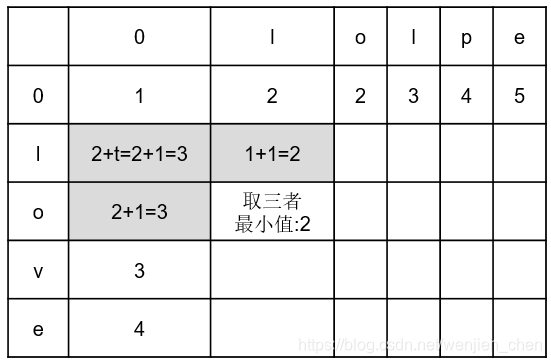
最后可以得到：
在这里插入图片描述
扫描完后，返回矩阵的最后一个值d[n][m]即是它们的距离。
所以，我们得到字符串a和b的编辑距离为2.

def lev(str_a,str_b):
    """
    ED距离，用来衡量单词之间的相似度
    :param str_a:
    :param str_b:
    :return:
    """
    str_a=str_a.lower()
    str_b=str_b.lower()
    matrix_ed=np.zeros((len(str_a)+1,len(str_b)+1),dtype=np.int)
    matrix_ed[0]=np.arange(len(str_b)+1)
    matrix_ed[:,0] = np.arange(len(str_a) + 1)
    for i in range(1,len(str_a)+1):
        for j in range(1,len(str_b)+1):
            # 表示删除a_i
            dist_1 = matrix_ed[i - 1, j] + 1
            # 表示插入b_i
            dist_2 = matrix_ed[i, j - 1] + 1
            # 表示替换b_i
            dist_3 = matrix_ed[i - 1, j - 1] + (1 if str_a[i - 1] != str_b[j - 1] else 0)
            #取最小距离
            matrix_ed[i,j]=np.min([dist_1, dist_2, dist_3])
    print(matrix_ed)
    return matrix_ed[-1,-1]

思考：
假设字符串a=‘love’,b=‘sffg’,c=‘lovefghaa’ 那么如果我们用上面计算出a和b,c的距离：
lev(a,b)=4,lev(a,c)=5

看到a和b的距离比a和c的距离要小，这种是不合理的。那么我们可以讲字符串替换的距离变大一点，改成2.
在这里插入图片描述

这样，就可以比较有效区分这种情况

二、Levenshtein.hamming(str1, str2)；

计算汉明距离。要求str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数。

三、Levenshtein.ratio(str1, str2)；

计算莱文斯坦比：
r= (sum-ldist) / sum
其中sum是指str1和str2字串的长度总和，l_dist是类编辑距离。注意这里是类编辑距离,在类编辑距离中删除、插入依然+1,但是替换+2.

四、Levenshtein.jaro(s1, s2)；

计算jaro距离(又称Jaro similarity), 这是由Matthew A. Jaro在1989年提出的算法. Jaro Distance据说是用来判定健康记录上两个名字是否相同,也有说是用于人口普查。完全不同的字符串为0，相同的字符串为1。我们先来看一下Jaro Distance的定义。
两个给定字符串s_1和s_2的Jaro Distance为:
在这里插入图片描述
其中〖|s〗_i |是字符串s_i的长度;m为s_1、s_2匹配的字符数量；t是字符转换的次数；
两个分别来自s_1与s_2的字符如果相距不超过匹配窗口
m_w=⌊max⁡〖(|s_1 |,|s_2 |)〗/2⌋-1
(下文解释)时,我们就认为这两个字符是匹配的(具体例子见下节匹配窗口m_w);
而这些相互匹配的字符则决定了换位的数目t。简单来说将s_1与s_2匹配的字符进行比较，相同位置但字符不同的字符数除以2就是要转换的次数t。
举例来说, MARTHA与MARHTA的字符都是匹配的,所以m=6；但是这些匹配的字符中,T和H要换位才能把MARTHA变为MARHTA,那么T和H就是不同的顺序的匹配字符, t=2/2=1；
两个字符串的Jaro Distance即为:
在这里插入图片描述
匹配窗口m_w
上面提到了字符匹配的问题,那么什么情况下才是匹配的呢?这里就需要提到匹配窗口(matching window)的概念了。
Jaro算法的字符之间的比较是限定在一个范围内的,如果在这个范围内两个字符相等,那么表示匹配成功,如果超出了这个范围,表示匹配失败。而这个范围就是匹配窗口m_w,在Jaro算法中,它被定义为不超过(小于等于)下面表达式的值:

在这里插入图片描述
比如说字符串A(“bacde”)和B(“abed”),它的匹配窗口大小

在匹配的过程中,字符"a’、‘b’、d都是匹配的, indexinA(‘d’)=3, indexinB(‘d’)=3,二者的距离是0,小于匹配窗口大小。但对于e’,虽然两字符串都有e’这个字符,但它们却是不匹配的,因为’e的下标分别为4和2,距离为2 >m_w,所以e’是不匹配的。
在这个例子中,由于有3个字符匹配,因此m=3,换位数目表示不同顺序的匹配字符的个数。同样看这个例子, 'a和’b’都是匹配的,但’a’和’b’在两个字符串的表示为"ba…’’ .和"ab…"它们的顺序不同，因此这里换位数目transpositions =2,而t = transpositions /2 =1。
对于匹配窗口的含义,笔者的理解是:匹配窗口是一个阈值,在这个國值之内两个字符相等,可以认为是匹配的;超过了这个阈值,即使存在另一个字符与该字符相等,但由于它们的距离太远了,二者的相关性太低了,不能认为它们是匹配的。
从上面的公式可以看出,该算法强调的是局部相似度。对于任意字符串s_1和s_2,能求出它们长度〖|s〗_i |,，m和t,这样便能代入公式求得二者的相似度(Jaro similarity)。
从刚才的例子A(“bacde”)和B(“abed”)中, |s_1 |=5,|s_2 |=4, m=3, t=1,代入公式可得:
在这里插入图片描述
python 运行

安装lib

pip install jaro_winkler

程序运行

print(jaro.jaro_metric("MARTHA".decode("utf-8"),"MARHTA".decode("utf-8")))

五、Levenshtein.jaro_winkler(s1, s2)；

是一个度量两个字符序列之间的编辑距离的字符串度量标准，是由William E. Winkler在1990年提出的Jaro Distance度量标准的一种变体。
计算Jaro-Winkler距离,而Jaro-Winkler则给予了起始部分就相同的字符串更多的权重, 因为拼写错误更可能发生在单词结尾附近。他定义了一个前缀𝒫,给予两个字符串。如果前缀部分有长度为𝓁的部分相同，则jaro_winkler Distance为：
在这里插入图片描述
d_j是两个字符串s_1与s_2的jaro Distance;
𝓁是前缀的相同的长度,但是规定最大为4;
𝒫则是调整分数的常数,规定不能超过0.25,不然可能出现相似度d_w大于1的情况, Winkler将这个常数值设为0.1;
这样,上面提及的MARTHA和MARHTA的Jaro-Winkler Distance为:
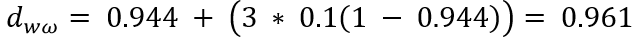
在这里插入图片描述
Jaro-Winkler Distance通过前缀因子𝒫使Jaro Distance相同时共同前缀长度𝓁越大的相似度越高。
图解Jaro-Winkler similarity求解过程

下面以字符串s_1(“abcdefgh”)和字符串s_2(“abehc”)为例来介绍整个算法的流程。这里以短字符串为行元素，长字符串为列元素，建立(|s_1|+1)×(|s_1|+1)的矩阵，这里匹配窗口的大小
在这里插入图片描述

(注意包括距离为0的匹配)，然后根据公式不断运算：
在匹配的过程中,字符"a’、‘b’、“c’、‘e’都是匹配的,所以m =4
如：indexins_1(‘a’)=0, indexins_1(‘a’)=0,二者的距离是0,小于匹配窗口大小。故字符’a’是匹配的;
indexins_1(‘b’)=1, indexins_1(‘b’)=1,二者的距离是0,小于匹配窗口大小。故字符’b’是匹配的;
indexins_1(‘c’)=2, indexins_1(‘c’)=4,二者的距离是2,小于匹配窗口大小。故字符’c’是匹配的;
indexins_1(‘e’)=4, indexins_1(‘e’)=2,二者的距离是2,小于匹配窗口大小。故字符’b’是匹配的;
indexins_1(‘h’)=7, indexins_1(‘h’)=3,二者的距离是4,大于匹配窗口大小。故字符’h’不匹配的;
m = 4，t = transportation/2=2/2 =1（"c’、‘e’位置不一致，需要转换，transportation=2）
故字符’f’、’g’、’d’不匹配;
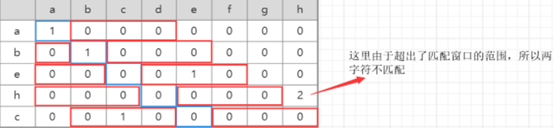
在这里插入图片描述

从上面的图以及公式,我们可以总结出求解的过程:字符串s1作为行元素,字符串s2作为列元素,窗口大小为m_w,同时建立两个布尔型数组,大小分别为s1和s2的长度,布尔型数组对应下标的值True表示已匹配, false表示不匹配。
对于行元素的每一个字符c1,根据c1在该字符串s1中的下标k,定位到s2的k位置,然后在该位置往前遍历m_w个单位,往后遍历m_w个单位,如果寻找到相等的字符,记在s2中的下标为p。经过这样的一次遍历,找到了k和p,我们分别标记布尔型数组s1的k和布尔型数组s2的p为已匹配(true),下次遍历时就跳过该已匹配的字符。当对s1的所有元素都遍历完毕时,就找到了所有已匹配的字符,我们统计已匹配的字符便能得到m。
然后对两个布尔型数组同时按照顺序比较,如果出现了true,但二者对应字符串相应位置的字符不相等,表示这是非顺序的匹配,这样就可以得到。这样就能根据m和求出Jaro similarity了。
至于Jaro-Winkler similarity,需要p参数,也不难,求出俩字符串最大共同前缀的大小即可。
如果读者对上面的过程还有疑问,笔者再提一点,关键就在于判断来自俩字符串的相等字符的距离是不是超过了阈值(即匹配窗口长度),这里的判断方法是在某个位置进行前后的搜索,包括当前位置。
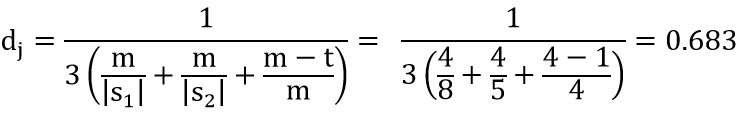
在这里插入图片描述
其中，字符串s_1(“abcdefgh”)和字符串s_2(“abehc”)共同前缀ab的长度𝓁 =2 < 4

经过上面的学习，我们已经掌握了这个算法的原理以及实现方法，下面我们接着来探究它的特性以及适用场景。
我们来看下面的一组实验结果
在这里插入图片描述
关键字是fox，另外的字符串是包含有fox几个字符的字符串，可以看出最高相似度的是"fox"在开始几位的情况下，而"afoxbcd"反而比"foaxbcd"更低，虽然前者含有完整的"fox"而后者是分开的。同时"abcdfox"的相似度为0，即使它末尾含有"fox”。
上面这几个例子说明了jaro-winkler相似度对于前缀匹配更友好，并且越往前面匹配成功带来的权重更大。由此可以看出，该算法可以用在单词的匹配上，比如对于一个单词"appropriate"，找出数据库中与它最匹配的一个词语，可以是"appropriation"，也可以是"appropriately"等。但是，该算法不适用在句子匹配上，因为如果关键字在句子的后面部分，相似度会急剧下降，甚至为0。
个人觉得算法可以完善的点:

去除停用词(主要是标点符号的影响)
针对中文进行分析,按照词比较是不是要比按照字比较效果更好?

参考链接：
https://zhuanlan.zhihu.com/p/91667128
https://blog.csdn.net/sinat_25394043/article/details/108404210
https://www.jb51.net/article/98449.htm
https://en.wikipedia.org/wiki/Jaro%E2%80%93Winkler_distance
http://www.coli.uni-saarland.de/courses/LT1/2011/slides/Python-Levenshtein.html#Levenshtein-inverse