原博客地址:http://blog.csdn.net/xiaowei_cqu/article/details/27692123
在实际计算时,三种方法计算的金字塔组数noctaves,尺度空间坐标σ,以及每组金字塔内的层数S是一样的。同时,假设图像为640*480的标准图像。
金字塔层数:
其中o_min = 0,对于分辨率为640*480的图像N=5。
每组金字塔内图像数:
S=3,即在做极值检测时使用金子塔内中间3张图像。
对于LoG每组金字塔内有S+2张图像(S=-1,0,1,2,3),需要做S+1次高斯模糊操作(后一张图像由前一张做高斯模糊得到);而DoG每组金字塔有S+3张高斯图像,得到S+2张DoG图像。
尺度空间系数:
其中,S表示每组金字塔内图像层数,n为当前高斯层数,取0-4。DoG需要5个尺度系数得到6张GSS图像,而LoG只需要前4个尺度系数得到5张图像。
LoG
高斯核使用正太分布(高斯函数)计算模糊模版,N维空间正太分布方程为:
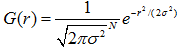
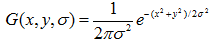
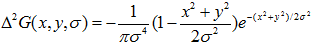
其中o为当前金字塔层数,n为在当前金字塔层中图像张数。
由于卷积计算性质:
在计算时,通过对前一张图像做尺度系数为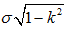

DoG
即,
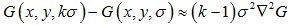
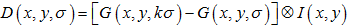
图 2. 由高斯金字塔得到DoG金字塔及其对应的尺度空间系数示意图。
LoG & DoG
一个直观的比较结果,使用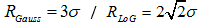
可以看到,LoG比DoG明显需要更多的加法运算和乘法运算。虽然DoG需要在每层金字塔多做一次高斯操作(即为了得到S+2张DoG图需要S+3张高斯模糊图),但通过减法取代LoG核的计算过程,显著减少了运算次数,大大节省了运算时间。








 本文详细介绍了LoG(拉普拉斯高斯)和DoG(高斯差分)两种算法在图像处理中的应用原理及实现过程。针对640*480分辨率图像,分析了金字塔组数、每组图像数以及尺度空间系数等参数设置,并对比了两种算法的计算复杂度。
本文详细介绍了LoG(拉普拉斯高斯)和DoG(高斯差分)两种算法在图像处理中的应用原理及实现过程。针对640*480分辨率图像,分析了金字塔组数、每组图像数以及尺度空间系数等参数设置,并对比了两种算法的计算复杂度。
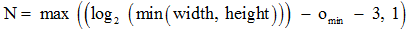
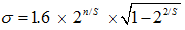
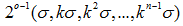

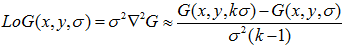


















 8146
8146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








