线性规划问题（LP问题）

线性规划问题

基本特征（什么是LP问题）

$$\begin{array}{ll}\mathrm{minimize}& c^{T}x+d\\ \text{ subject to }& Gx⪯h\\ & Ax=b\end{array}$$
一言以蔽之，目标函数和约束条件都是仿射函数。

几何意义（物理意义理解）

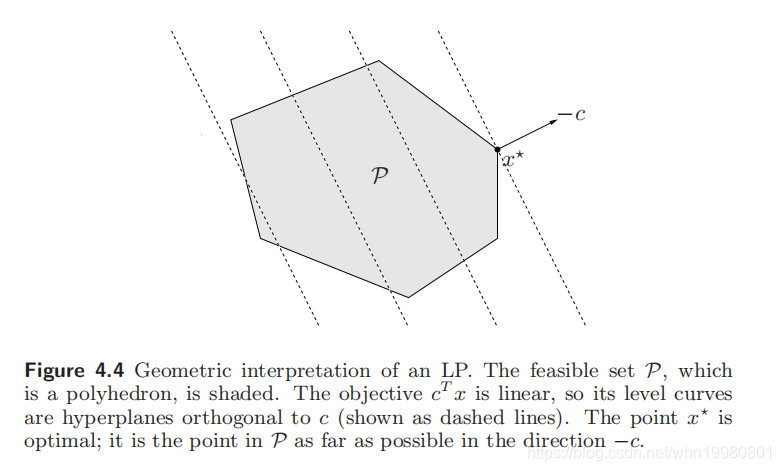
在多面体上，沿$-c$为法线方向，找到多面体$\mathcal{P}$的支撑超平面。

两种特殊形式（LP问题中被研究较透彻的两个方向）

标准形式的LP问题

不等式约束只有非负约束
$$\begin{array}{ll}\mathrm{minimize}& c^{T}x\\ \text{ subject to }& Ax=b\\ & x⪰0\end{array}$$

一般LP问题如何转化为标准LP问题

第一步：引入松弛变量$s$，变不等式约束为等式约束
$$\begin{array}{ll}\mathrm{minimize}& c^{T}x+d\\ \text{ subject to }& Gx+s=h\\ & Ax=b\\ & s⪰0\end{array}$$
然而标准形式中的不等式约束是对优化变量来说的，如果到此为止，则只是对松弛变量。所以
第二步：用两个有非负约束的优化变量$x=x^{+}-x^{-}$替代原优化变量$x$，则原优化问题变为：
$$\begin{array}{ll}\mathrm{minimize}& c^T{x}^{+}-c^T{x}^{-}+d\\ \text{ subject to }& G{x}^{+}-G{x}^{-}+s=h\\ & A{x}^{+}-A{x}^{-}=b\\ & x^{+}⪰0,x^{-}⪰0,s⪰0\end{array}$$
最后写成标准形式：
$$\begin{array}{rl}& \min \left[\begin{array}{lll}{\mathbf{c}}^T& -{\mathbf{c}}^T& 0^T\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{+}\\ {\mathbf{x}}_{\mathbf{s}}\end{array}\right]\\ & \text{ s.t. }\left[\begin{array}{c}{\mathrm{x}}_{+}\\ {\mathrm{x}}_{-}\\ \mathrm{s}\end{array}\right]⪰0,\left[\begin{array}{lll}\mathrm{G}& -\mathrm{G}& \mathbf{I}\end{array}\right]\left[\begin{array}{c}{\mathrm{x}}_{+}\\ {\mathrm{x}}_{-}\\ \mathrm{s}\end{array}\right]=\mathrm{h}\end{array}$$

不等式形式的LP问题

即没有等式约束
$$\begin{array}{ll}\mathrm{minimize}& c^{T}x\\ \text{ subject to }& Ax⪯b\end{array}$$

例子

多面体的Chebyshev中心

在多面体中寻找最大的欧式球，多面体表述：
$$\mathcal{P}=\left\{x\in {\mathbf{R}}^n\mid a_i^{T}x\le b_i,i=1,\dots ,m\right\}$$
欧式球表述：
B = { x c + u ∣ ∥ u ∥ 2 ≤ r } \mathcal{B}=\left\{x_{c}+u \mid\|u\|_{2} \leq r\right\} B={xc​+u∣∥u∥2​≤r}
其中$x_c$为球心，则欧式球在多面体中表述为：
$$a_i^T\left(x_c+u\right)\le b_i$$
其中左式可以继续展开得到欧式球中满足不等式约束的上限：
$$\begin{array}{rl}{a}_i^T\left(x_c+u\right)& =a_i^T{x}_c+a_i^{T}u\\ & \le a_i^T{x}_c+||a_i|{|}_2||u|{|}_2\\ & \le a_i^T{x}_c+||a_i|{|}_{2}r\end{array}$$
所以优化问题为：
$$\begin{array}{rl}& \text{ maximize }r\\ & \text{ subject to }{a}_i^T{x}_c+r{\Vert a_i\Vert }_2\le b_i,i=1,\dots ,m\end{array}$$

分片线性最小化

对于无约束分片线性凸函数问题：
$$f(x)=\underset{i=1,\dots ,m}{\max }\left(a_i^{T}x+b_i\right)$$
可以转化为LP问题。
首先改写为上境图形式：
$$\begin{array}{rl}& \text{ minimize }t\\ & \text{ subject to }\underset{i=1,\dots ,m}{\max }\left(a_i^{T}x+b_i\right)\le t\end{array}$$
再将约束条件拆开为多个不等式约束
$$\begin{array}{rl}& \text{ minimize }t\\ & \text{ subject to }\left(a_i^{T}x+b_i\right)\le t\end{array}$$

线性分式规划

$$\begin{array}{ll}\mathrm{minimize}& f_0(x)=\frac{c^{T}x+d}{e^{T}x+f}\\ \text{ subject to }& Gx⪯h\\ & Ax=b\end{array}$$
定义域为：$\mathrm{dom}{f}_0=\left\{x\mid e^{T}x+f>0\right\}$
该问题为拟线性问题，可以转化为LP问题：
$$\begin{array}{ll}\mathrm{minimize}& c^{T}y+dz\\ \text{ subject to }& Gy-hz⪯0\\ & Ay-bz=0\\ & e^{T}y+fz=1\\ & z\ge 0\end{array}$$
优化变量为$y$和$z$。
当原问题有最优解$x$，LP问题最优解为：
$$y=\frac{x}{e^{T}x+f},z=\frac{1}{e^{T}x+f}$$
当LP最优解为$\left(y,z\right)$，则有两种情况：
1.如果$z\ne 0$，$x=\frac{y}{z}$
2.如果$z=0$，且有一个最优点$x_0$，则最优解可表示为$\text{for all }t>0,x=x_0+ty$，此时LP问题的解是线性分式规划最优解的上确界。

广义线性分式规划

$$f_0(x)=\underset{i=1,\dots ,r}{\max }\frac{c_i^{T}x+d_i}{e_i^{T}x+f_i},\mathrm{dom}{f}_0=\left\{x\mid e_i^{T}x+f_i>0,i=1,\dots ,r\right\}$$