http://blog.csdn.net/yuzhongchun/article/details/40433405
说明:这是一篇来自土耳其中东技术大学的2010年的硕士论文,主要讲述了在推荐系统中应用SVD方法。
这篇文章可以到http://download.csdn.net/detail/yuzhongchun/8078769下载。
Abstract
本文提出两个创新点:第一个是先将user与item分类,然后根据分类将矩阵分成相应的“子矩阵”,对这些矩阵进行相应的SVD,实验表明这样做不仅会提高准确率还会降低计算复杂度;另一个是向<user, item>二维矩阵中引入tag,使其成为<user, item, tag>三维矩阵,再通过矩阵分解成<user, item>、<user, tag>、<item, tag>子矩阵,最后再进行SVD,实验表明引入tag会提高推荐性能。
Chapter 1 Introduction
随着用户和物品规模的迅速增长,推荐系统面临两个主要挑战:第一个是提高推荐质量,第二个是提升推荐算法的可扩展性。这两个挑战是有冲突的。
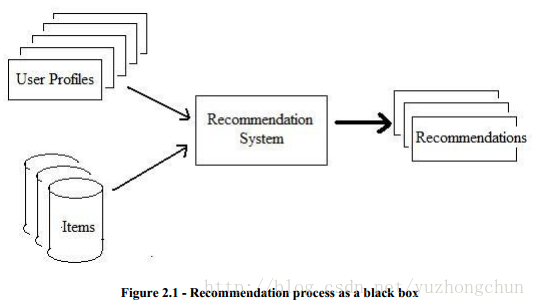
一个推荐系统由三部分组成:background data,它是推荐处理开始之前的系统信息;input data,它是用于必须与系统交互的信息;an algorithm,它是把background data和input data结合起来生成推荐的算法。
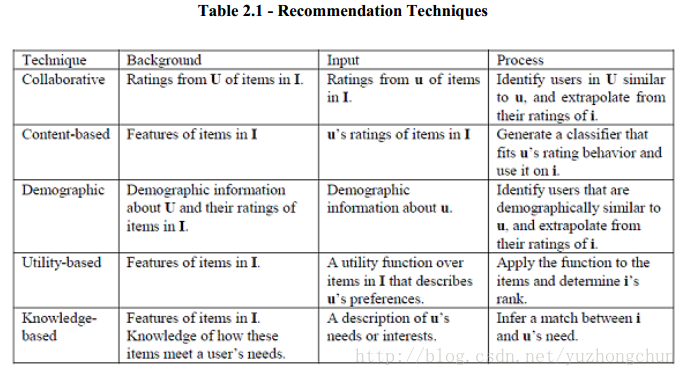
推荐技术可以分为五种:collaborative, content-base,demographic, utility-based, and knowledge-based。一些混合的算法是由这五种技术组合而成的。协同推荐(collaborativerecommendation)是最常见,实现最广的一种。
SVD提供原始矩阵的低秩线性近似(low-rank linearapproximation),而且低秩线性近似比原始矩阵更好。研究者们指出在大多数时候,基于SVD的方法产生的推荐结果比传统的协同过滤算法更好。但是,SVD需要更复杂的矩阵计算,这使得基于SVD的推荐系统不适合于大规模的系统。
本文,提出了两点:一是Users和Items的分类,实验表明item和user分类不仅能提高推荐质量,而且能提升SVD技术的性能;二是引入tags到传统的二维SVD方法,实验表明tags也可以提升性能。
chapter2 详细论述了推荐系统和推荐处理过程。
chapter3 举例讲述了SVD方法。
chapter4 讲述了现有的SVD推荐方法,并且提出了自己的方法。
chapter5 进行了实验,比较现有方法与本文所提出的方法。
chapter6 结论,并指出未来的研究点。
Chapter 2 Recommender Systems
2.1 Definition of a Recommender-System (RS)
推荐系统包括两个基本部分:用户的偏爱信息,决定一个用户是否对一个物品感兴趣的方法
2.1.1 Recommendation Process
推荐处理过程如下图:
2.2 Recommendation Techniques
推荐技术可以分为如下图所示的5种:
2.2.1 CollaborativeRecommendation
可以分为基于内存的算法(Memory-basedAlgorithms)和基于模型的算法(Model-basedAlgorithms)。
2.2.1.1 Memory-basedAlgorithms
主要的基于内存的方法有:
Ø User-basedApproaches
基于用户的推荐算法
Ø Item-basedApproaches
基于物品的推荐算法
这两种方法是协同过滤算法中的常见算法,关键在于相似度的计算。
2.2.1.2 Model-basedAlgorithms
基于模型的算法使用评分集合作为训练集来学习一个模型,用这个模型去预测评分。基于模型的方法往往要花费比较多的时间去构建和更新模型。基于模型的推荐常用很多的学习技术包括神经网络,隐语义索引和贝叶斯网络。
2.2.2 Content-based Recommendation
基于内容的推荐时信息过滤研究的结果和继续。
2.2.3 Demographic Recommendation
基于统计的推荐旨在根据个人属性对用户进行分类,然后根据统计分类进行推荐。基于统计的推荐的优点在于它不需要用户评分的历史数据,而这些信息是协同过滤和基于内容的推荐所必须的。
2.2.4 Utility-base Recommendation
基于效用的推荐根据每个物品的效用的计算为用户做推荐,关键性的问题是怎么去为每个用户创建一个效用函数。基于效用的推荐优点是它可以把非物品属性,比如卖家的可靠性和产品的实用性,分解成效用计算。
2.2.5 Knowledge-basedRecommendation
基于知识的推荐试图根据用户的需要和偏爱的推理来推荐。基于知识的推荐有两个功能知识:
Ø 一个物品怎样满足一个用户的需求;
Ø 给出一个可能的推荐能够满足一个需求的原因。
2.3 Hybrid Recommendation Systems
混合推荐系统
RobinBurke的”Hybrid Recommender System: Survey andExperiments”(2002)是一篇有关不同混合推荐算法设计方案的著名调研报告。它给出了各种推荐算法的分类标准。本文即是参考这篇文章讲述的混合推荐。
Ø Weighted: 加权式混合,通过计算两个或多个推荐系统结果分数的加权和,将它们组合在一起。
Ø Switching: 切换式混合,需要一个权威者根据用户记录或推荐结果的质量来决定在哪种情况下采用哪种推荐系统。
Ø Mixed: 交叉式混合,在用户交互界面这个层面上将不同推荐系统的结果组合在一起,各种方法所得到的结果被一起呈现。
Ø Feature Combination: 特征组合的混合方案,使用不同推荐技术的特征进行推荐。
Ø Cascade: 串联混合,将一组推荐方法按顺序排列,后面的推荐方法对前面的推荐结果做优化。
Ø Feature Augmentation: 特征补充的混合方案
Ø Meta-level: 分级混合,一种推荐方法构建的模型被主推荐方法用来生成推荐结果。
总结:
第二章节主要介绍了推荐系统的基本知识,包括什么是推荐系统,推荐系统的处理流程和推荐系统的常用技术;重点介绍了推荐系统的常用技术。
下表是根据论文内容和其它资料整理的的一个大致的分类:
| 协同过滤推荐 | 基于内存的推荐 | 基于用户的最近邻推荐 |
| 基于物品的最近邻推荐 | ||
| 基于模型的推荐 | 矩阵分解、LSA、pLSA、LSI、PCA(主成分分析)、LFA(Latent Factor Model)、LDA、Topic Model | |
| 基于内容的推荐 | ||
| 基于知识的推荐 | ||
| 混合推荐 | 整体式混合设计 | 特征组合的混合方案 |
| 特征补充的混合方案 | ||
| 并行式混合设计 | 交叉式混合 | |
| 加权式混合 | ||
| 切换式混合 | ||
| 流水线混合设计 | 串联混合 | |
| 分级混合 | ||
下表来自《程序员》杂志2013精华版:
|
| 基于内存(启发式算法) | 基于模型 |
| 基于内容 | TF-IDF 聚类 最大熵 相似性度量 | 贝叶斯分类器 决策树 神经网络 专家系统 知识推理 |
| 协同过滤 | K近邻 聚类 链接分析 关联规则 相似性度量 | 贝叶斯分类 决策树 神经网络 矩阵分解 概率模型 图模型 Boosting Topic Model 回归分析 |
| 混合式 | 线性组合 投票机制 meta-heuristics | Ensemble 统一推荐框架 |
Chapter 3 Singular Value Decomposition
第3章节,作者用实例讲述了什么是SVD,怎么进行SVD。更详细的说明可以参考KirkBaker的”Singular Value Decomposition”, 2005。
3.1 Singular Value Decomposition (SVD)
3.1.1 Definition of SVD
SVD可以看作是数据简化(数据融合)的一种方法。SVD是一种矩阵分解技术。
奇异值分解可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要特性。
SVD实际上是数学专业内容,但它现在已经渗入到不同的领域中。比如,Netflix(一个提供在线电影租赁的公司)曾经就悬赏100万美金,如果谁能提高它的电影推荐系统评分预测准确率提高10%的话。令人惊讶的是,这个目标充满了挑战,来自世界各地的团队运用了各种不同的技术。最终的获胜队伍"BellKor's PragmaticChaos"采用的核心算法就是基于SVD。SVD提供了一种非常便捷的矩阵分解方式,能够发现数据中十分有意思的潜在模式。
3.1.2 Example of SVD
使用一个具体的例子,讲述怎么进行SVD。这里不再列出,有兴趣的可以参看论文,以及Kirk Baker的”Singular ValueDecomposition”, 2005。
有两篇讲述SVD很好的博客,可以参看下:
1) 矩阵奇异值分解及其应用
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
2) 奇异值分解及几何意义
http://blog.csdn.net/redline2005/article/details/24100293
Chapter 4 Recommendation With SVD
4.1 Recommendation Using SVD
基于协同过滤的推荐算法面临诸如稀疏性、可扩展性和同义性(synonymy)等问题。为了去除一个大的又稀疏的数据集的噪声数据,提出了一些降维的方法。LSI(Latent SemanticIndexing, 隐语义索引)是一种广泛用于用户-物品评分矩阵降维的技术,能很好的应对协同过滤算法的挑战。基于SVD的推荐算法有很高的推荐质量,但计算比较复杂。
4.1.1 Dimensionality Reduction
SVD能提供原始矩阵的最好的低阶线性近似。通过选取最大的k个奇异值可以降低原始矩阵的纬度。k的值可能会根据数据的大小和结构而变化(《机器学习实战》一书第14章利用SVD简化数据中讲到一个典型的做法是保留矩阵中90%的能量信息,即将奇异值的平方和累加到总值的90为止)。
假设数据矩阵Data,纬度为m*n,即有m个用户,n个物品,SVD分解可以用下面的公示表示:
上面的公式中,Σ只有对角元素,其余元素都为0,此外,Σ的对角元素都是按照从大到小排列的,这些对角元素成为奇异值。
4.1.2 SVD Recommendation Algorithms
4.1.2.1 User-based Similarity
在推荐系统算法中一步关键的算法是计算用户之间的相似度,一般采用余弦相似度或欧氏距离。
基于用户相似度的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 从原始矩阵A中找出对Item=y评过分的所有用户;
2) 使用降维矩阵,找出对Item=y评过分的与User=x最相近的那个User;
3) 从原始矩阵中获取最相似用户对Item=y的评分,并把这个评分当做User=x对Item=y的评分。
在第二步中,如果User=x已经在降维矩阵中,则按上面步骤计算;如果User=x是一个新的用户,在计算相似度之前,这个新用户必须冲n维空间投影到k维空间中。
如果知道SVD的空间几何意义,理解投影过程就很简单:原来的用户的评分向量Nu(1xn)是在V空间中(n维),将其与Vk矩阵相乘就知道这个用户向量的坐标,然后根据S进行坐标缩放(同时截取前k个值即可),获得的坐标就是用户的评分向量Nu在U空间中的坐标了。
用数学表达的话,设用户向量是Nu,投影到U空间后的向量为P,则有:
然后就可以计算这个用户(用P向量)与其他用户(Uk的各行向量)之间的相似度了。
大量的实验表明,计算相似度的话还是使用欧式距离比较有效。上面的算法瓶颈是如何在“茫茫人海”中找到最相似的那个User。
4.1.2.2 Item-based Similarity
使用基于物品的推荐不存在上面的计算瓶颈,因为我们探索的是物品之间的相似度而不是用户之间的相似度。在大多数系统中,物品比用户更稳定,不经常变化。所以,基于物品的相似度非常适合预计算。
相类似的,如果要计算两Item之间的相似度需要使用Vk矩阵。Vk 每一行代表一个Item,行之间越相近则代表Item之间越相似。其计算过程与上面所讲的User之间的推荐过程很接近。
基于物品相似度的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 从原始矩阵A中找到被User=x评过分的那些items;
2) 使用降维矩阵,找出被User=x评过分的跟Item=y最相似的那个Item;
3) 从原始矩阵A中获取被User=x评过分的最相似的Item的评分,并把这个评分当做User=x对Item=y的评分。
与基于用户相似度推荐类似,在第二步计算中,如果Item=y已经在降维矩阵中,则可计算;如果Item=y是一个新物品,则要先做投影,然后再计算。
设新的Item评分向量是Ni(mx1),处于U空间(m维),需要投影到Vk空间(n维)。首先通过内积计算Ni在U空间中的坐标,然后使用Sk反向伸缩坐标即可得到在V空间的坐标。
用数学表达的话,设用户向量是Ni,投影到V空间后的向量为P,则有:
4.2 Incremental SVD
在一个推荐系统中,整个算法是分两步的。第一步是离线训练,第二步是在线执行。上面所讲述的用户相似度和物品相似度的计算都属于离线计算。一般的离线SVD对于m*n的矩阵,计算复杂度为,非常的费时。
一个解决的方法是使用“folding-in”,进行增量SVD,如下图所示:
增量SVD的一个好处是不会影响之前存的的User或Item的坐标,当用户添加到已经分解的SVD模型中,所付出的时间复杂度仅为O(1)。
每次离线计算时再全部重新SVD,而线上运行时只进行增量SVD。
4.3 Contributions to SVD-based Recommendation
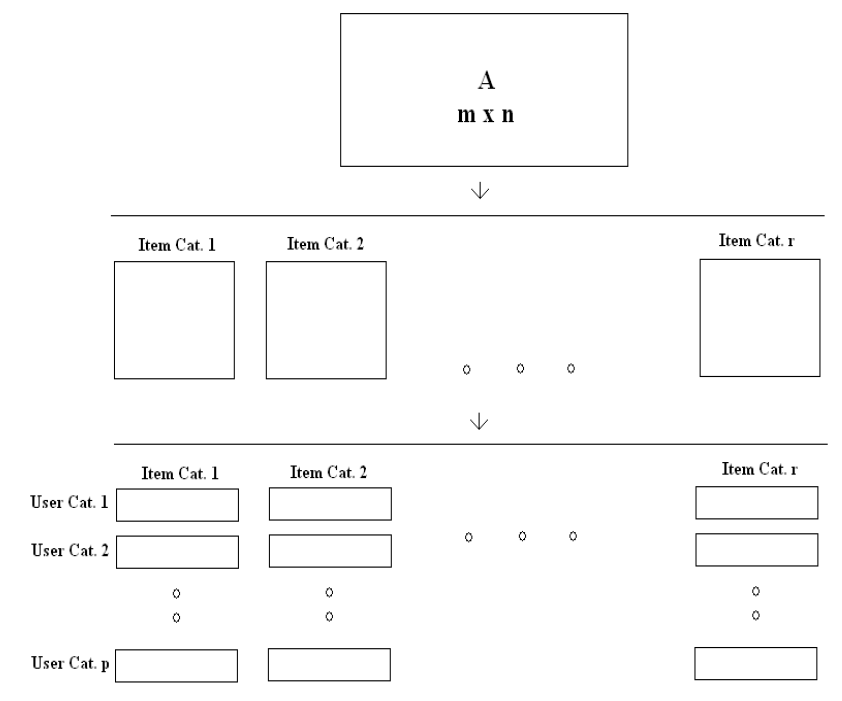
4.3.1 Categorization of Users and Items
分类之后再逐个SVD,可以明显减少时间。
从原始矩阵我们可以得到r*p个矩阵。对这些矩阵,分别进行SVD。
基于分类数据(用户相似度)的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 找出User=x的用户分类;
2) 找出Item=y的物品分类;
3) 这出这些分类对应的矩阵;
4) 在这个用户分类中找出对Item=y评过分的所有用户;
5) 在这个矩阵上进行SVD,找出与User=x最相似的用户;
6) 把最相似用户对Item=y的评分给Rating。
基于分类数据(物品相似度)的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Raging=?
1) 找出User=x的用户分类;
2) 找出Item=y的物品分类;
3) 这出这些分类对应的矩阵;
4) 在这个物品分类中找出被User=x评过分的所有物品;
5) 在这个矩阵上进行SVD,找出与Item=y最相似的物品;
6) 把最相似物品的评分给Rating。
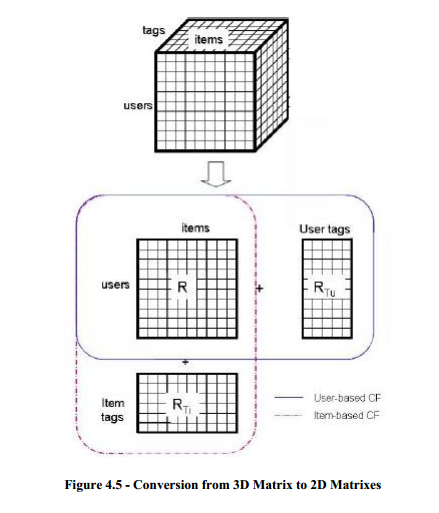
4.3.2 Adopting Tags to SVD Recommendation
为了提高推荐质量,一些元信息例如物品的内容信息已经被用作额外的知识。随着一些允许用户写物品标签的系统的流行,标签成为了一个对推荐算法很有用的信息。本文把标签引入到推荐算法中,为了使标签能适合一般的SVD算法,我们把三维矩阵<user, item, tag>降成三个二维矩阵<user, item>,<user, tag>,<item, tag>。
4.3.2.1 Extension with Tags
用户标签是用户u写的来标记物品的,可以被看成用户物品矩阵中的物品。物品标签是用户描述物品i的标签,扮演者用户物品矩阵中的用户角色。
另外,聚类方法也可以应用到标签中以使类似的标签聚类到一块。在本文中,作者使用子字符串,java字符串比较和编辑距离(edit distance)计算方法来聚类相类似的标签,以提高推荐的性能。
Edit Distance
在信息理论和计算机科学中,两个字符串的edit distance是一个字符串转换为另一个字符串所需要的操作数。有一些不同的方法来定义edit distance,相对应的有不同的算法去计算它的值。在本文中,作者使用”Levenshtein Distance”。
例如,”kitten”和”sitting”的Levenshtein Distance,如下所示:
1.kitten –> sitten (substitutionof ‘s’ for ‘k’)
2.sitten -> sittin (substitutionof ‘i’ for ‘e’)
3.sittin -> sitting (insert‘g’ at the end)











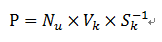
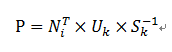















 38
38

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








