直接上题,不墨迹
设函数在区间
上连续,在
内可微,且
1,证明:存在一个
,使得
2,证明:存在一个
3,若
,A,B为正常数,证明:对任意
,有
第一题,常规,不多说
1,令
则
有零点定理可知,得证
第二题,说实话,不难,但思路真的很重要,有时候想错了,可能就走远了,一开始我就想错了。
这种题就是构造辅助函数,可能是最近手生疏了,少做题了一开始想构造的函数居然是有关积分上限的函数就像这样:,想到这种无非就是把题目中要求证的结果再积分回去,得到这样的例子,虽然这个题目不适用,但是几个月前,我碰到类似的证明题,就是要用到类似证法,要用到积分上限的型式。
但在这个题,我们明显的要用罗尔的构造型式: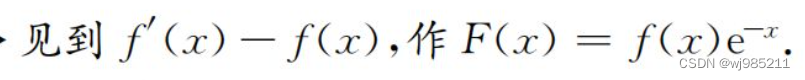
2,令
则
则
用罗尔定理.....
得证
第三题,才是重头戏,条件看起来毫无厘头,却让我们证明一堆绝对值,而且附带A,B
在看这题前我们得先想到泰勒公式,
其实在做这题前,我是一点都没有思路,最后也是在网上找到了思路,因为最近几年的专升本考试也是跟泰勒公式有关系,而且这题也有和泰勒有关,所以我在这么必须来一遍,本来想到是图片截一张,放上去的,想想还是算了,必须写一遍印象加固一下。
,其中
在x与x0之间
则
所以
所以
然后把该大绝对值都放到一个小函数值中,然后再根据
,f0和f1都为0
最后变能得出答案。
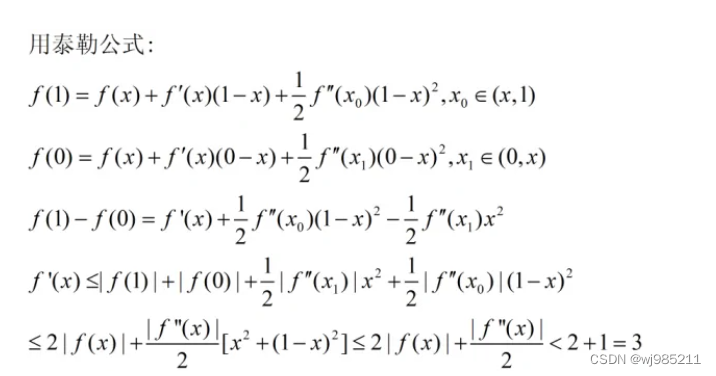 最后用网上的图来完善一下。
最后用网上的图来完善一下。























 8450
8450











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








