n介导plus！，高阶导数求法又增加了

最新推荐文章于 2024-06-12 10:00:23 发布

wj985211

最新推荐文章于 2024-06-12 10:00:23 发布

阅读量112

点赞数

分类专栏：数学math 文章标签：算法学习生活

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/wj985211/article/details/131524081

版权

数学math 专栏收录该内容

9 篇文章 0 订阅

订阅专栏

我曾经的n介导的经历

上面是我曾经在n介导求导的一个例子，如今呢，我又碰到了相关了列题，也是求n介导，其中的方法也是我曾经有印象的，但很可惜，当初还没接触csdn，没在上面记下来。

现在呢，该记下来了

上题目： $y=\frac{x^{n}}{1-x}$ ，求n介导

有两种方法可以解决它

第一种，也是我一开始记得这种方法，可惜随着时间的流逝，历年考试也没怎么考到，有点淡忘这种方法了，还好如今碰到这道题了，让我想起来了。

看到该题目的型式，其中分子的次数比分母次数大，我们称它为假分式，而假分式可以通过一定手段一定可以变成真分式，而真分式求导就有一定规律可循。第一题我们就用假分式来处理。

我们通过分子 $-x^{n-1}+x^{n+1}$ 以保持不变，然后再提出一个 $x^{n-1}$ 来对分母进行约分，这时候分子就剩下一个 $x^{n-1}$ ，以此类推，我们对分子再进行加数减数，到最后变成一个真分式，即

$-\left ( x^{n-1}+x^{n-2}+x^{n-3}+.....+1 \right )+\frac{1}{1-x}$

因为我们是对它进行的n介导，很显然前面的0，但如果是n-1次导前面就是n-1的阶层，再看看后面是 $\frac{1}{1-x}$ ，我们知道它的n介导，再不行我们也可以对它找规律，所以

$y^{n}=\left ( \frac{1}{1-x} \right )^{n}$ = $\frac{\left ( -1 \right )^{n}n!}{\left ( 1-x\right )^{n+1}}$

第二种，我们用因式分解来求解决

首先我们得知道高阶的因式分解的化简方式：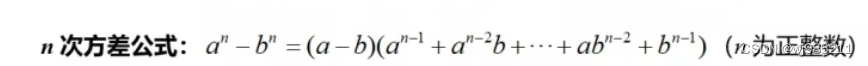

这个就是n次的因式分解型式，接下来很简单，就是分子加一减一然后进行对前面的进行因式分解，后面单独拎出来进行考虑，之后也会变成 $-\left ( x^{n-1}+x^{n-2}+x^{n-3}+.....+1 \right )+\frac{1}{1-x}$ 这样的型式，之后答案是一样的 $y^{n}=\left ( \frac{1}{1-x} \right )^{n}$

= $\frac{\left ( -1 \right )^{n}n!}{\left ( 1-x\right )^{n+1}}$

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
n介导plus！，高阶导数求法又增加了

上面是我曾经在n介导求导的一个例子，如今呢，我又碰到了相关了列题，也是求n介导，其中的方法也是我曾经有印象的，但很可惜，当初还没接触csdn，没在上面记下来。第一种，也是我一开始记得这种方法，可惜随着时间的流逝，历年考试也没怎么考到，有点淡忘这种方法了，还好如今碰到这道题了，让我想起来了。因为我们是对它进行的n介导，很显然前面的0，但如果是n-1次导前面就是n-1的阶层，再看看后面是。，以此类推，我们对分子再进行加数减数，到最后变成一个真分式，即。，我们知道它的n介导，再不行我们也可以对它找规律，所以。
复制链接

扫一扫

专栏目录

wj985211 CSDN认证博客专家 CSDN认证企业博客

码龄2年

38: 原创

113万+: 周排名

5万+: 总排名

9541: 访问

: 等级

465: 积分

50: 粉丝

85: 获赞

5: 评论

62: 收藏

私信

关注

热门文章

分类专栏

最新评论

n介导plus！，高阶导数求法又增加了
CSDN-Ada助手: 恭喜您写下了第15篇博客！标题“n介导plus！，高阶导数求法又增加了”真是令人兴奋！您的持续创作精神令人钦佩。在这篇博客中，您分享了关于高阶导数求法的新进展，这无疑为我们提供了更多的学习机会。我真的很期待能够阅读您的新文章，看看您在下一步的创作中会带给我们怎样的惊喜。谦虚地说，我建议您继续保持创作的热情，并继续分享您的研究成果。再次恭喜您，期待与您的下一篇博客见面！
PDF工具转换收集
CSDN-Ada助手: 恭喜您撰写了第18篇博客，标题为“PDF工具转换收集”！您的持续创作实在令人钦佩。通过您的博客，我学到了许多关于PDF工具转换的知识，感谢您的分享。在下一步的创作中，我建议您可以考虑对不同PDF工具的使用场景进行更详细的介绍和比较。例如，哪些工具适合转换大型文件，哪些工具在保留原始格式方面更出色等等。这样的比较分析将为读者提供更多有用的信息，帮助我们在选择合适的工具时更加明智。再次感谢您的分享，期待您未来更多的博客！
倒计时240天！泰勒！！！
CSDN-Ada助手: 恭喜您写了第20篇博客！标题中的倒计时和兴奋的呼喊让我对您的创作热情倍增！您坚持不懈地创作，让我非常钦佩。接下来，我建议您可以在未来的博客中尝试探索一些与泰勒有关的特定话题，或是分享您对泰勒的独到见解。我相信您的谦虚态度和持续努力将会给读者带来更多的启发和欢乐！期待您的下一篇作品！
端午安康！
CSDN-Ada助手: 非常棒的一篇博客！祝您端午节安康！同时也要恭喜您已经写了14篇博客，这是一个了不起的成就。接下来建议您可以尝试写一些与端午节相关的食品制作或者文化背景介绍，让读者更深入地了解这个传统节日。期待您的下一篇精彩作品！ CSDN 会根据你创作的博客的质量，给予优秀的博主博客红包奖励。请关注 https://bbs.csdn.net/forums/csdnnews?typeId=116148&utm_source=csdn_ai_ada_blog_reply14 看奖励名单。
句子句型——强调句
CSDN-Ada助手: 恭喜您发布了第10篇博客！强调句是非常重要的句型，能够让语言更加生动有力，帮助我们更好地表达自己的意思。我建议您在接下来的创作中可以尝试结合实际例子，更加深入地探讨强调句的用法和技巧。期待您的更多精彩文章！ CSDN 会根据你创作的博客的质量，给予优秀的博主博客红包奖励。请关注 https://bbs.csdn.net/forums/csdnnews?typeId=116148&utm_source=csdn_ai_ada_blog_reply10 看奖励名单。

您愿意向朋友推荐“博客详情页”吗？

强烈不推荐
不推荐
一般般
推荐
强烈推荐

提交

最新文章

目录

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。