工具系列：时间序列预测工具Dart介绍_时间序列预测的迁移学习

概述

本笔记本的目标是探索时间序列预测的迁移学习，即在一个时间序列数据集上训练预测模型，并在另一个数据集上使用它。该笔记本是100%自包含的，即它还包含安装依赖项和下载使用的数据集的必要命令。

根据什么构成“学习任务”，我们在这里所称的迁移学习也可以从元学习的角度来看（或称为“学习如何学习”），在推理时模型可以自适应新任务（例如预测新的时间序列），而无需进一步训练[1]。

本笔记本是应用机器学习日会议于2022年3月在瑞士洛桑举行的“预测和元学习”研讨会的改编版本。
它包含以下部分：

• 第0部分： 初始设置-导入，下载数据的函数等。
• 第1部分： 预测300个航空公司的乘客数量序列（air数据集）。我们将为每个序列训练一个模型。
• 第2部分： 使用“全局”模型-即同时在所有300个序列上训练的模型。
• 第3部分： 我们将尝试一些迁移学习，并查看如果我们在一个（大）数据集（m4数据集）上训练一些全局模型并在另一个数据集上使用它们会发生什么。
• 第4部分： 我们将在另一个新数据集（m3数据集）上重用第3部分中预训练的模型，并查看它与专门针对该数据集训练的模型相比如何。

不同模型的计算持续时间是在Apple Silicon M2 CPU上运行笔记本时获得的，使用的是Python 3.10.13和Darts 0.27.0。

第0部分：设置

首先，我们需要安装正确的库并进行正确的导入。对于深度学习模型，拥有GPU会有所帮助，但这不是强制性的。

以下两个单元格只需要运行一次。它们安装依赖项并下载所有所需的数据集。

# 安装所需的库
!pip install xlrd
!pip install darts

# 下载数据集
!curl -L https://forecasters.org/data/m3comp/M3C.xls -o m3_dataset.xls  # 使用curl命令下载M3C.xls文件，并保存为m3_dataset.xls
!curl -L https://data.transportation.gov/api/views/xgub-n9bw/rows.csv -o carrier_passengers.csv  # 使用curl命令下载rows.csv文件，并保存为carrier_passengers.csv
!curl -L https://raw.githubusercontent.com/Mcompetitions/M4-methods/master/Dataset/Train/Monthly-train.csv -o m4_monthly.csv  # 使用curl命令下载Monthly-train.csv文件，并保存为m4_monthly.csv
!curl -L https://raw.githubusercontent.com/Mcompetitions/M4-methods/master/Dataset/M4-info.csv -o m4_metadata.csv  # 使用curl命令下载M4-info.csv文件，并保存为m4_metadata.csv

  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100 1716k  100 1716k    0     0  6899k      0 --:--:-- --:--:-- --:--:-- 6949k
  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100 56.3M    0 56.3M    0     0  1747k      0 --:--:--  0:00:33 --:--:-- 2142k
  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100 87.4M  100 87.4M    0     0  26.2M      0  0:00:03  0:00:03 --:--:-- 26.3M
  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100 4233k  100 4233k    0     0  5150k      0 --:--:-- --:--:-- --:--:-- 5163k      0      0 --:--:-- --:--:-- --:--:--     0

现在我们导入所有东西。不要害怕，我们将通过笔记本揭示这些导入的含义 😃

# 设置matplotlib在jupyter notebook中显示图像
%matplotlib inline

# 忽略警告信息
import warnings
warnings.filterwarnings("ignore")

# 导入必要的库
import os
import time
import random
import pandas as pd
import pickle
import numpy as np
from tqdm.auto import tqdm
from datetime import datetime
from itertools import product
import torch
from torch import nn
from typing import List, Tuple, Dict, Optional
from sklearn.preprocessing import MaxAbsScaler
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt

# 导入darts库中的TimeSeries类
from darts import TimeSeries

# 导入darts库中的SmapeLoss类
from darts.utils.losses import SmapeLoss

# 导入darts库中的Scaler类
from darts.dataprocessing.transformers import Scaler

# 导入darts库中的smape函数
from darts.metrics import smape

# 导入darts库中的SeasonalityMode、TrendMode、ModelMode枚举类型
from darts.utils.utils import SeasonalityMode, TrendMode, ModelMode

# 导入darts库中的所有模型
from darts.models import *

我们在这里定义预测的时间范围-对于在这个笔记本中使用的所有（每月）时间序列，我们将对提前18个月的预测感兴趣。我们选择18个月，因为这是M3/M4竞赛中用于月度系列的预测时间范围。

# 定义常量HORIZON为18，表示预测的时间范围为18个单位
HORIZON = 18

数据集加载方法

在这里，我们定义了一些辅助方法来加载我们将要使用的三个数据集：air、m3和m4。

下面的所有方法都返回两个TimeSeries列表：一个是训练系列的列表，另一个是长度为HORIZON的"测试"系列列表。

为了方便起见，所有的系列在这里已经进行了缩放，通过将它们每个乘以一个常数，使得最大值为1。这种缩放对于许多模型的正确工作是必要的（尤其是深度学习模型）。它不会影响sMAPE值，因此我们可以在缩放的系列上评估算法的准确性。在实际应用中，我们需要将Darts的Scaler对象保存在某个地方，以便对预测结果进行逆缩放。

如果您有兴趣看到创建和缩放TimeSeries的示例，可以查看load_m3()函数。

from typing import List, Tuple, Optional
import pandas as pd
import numpy as np
from darts import TimeSeries
from darts.dataprocessing.transformers import Scaler, MaxAbsScaler
from tqdm import tqdm

HORIZON = 18

def load_m3() -> Tuple[List[TimeSeries], List[TimeSeries]]:
    # 读取数据
    df_m3 = pd.read_excel("m3_dataset.xls", "M3Month")
    
    # 构建TimeSeries
    m3_series = []
    for row in tqdm(df_m3.iterrows()):
        s = row[1]
        start_year = int(s["Starting Year"])
        start_month = int(s["Starting Month"])
        values_series = s[6:].dropna()
        
        if start_month == 0:
            continue
        
        start_date = datetime(year=start_year, month=start_month, day=1)
        time_axis = pd.date_range(start_date, periods=len(values_series), freq="M")
        series = TimeSeries.from_times_and_values(
            time_axis, values_series.values
        ).astype(np.float32)
        
        m3_series.append(series)
    
    print("\nM3数据集中有{}个月度时间序列".format(len(m3_series)))
    
    # 划分训练集和测试集
    m3_train = [s[:-HORIZON] for s in m3_series]
    m3_test = [s[-HORIZON:] for s in m3_series]
    
    # 缩放，使最大值为1
    scaler_m3 = Scaler(scaler=MaxAbsScaler())
    m3_train_scaled: List[TimeSeries] = scaler_m3.fit_transform(m3_train)
    m3_test_scaled: List[TimeSeries] = scaler_m3.transform(m3_test)
    
    print(
        "处理完成。M3数据集中有{}个序列，平均训练长度为{}".format(
            len(m3_train_scaled), np.mean([len(s) for s in m3_train_scaled])
        )
    )
    
    return m3_train_scaled, m3_test_scaled

def load_air() -> Tuple[List[TimeSeries], List[TimeSeries]]:
    # 下载csv文件
    df = pd.read_csv("carrier_passengers.csv")
    
    # 提取相关列
    df = df[["data_dte", "carrier", "Total"]]
    
    # 按carrier和date聚合
    df = pd.DataFrame(df.groupby(["carrier", "data_dte"]).sum())
    
    # 将索引移动到列
    df = df.reset_index()
    
    # 按carrier分组，指定时间索引和目标变量
    all_air_series = TimeSeries.from_group_dataframe(
        df, group_cols="carrier", time_col="data_dte", value_cols="Total", freq="MS"
    )
    
    # 划分训练集和测试集
    air_train = []
    air_test = []
    
    for series in all_air_series:
        # 移除序列末尾
        series = series[: pd.Timestamp("2019-12-31")]
        
        # 转换为正确的类型
        series = series.astype(np.float32)
        
        # 提取最长的连续片段
        try:
            series = series.longest_contiguous_slice()
        except:
            continue
        
        # 移除静态协变量
        series = series.with_static_covariates(None)
        
        # 移除长度较短的序列
        if len(series) >= 36 + HORIZON:
            air_train.append(series[:-HORIZON])
            air_test.append(series[-HORIZON:])
    
    # 缩放，使最大值为1
    scaler_air = Scaler(scaler=MaxAbsScaler())
    air_train_scaled: List[TimeSeries] = scaler_air.fit_transform(air_train)
    air_test_scaled: List[TimeSeries] = scaler_air.transform(air_test)
    
    print(
        "处理完成。航空数据集中有{}个序列，平均训练长度为{}".format(
            len(air_train_scaled), np.mean([len(s) for s in air_train_scaled])
        )
    )
    
    return air_train_scaled, air_test_scaled

def load_m4(max_number_series: Optional[int] = None) -> Tuple[List[TimeSeries], List[TimeSeries]]:
    """
    由于数据集的大小，此函数需要大约10分钟的时间。
    如果需要，使用'max_number_series'参数来减少计算时间
    """
    # 读取数据
    df_m4 = pd.read_csv("m4_monthly.csv")
    
    if max_number_series is not None:
        df_m4 = df_m4[:max_number_series]
    
    # 读取元数据
    df_meta = pd.read_csv("m4_metadata.csv")
    df_meta = df_meta.loc[df_meta.SP == "Monthly"]
    
    # 构建TimeSeries
    m4_train = []
    m4_test = []
    
    for row in tqdm(df_m4.iterrows(), total=len(df_m4)):
        s = row[1]
        values_series = s[1:].dropna()
        
        start_date = pd.Timestamp(
            df_meta.loc[df_meta["M4id"] == "M1", "StartingDate"].values[0]
        )
        
        time_axis = pd.date_range(start_date, periods=len(values_series), freq="M")
        series = TimeSeries.from_times_and_values(
            time_axis, values_series.values
        ).astype(np.float32)
        
        # 移除训练样本少于48个的序列
        if len(series) > 48 + HORIZON:
            # 划分训练集和测试集
            m4_train.append(series[:-HORIZON])
            m4_test.append(series[-HORIZON:])
    
    print("\nM4数据集中有{}个月度时间序列".format(len(m4_train)))
    
    # 缩放，使最大值为1
    scaler_m4 = Scaler(scaler=MaxAbsScaler())
    m4_train_scaled: List[TimeSeries] = scaler_m4.fit_transform(m4_train)
    m4_test_scaled: List[TimeSeries] = scaler_m4.transform(m4_test)
    
    print(
        "处理完成。M4数据集中有{}个序列，平均训练长度为{}".format(
            len(m4_train_scaled), np.mean([len(s) for s in m4_train_scaled])
        )
    )
    
    return m4_train_scaled, m4_test_scaled

最后，我们定义了一个方便的函数来告诉我们一堆预测系列的好坏：

# 定义一个函数，输入参数为预测时间序列列表和测试时间序列列表，输出为sMAPE列表
def eval_forecasts(pred_series: List[TimeSeries], test_series: List[TimeSeries]) -> List[float]:
    # 输出计算sMAPE的提示信息
    print("computing sMAPEs...")
    
    # 调用smape函数计算sMAPE列表
    smapes = smape(test_series, pred_series)
    
    # 绘制sMAPE的直方图
    plt.figure()
    plt.hist(smapes, bins=50)
    plt.ylabel("Count")
    plt.xlabel("sMAPE")
    plt.title("Median sMAPE: %.3f" % np.median(smapes))
    plt.show()
    
    # 关闭绘图窗口
    plt.close()
    
    # 返回sMAPE列表
    return smapes

第一部分：在“air”数据集上的本地模型

检查数据

“air”数据集包含从2000年到2019年每个航空公司（或航空公司）飞往或离开美国的乘客人数。

首先，我们可以通过调用上面定义的load_air()函数来加载训练和测试系列。

# 加载空气质量数据集
air_train, air_test = load_air()  # 将数据集分为训练集和测试集

IndexError: The type of your index was not matched.


splitting train/test...


IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.
IndexError: The type of your index was not matched.


scaling series...
done. There are 245 series, with average training length 154.06938775510204

这是一个很好的主意，首先通过可视化一些系列来了解它们的外观。我们可以通过调用series.plot()来绘制一个系列。

# 创建一个包含3行2列的图表，大小为10x10，分辨率为100
figure, ax = plt.subplots(3, 2, figsize=(10, 10), dpi=100)

# 使用enumerate函数遍历一个包含6个元素的列表，同时获取元素的索引和值
for i, idx in enumerate([1, 20, 50, 100, 150, 200]):
    # 获取当前索引对应的坐标轴
    axis = ax[i % 3, i % 2]
    
    # 在当前坐标轴上绘制air_train[idx]的图像
    air_train[idx].plot(ax=axis)
    
    # 在当前坐标轴上添加图例，图例的标签为air_train[idx]的组件
    axis.legend(air_train[idx].components)
    
    # 设置当前坐标轴的标题为空字符串
    axis.set_title("")
    
    # 调整子图的布局，使其紧凑显示
    plt.tight_layout()

我们可以看到大多数系列看起来非常不同，它们甚至有不同的时间轴！例如，有些系列从2001年1月开始，而其他系列则从2010年4月开始。

让我们看看可用的最短火车系列是什么：

min([len(s) for s in air_train])

36

一个有用的评估模型的函数

下面，我们编写一个小函数，以便快速尝试和比较不同的本地模型。我们循环遍历每个系列，拟合模型，然后在测试数据集上进行评估。

⚠️ tqdm是可选的，仅用于帮助显示训练进度（正如您将看到的，当训练300多个时间序列时，可能需要一些时间）。

# 定义函数eval_local_model，接收train_series、test_series、model_cls和kwargs四个参数，返回元组(List[float], float)
def eval_local_model(train_series: List[TimeSeries], test_series: List[TimeSeries], model_cls, **kwargs) -> Tuple[List[float], float]:
    preds = [] # 初始化一个空列表preds，用于存储预测结果
    start_time = time.time() # 记录开始时间
    
    # 遍历train_series中的每一个时间序列
    for series in tqdm(train_series):
        model = model_cls(**kwargs) # 实例化一个模型对象
        model.fit(series) # 对当前时间序列进行拟合
        pred = model.predict(n=HORIZON) # 对当前时间序列进行预测，预测未来HORIZON个时间步长的值
        preds.append(pred) # 将预测结果添加到preds列表中
        elapsed_time = time.time() - start_time # 计算训练模型所花费的时间
    
    smapes = eval_forecasts(preds, test_series) # 对预测结果进行评估，计算smape值
    return smapes, elapsed_time # 返回smape值和训练模型所花费的时间

构建和评估模型

我们现在可以在这个数据集上尝试第一个预测模型。作为第一步，通常最好的做法是看看一个（非常）天真的模型，它盲目地重复训练序列的最后一个值的表现如何。在Darts中，可以使用NaiveSeasonal模型来实现这一点：

naive1_smapes, naive1_time = eval_local_model(air_train, air_test, NaiveSeasonal, K=1)

  0%|          | 0/245 [00:00<?, ?it/s]


computing sMAPEs...

所以最简单的模型给出了一个约为27.2的中位数sMAPE。

我们能否通过利用大多数月度系列具有12个季节性的事实来使用“不那么天真”的模型来取得更好的效果？

# 定义了一个训练数据air_train和测试数据air_test
# NaiveSeasonal是一个季节性预测模型，K=12表示季节性周期为12个月
# 调用eval_local_model函数，传入训练数据air_train、测试数据air_test和季节性预测模型NaiveSeasonal，返回结果为naive12_smapes和naive12_time
naive12_smapes, naive12_time = eval_local_model(air_train, air_test, NaiveSeasonal, K=12)

  0%|          | 0/245 [00:00<?, ?it/s]


computing sMAPEs...

这个更好。让我们尝试指数平滑（默认情况下，对于月度系列，它将使用季节性为12）。

ets_smapes, ets_time = eval_local_model(air_train, air_test, ExponentialSmoothing)

  0%|          | 0/245 [00:00<?, ?it/s]


computing sMAPEs...

中位数模型略优于天真的季节性模型。另一个我们可以快速使用的模型是Theta方法，该方法在M3竞赛中获胜。

# 调用eval_local_model函数，并传入参数air_train, air_test, Theta, theta=1.5
theta_smapes, theta_time = eval_local_model(air_train, air_test, Theta, theta=1.5)

  0%|          | 0/245 [00:00<?, ?it/s]


computing sMAPEs...

ARIMA怎么样？

# 忽略警告信息
warnings.filterwarnings("ignore")  # 使用ARIMA模型进行训练和预测

# 参数air_train为训练数据，air_test为测试数据
# p=12, d=1, q=1为ARIMA模型的参数
arima_smapes, arima_time = eval_local_model(air_train, air_test, ARIMA, p=12, d=1, q=1)

  0%|          | 0/245 [00:00<?, ?it/s]


computing sMAPEs...

或者卡尔曼滤波器？（在Darts中，拟合卡尔曼滤波器使用N4SID系统辨识算法）

kf_smapes, kf_time = eval_local_model(air_train, air_test, KalmanForecaster, dim_x=12)

  0%|          | 0/245 [00:00<?, ?it/s]


computing sMAPEs...

比较模型

下面，我们定义一个函数，可以帮助我们可视化模型在中位数sMAPE和获取预测所需的时间方面相互比较。

def plot_models(method_to_elapsed_times, method_to_smapes):
    # 定义不同形状和颜色的组合
    shapes = ["o", "s", "*"]
    colors = ["tab:blue", "tab:orange", "tab:green", "tab:red", "tab:purple"]
    styles = list(product(shapes, colors))
    
    # 创建一个6*6大小，dpi为100的画布
    plt.figure(figsize=(6, 6), dpi=100)
    
    # 遍历方法到耗时的字典的键值对，i表示索引，method表示方法名，t表示耗时
    for i, method in enumerate(method_to_elapsed_times.keys()):
        t = method_to_elapsed_times[method]
        
        # 取出当前方法对应的形状和颜色
        s = styles[i]
        
        # 绘制一条曲线，横坐标为耗时，纵坐标为当前方法的所有sMAPE的中位数，使用当前方法对应的形状和颜色，标签为方法名，标记大小为13
        plt.semilogx(
            [t],
            [np.median(method_to_smapes[method])],
            s[0],
            color=s[1],
            label=method,
            markersize=13,
        )
    
    # 设置横坐标标签为elapsed time [s]，纵坐标标签为median sMAPE over all series
    # 设置图例的位置为右上角，边框为实线
    plt.xlabel("elapsed time [s]")
    plt.ylabel("median sMAPE over all series")
    plt.legend(bbox_to_anchor=(1.4, 1.0), frameon=True);

# 定义一个字典smapes，包含了不同模型的smape值
smapes = {
    "naive-last": naive1_smapes,  # naive-last模型的smape值
    "naive-seasonal": naive12_smapes,  # naive-seasonal模型的smape值
    "Exponential Smoothing": ets_smapes,  # Exponential Smoothing模型的smape值
    "Theta": theta_smapes,  # Theta模型的smape值
    "ARIMA": arima_smapes,  # ARIMA模型的smape值
    "Kalman Filter": kf_smapes,  # Kalman Filter模型的smape值
}

# 定义一个字典elapsed_times，包含了不同模型的运行时间
elapsed_times = {
    "naive-last": naive1_time,  # naive-last模型的运行时间
    "naive-seasonal": naive12_time,  # naive-seasonal模型的运行时间
    "Exponential Smoothing": ets_time,  # Exponential Smoothing模型的运行时间
    "Theta": theta_time,  # Theta模型的运行时间
    "ARIMA": arima_time,  # ARIMA模型的运行时间
    "Kalman Filter": kf_time,  # Kalman Filter模型的运行时间
}

# 调用plot_models函数，传入elapsed_times和smapes作为参数
plot_models(elapsed_times, smapes)

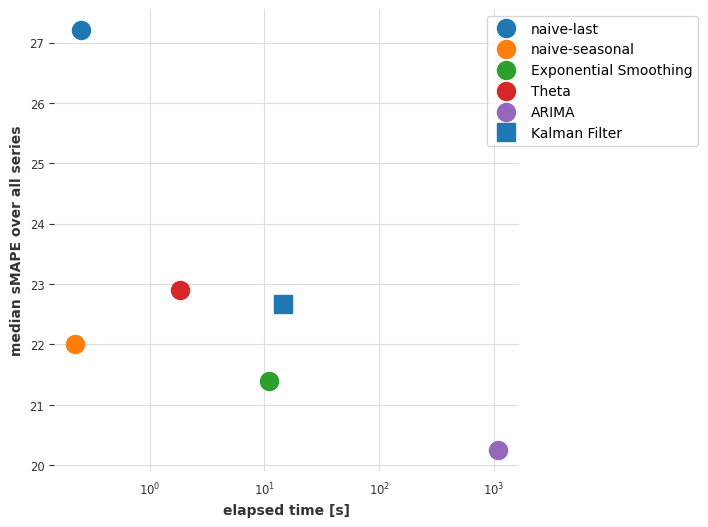
目前的结论

ARIMA模型提供了最好的结果，但它也是（远远）最耗时的模型。指数平滑模型提供了一个有趣的权衡，具有良好的预测准确性和较低的计算成本。我们可以通过考虑全局模型——即仅在所有时间序列上联合训练的模型——来找到更好的折衷方案吗？

第二部分：在air数据集上使用全局模型

在本节中，我们将使用“全局模型”——即一次适用于多个系列的模型。Darts基本上有两种全局模型：

• RegressionModels，它们是类似于sklearn回归模型的包装器（第2.1部分）。
• 基于PyTorch的模型，它们提供了各种深度学习模型（第2.2部分）。

这两种模型都可以通过“制表”数据来训练多个系列——即从所有训练系列中获取许多（输入，输出）子切片，并以监督方式训练机器学习模型以根据输入预测输出。

我们首先定义一个名为eval_global_model()的函数，它的工作方式类似于eval_local_model()，但是针对全局模型。

from typing import List, Tuple
import time

# 定义一个函数eval_global_model，该函数接收train_series、test_series、model_cls和**kwargs四个参数，返回一个元组，包含smapes和elapsed_time两个值
def eval_global_model(train_series: List[TimeSeries], test_series: List[TimeSeries], model_cls, **kwargs) -> Tuple[List[float], float]:
    # 记录开始时间
    start_time = time.time()
    # 创建一个model对象，使用model_cls和**kwargs参数初始化
    model = model_cls(**kwargs)
    # 使用train_series训练model
    model.fit(train_series)
    # 使用train_series预测未来HORIZON个时间步长的数据
    preds = model.predict(n=HORIZON, series=train_series)
    # 计算程序运行时间
    elapsed_time = time.time() - start_time
    # 计算预测值和真实值之间的smape值
    smapes = eval_forecasts(preds, test_series)
    # 返回smapes和elapsed_time两个值
    return smapes, elapsed_time

第2.1部分：使用Darts的RegressionModel。

Darts中的RegressionModel是可以包装任何“scikit-learn兼容”的回归模型以获得预测的预测模型。与深度学习相比，它们代表了很好的“首选”全局模型，因为它们通常没有太多的超参数，并且训练速度更快。此外，Darts还提供了一些“预打包”的回归模型，如LinearRegressionModel和LightGBMModel。

我们现在将使用我们的函数eval_global_models()。在接下来的单元格中，我们将尝试使用一些回归模型，例如：

• LinearRegressionModel
• LightGBMModel
• RegressionModel(some_sklearn_model)

您可以参考API文档了解如何使用它们。

重要的参数是lags和output_chunk_length。它们分别确定模型使用的回顾窗口和“向前看”窗口的长度，并且它们对应于用于训练的输入/输出子片段的长度。例如，lags=24和output_chunk_length=12意味着模型将使用过去的24个滞后值来预测接下来的12个值。在我们的情况下，因为最短的训练序列长度为36，所以我们必须满足lags + output_chunk_length <= 36。（注意，lags也可以是一个整数列表，表示模型要使用的单个滞后值，而不是窗口长度）。

lr_smapes, lr_time = eval_global_model(
    air_train, air_test, LinearRegressionModel, lags=30, output_chunk_length=1
)

computing sMAPEs...

lgbm_smapes, lgbm_time = eval_global_model(
    air_train, air_test, LightGBMModel, lags=30, output_chunk_length=1, objective="mape"
)

[LightGBM] [Warning] Some label values are < 1 in absolute value. MAPE is unstable with such values, so LightGBM rounds them to 1.0 when calculating MAPE.
[LightGBM] [Info] Auto-choosing col-wise multi-threading, the overhead of testing was 0.003476 seconds.
You can set `force_col_wise=true` to remove the overhead.
[LightGBM] [Info] Total Bins 7649
[LightGBM] [Info] Number of data points in the train set: 30397, number of used features: 30
[LightGBM] [Info] Start training from score 0.481005
computing sMAPEs...

rf_smapes, rf_time = eval_global_model(
    air_train, air_test, RandomForest, lags=30, output_chunk_length=1
)

computing sMAPEs...

第2.2部分：使用深度学习

下面，我们将在我们的“air”数据集上训练一个N-BEATS模型。同样，您可以参考API文档了解超参数的文档。
以下超参数应该是一个很好的起点，如果您使用的是（相对较慢的）Colab GPU，则训练应该需要一两分钟。

在训练期间，您可以查看N-BEATS论文。

### Possible N-BEATS hyper-parameters

# Slicing hyper-params:
IN_LEN = 30
OUT_LEN = 4

# Architecture hyper-params:
NUM_STACKS = 20
NUM_BLOCKS = 1
NUM_LAYERS = 2
LAYER_WIDTH = 136
COEFFS_DIM = 11

# Training settings:
LR = 1e-3
BATCH_SIZE = 1024
MAX_SAMPLES_PER_TS = 10
NUM_EPOCHS = 10

现在让我们构建、训练和预测一个N-BEATS模型：

# 设置随机种子以保证结果的可重复性
np.random.seed(42)
torch.manual_seed(42)

start_time = time.time()

# 创建NBEATS模型对象
nbeats_model_air = NBEATSModel(
    input_chunk_length=IN_LEN,  # 输入序列的长度
    output_chunk_length=OUT_LEN,  # 输出序列的长度
    num_stacks=NUM_STACKS,  # 堆叠的数量
    num_blocks=NUM_BLOCKS,  # 每个堆叠中的块的数量
    num_layers=NUM_LAYERS,  # 每个块中的层数
    layer_widths=LAYER_WIDTH,  # 每个层的宽度
    expansion_coefficient_dim=COEFFS_DIM,  # 扩展系数的维度
    loss_fn=SmapeLoss(),  # 损失函数
    batch_size=BATCH_SIZE,  # 批次大小
    optimizer_kwargs={"lr": LR},  # 优化器参数
    pl_trainer_kwargs={
        "enable_progress_bar": True,  # 是否显示进度条
        # 如果你的笔记本在GPU环境中运行，请将此项更改为"gpu"
        "accelerator": "cpu",  # 加速器类型
    },
)

# 使用训练数据训练模型
nbeats_model_air.fit(air_train, num_loader_workers=4, epochs=NUM_EPOCHS)

# 获取预测结果
nb_preds = nbeats_model_air.predict(series=air_train, n=HORIZON)

nbeats_elapsed_time = time.time() - start_time

# 计算预测结果的SMAPE指标
nbeats_smapes = eval_forecasts(nb_preds, air_test)

GPU available: True (mps), used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs

  | Name          | Type             | Params
---------------------------------------------------
0 | criterion     | SmapeLoss        | 0     
1 | train_metrics | MetricCollection | 0     
2 | val_metrics   | MetricCollection | 0     
3 | stacks        | ModuleList       | 525 K 
---------------------------------------------------
523 K     Trainable params
1.9 K     Non-trainable params
525 K     Total params
2.102     Total estimated model params size (MB)



Training: |          | 0/? [00:00<?, ?it/s]


`Trainer.fit` stopped: `max_epochs=10` reached.
GPU available: True (mps), used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs



Predicting: |          | 0/? [00:00<?, ?it/s]


computing sMAPEs...

让我们现在再次看一下我们的错误-时间图：

# 定义一个字典smapes_2，将原有的字典smapes和新的字典合并
smapes_2 = {**smapes, **{
    "Linear Regression": lr_smapes,  # 添加线性回归模型的smape值
    "LGBM": lgbm_smapes,  # 添加LGBM模型的smape值
    "Random Forest": rf_smapes,  # 添加随机森林模型的smape值
    "NBeats": nbeats_smapes,  # 添加NBeats模型的smape值
}}

# 定义一个字典elapsed_times_2，将原有的字典elapsed_times和新的字典合并
elapsed_times_2 = {**elapsed_times, **{
    "Linear Regression": lr_time,  # 添加线性回归模型的运行时间
    "LGBM": lgbm_time,  # 添加LGBM模型的运行时间
    "Random Forest": rf_time,  # 添加随机森林模型的运行时间
    "NBeats": nbeats_elapsed_time,  # 添加NBeats模型的运行时间
}}

# 调用plot_models函数，传入elapsed_times_2和smapes_2作为参数
plot_models(elapsed_times_2, smapes_2)

目前的结论

目前看来，一个在所有系列上联合训练的线性回归模型在准确性和速度之间提供了最佳的权衡。线性回归通常是一个不错的选择！

我们的深度学习模型 N-BEATS 表现不佳。请注意，我们还没有尝试明确地调整它以解决这个问题，这样做可能会产生更准确的结果。不过，我们将不花时间来调整它，而是在下一部分中看看它是否可以通过在完全不同的数据集上进行训练来取得更好的效果。

第三部分：在 m4 数据集上训练 N-BEATS 模型并用它来预测 air 数据集

当深度学习模型在大规模数据集上进行训练时，通常会表现更好。让我们尝试加载 M4 数据集中的所有 48,000 个月度时间序列，并再次在这个更大的数据集上训练我们的模型。

# 调用load_m4函数，将返回的结果分别赋值给m4_train和m4_test
m4_train, m4_test = load_m4()

  0%|          | 0/48000 [00:00<?, ?it/s]



There are 47087 monthly series in the M3 dataset
scaling...
done. There are 47087 series, with average training length 201.25202285131778

我们可以从之前的相同超参数开始。

由于48,000个M4训练序列的平均长度约为200个时间步长，我们将得到约10M个训练样本。由于训练样本数量如此之多，每个epoch的训练时间会太长。因此，在调用fit()时，我们将限制每个序列使用的训练样本数量。这是通过使用参数max_samples_per_ts来实现的。我们添加一个新的超参数MAX_SAMPLES_PER_TS来捕捉这个限制。

由于M4训练序列都稍微更长一些，我们还可以使用稍长的input_chunk_length。

# 切片超参数：IN_LEN = 36  # 输入序列长度
# OUT_LEN = 4  # 输出序列长度
IN_LEN = 36
OUT_LEN = 4
# 架构超参数：NUM_STACKS = 20  # 堆叠的LSTM层数
NUM_BLOCKS = 1  # 每个堆叠的LSTM块数
NUM_LAYERS = 2  # 每个LSTM块中的层数
LAYER_WIDTH = 136  # 每个LSTM层的神经元数
COEFFS_DIM = 11  # 线性层的输出维度

# 训练设置：LR = 1e-3  # 学习率
BATCH_SIZE = 1024  # 批量大小
MAX_SAMPLES_PER_TS = (
    10  # <-- new parameter, limiting the number of training samples per series
)
NUM_EPOCHS = 5  # 训练轮数

# 设置随机种子，保证结果的可重复性
np.random.seed(42)
torch.manual_seed(42)

# 创建NBEATS模型
nbeats_model_m4 = NBEATSModel(
    input_chunk_length=IN_LEN,  # 输入时间序列的长度
    output_chunk_length=OUT_LEN,  # 输出时间序列的长度
    batch_size=BATCH_SIZE,  # 批处理大小
    num_stacks=NUM_STACKS,  # 堆叠的数量
    num_blocks=NUM_BLOCKS,  # 块的数量
    num_layers=NUM_LAYERS,  # 层的数量
    layer_widths=LAYER_WIDTH,  # 每层的宽度
    expansion_coefficient_dim=COEFFS_DIM,  # 扩展系数的维度
    loss_fn=SmapeLoss(),  # 损失函数
    optimizer_kwargs={"lr": LR},  # 优化器的参数
    pl_trainer_kwargs={
        "enable_progress_bar": True,  # 是否显示进度条
        # 如果你的笔记本在GPU环境中运行，请将此项更改为"gpu"
        "accelerator": "cpu",
    },
)

# 训练模型
nbeats_model_m4.fit(
    m4_train,  # 训练数据
    num_loader_workers=4,  # 数据加载器的工作线程数
    epochs=NUM_EPOCHS,  # 训练的轮数
    max_samples_per_ts=MAX_SAMPLES_PER_TS,  # 每个时间序列的最大样本数
)

GPU available: True (mps), used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs

  | Name          | Type             | Params
---------------------------------------------------
0 | criterion     | SmapeLoss        | 0     
1 | train_metrics | MetricCollection | 0     
2 | val_metrics   | MetricCollection | 0     
3 | stacks        | ModuleList       | 543 K 
---------------------------------------------------
541 K     Trainable params
1.9 K     Non-trainable params
543 K     Total params
2.173     Total estimated model params size (MB)



Training: |          | 0/? [00:00<?, ?it/s]


`Trainer.fit` stopped: `max_epochs=5` reached.





NBEATSModel(generic_architecture=True, num_stacks=20, num_blocks=1, num_layers=2, layer_widths=136, expansion_coefficient_dim=11, trend_polynomial_degree=2, dropout=0.0, activation=ReLU, input_chunk_length=36, output_chunk_length=4, batch_size=1024, loss_fn=SmapeLoss(), optimizer_kwargs={'lr': 0.001}, pl_trainer_kwargs={'enable_progress_bar': True, 'accelerator': 'cpu'})

我们现在可以使用我们训练过的M4模型来预测航空乘客系列。由于我们在这里使用模型进行"元学习"（或迁移学习），我们只会计时推理部分。

# 记录开始时间
start_time = time.time()

# 使用nbeats模型对air_train数据进行预测，预测结果保存在preds中
preds = nbeats_model_m4.predict(series=air_train, n=HORIZON)  # 获取预测结果

# 计算nbeats模型的运行时间
nbeats_m4_elapsed_time = time.time() - start_time

# 使用eval_forecasts函数计算nbeats模型的预测结果与air_test数据的sMAPE值
nbeats_m4_smapes = eval_forecasts(preds, air_test)

GPU available: True (mps), used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs



Predicting: |          | 0/? [00:00<?, ?it/s]


computing sMAPEs...

# 将smapes_2和{"N-BEATS (M4-trained)": nbeats_m4_smapes}合并为一个新的字典smapes_3
smapes_3 = {**smapes_2, **{"N-BEATS (M4-trained)": nbeats_m4_smapes}}

# 将elapsed_times_2和{"N-BEATS (M4-trained)": nbeats_m4_elapsed_time}合并为一个新的字典elapsed_times_3
elapsed_times_3 = {**elapsed_times_2, **{"N-BEATS (M4-trained)": nbeats_m4_elapsed_time}}

# 调用plot_models函数，传入elapsed_times_3和smapes_3作为参数
plot_models(elapsed_times_3, smapes_3)

目前的结论

虽然在准确性方面并不是绝对最好的，但我们在m4上训练的N-BEATS模型达到了竞争力的准确性。这是非常了不起的，因为这个模型没有在我们要求它预测的任何air系列上进行过训练！使用N-BEATS进行预测的步骤比我们使用ARIMA进行拟合-预测步骤快1000倍以上，也比线性回归快。

只是为了好玩，我们还可以手动检查一下这个模型在另一个系列上的表现–例如，在darts.datasets中可用的月度牛奶产量系列上。

# 导入所需的库
from darts.datasets import MonthlyMilkDataset


# 加载数据集
series = MonthlyMilkDataset().load().astype(np.float32)

# 划分训练集和验证集
train, val = series[:-24], series[-24:]

# 使用MaxAbsScaler进行数据归一化
scaler = Scaler(scaler=MaxAbsScaler())
train = scaler.fit_transform(train)
val = scaler.transform(val)
series = scaler.transform(series)

# 使用nbeats_model_m4模型对训练集进行预测
pred = nbeats_model_m4.predict(series=train, n=24)

# 绘制实际数据和预测数据的图像
series.plot(label="actual")
pred.plot(label="0-shot forecast")

GPU available: True (mps), used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs



Predicting: |          | 0/? [00:00<?, ?it/s]





<Axes: xlabel='Month'>

现在让我们尝试在M4数据集上训练其他全局模型，以查看是否可以获得类似的结果。下面，我们将在完整的m4数据集上训练一些RegressionModel。这可能会相当慢。为了更快地训练，我们可以使用例如random.choices(m4_train, k=5000)而不是m4_train来限制训练集的大小。我们还可以指定足够小的max_samples_per_ts值，以限制训练样本的数量。

# 设置随机种子random.seed(42)
# Set the random seed to 42

# 创建线性回归模型对象，设置lags参数为30，output_chunk_length参数为1
# Create a linear regression model object with lags parameter set to 30 and output_chunk_length parameter set to 1
lr_model_m4 = LinearRegressionModel(lags=30, output_chunk_length=1)

# 使用训练数据拟合模型
# Fit the model using the training data
lr_model_m4.fit(m4_train)

# 记录开始时间
# Record the start time
tic = time.time()

# 使用训练好的模型对air_train数据进行预测，预测未来HORIZON个时间步长的值
# Use the trained model to predict the values for air_train data for the next HORIZON time steps
preds = lr_model_m4.predict(n=HORIZON, series=air_train)

# 计算线性回归模型预测的时间
# Calculate the time taken for linear regression model predictions
lr_time_transfer = time.time() - tic

# 计算线性回归模型的SMAPE评估指标
# Calculate the SMAPE evaluation metric for the linear regression model
lr_smapes_transfer = eval_forecasts(preds, air_test)

computing sMAPEs...

# 设置随机种子
random.seed(42)

# 创建LightGBM模型对象，设置lags为30，output_chunk_length为1，目标函数为mape
lgbm_model_m4 = LightGBMModel(lags=30, output_chunk_length=1, objective="mape")

# 使用m4_train数据训练模型
lgbm_model_m4.fit(m4_train)

# 记录开始时间
tic = time.time()

# 使用训练好的模型对air_train数据进行预测，预测的长度为HORIZON
preds = lgbm_model_m4.predict(n=HORIZON, series=air_train)

# 计算预测时间
lgbm_time_transfer = time.time() - tic

# 计算预测结果的smape值
lgbm_smapes_transfer = eval_forecasts(preds, air_test)

[LightGBM] [Warning] Some label values are < 1 in absolute value. MAPE is unstable with such values, so LightGBM rounds them to 1.0 when calculating MAPE.
[LightGBM] [Info] Auto-choosing row-wise multi-threading, the overhead of testing was 0.097573 seconds.
You can set `force_row_wise=true` to remove the overhead.
And if memory is not enough, you can set `force_col_wise=true`.
[LightGBM] [Info] Total Bins 7650
[LightGBM] [Info] Number of data points in the train set: 8063744, number of used features: 30
[LightGBM] [Info] Start training from score 0.722222
computing sMAPEs...

最后，让我们也将这些新的结果绘制出来。

# 定义一个字典smapes_4，包含了smapes_3和lr_smapes_transfer、lgbm_smapes_transfer两个键值对
smapes_4 = {**smapes_3, **{"Linear Reg (M4-trained)": lr_smapes_transfer, "LGBM (M4-trained)": lgbm_smapes_transfer}}

# 定义一个字典elapsed_times_4，包含了elapsed_times_3和lr_time_transfer、lgbm_time_transfer两个键值对
elapsed_times_4 = {**elapsed_times_3, **{"Linear Reg (M4-trained)": lr_time_transfer, "LGBM (M4-trained)": lgbm_time_transfer}}

# 调用plot_models函数，传入elapsed_times_4和smapes_4作为参数
plot_models(elapsed_times_4, smapes_4)

第四部分和回顾：在M3数据集上使用相同的模型。

好的，现在，我们在航空乘客数据集上运气好吗？让我们通过在一个新的数据集上重复整个过程来看看 😃 你会发现实际上只需要很少的代码。作为一个新的数据集，我们将使用"M3"，其中包含来自M3竞赛的大约1,400个月度系列。

# 调用load_m3函数，将返回的结果分别赋值给m3_train和m3_test
m3_train, m3_test = load_m3()

building M3 TimeSeries...



0it [00:00, ?it/s]



There are 1399 monthly series in the M3 dataset
splitting train/test...
scaling...
done. There are 1399 series, with average training length 100.30092923516797

# 使用NaiveSeasonal模型评估m3_train和m3_test数据集
naive1_smapes_m3, naive1_time_m3 = eval_local_model(m3_train, m3_test, NaiveSeasonal, K=1)

  0%|          | 0/1399 [00:00<?, ?it/s]


computing sMAPEs...

# 调用函数eval_local_model，输入参数为m3_train, m3_test, NaiveSeasonal和K=12
naive12_smapes_m3, naive12_time_m3 = eval_local_model(m3_train, m3_test, NaiveSeasonal, K=12)

  0%|          | 0/1399 [00:00<?, ?it/s]


computing sMAPEs...

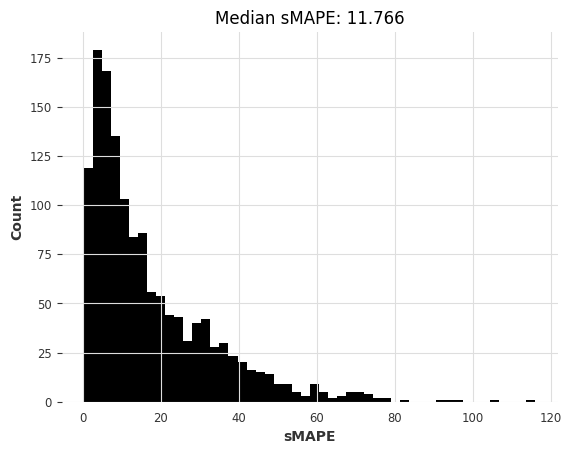
# 调用eval_local_model函数，传入训练数据m3_train、测试数据m3_test和ExponentialSmoothing模型
ets_smapes_m3, ets_time_m3 = eval_local_model(m3_train, m3_test, ExponentialSmoothing)

  0%|          | 0/1399 [00:00<?, ?it/s]


computing sMAPEs...

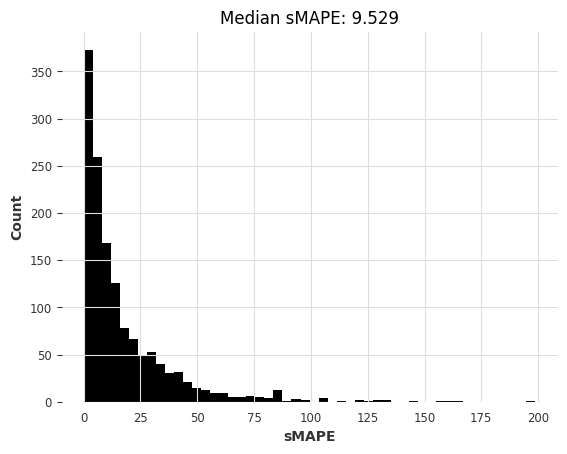
# 调用 eval_local_model 函数，传入训练数据 m3_train、测试数据 m3_test 和模型参数 Theta
theta_smapes_m3, theta_time_m3 = eval_local_model(m3_train, m3_test, Theta)

  0%|          | 0/1399 [00:00<?, ?it/s]


computing sMAPEs...

# 忽略警告信息
warnings.filterwarnings("ignore")  # ARIMA 会生成很多警告信息

# 注意：在这里使用 q=1 会导致某些序列出现错误，因此我们使用 q=0

# 调用 eval_local_model 函数，使用 ARIMA 模型进行训练和预测
arima_smapes_m3, arima_time_m3 = eval_local_model(m3_train, m3_test, ARIMA, p=12, d=1, q=0)

  0%|          | 0/1399 [00:00<?, ?it/s]


computing sMAPEs...

# 调用eval_local_model函数，传入m3_train、m3_test、KalmanForecaster类和dim_x=12作为参数
kf_smapes_m3, kf_time_m3 = eval_local_model(m3_train, m3_test, KalmanForecaster, dim_x=12)

  0%|          | 0/1399 [00:00<?, ?it/s]


computing sMAPEs...

# 调用eval_global_model函数，传入m3_train和m3_test作为训练集和测试集，使用LinearRegressionModel模型，lags为30，output_chunk_length为1
lr_smapes_m3, lr_time_m3 = eval_global_model(m3_train, m3_test, LinearRegressionModel, lags=30, output_chunk_length=1)

computing sMAPEs...

# 调用eval_global_model函数，传入参数
lgbm_smapes_m3, lgbm_time_m3 = eval_global_model(m3_train, m3_test, LightGBMModel, lags=35, output_chunk_length=1, objective="mape")

[LightGBM] [Warning] Some label values are < 1 in absolute value. MAPE is unstable with such values, so LightGBM rounds them to 1.0 when calculating MAPE.
[LightGBM] [Info] Auto-choosing col-wise multi-threading, the overhead of testing was 0.004819 seconds.
You can set `force_col_wise=true` to remove the overhead.
[LightGBM] [Info] Total Bins 8925
[LightGBM] [Info] Number of data points in the train set: 91356, number of used features: 35
[LightGBM] [Info] Start training from score 0.771293
computing sMAPEs...

# 开始计时
start_time = time.time()

# 使用预训练的 N-BEATS 模型对 m3_train 数据集进行预测，预测的时间范围为 HORIZON
preds = nbeats_model_m4.predict(series=m3_train, n=HORIZON)  # 获取预测结果

# 计算预测所花费的时间
nbeats_m4_elapsed_time_m3 = time.time() - start_time

# 对预测结果进行评估，计算 SMAPE 值
nbeats_m4_smapes_m3 = eval_forecasts(preds, m3_test)

GPU available: True (mps), used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs



Predicting: |          | 0/? [00:00<?, ?it/s]


computing sMAPEs...

# 开始计时
start_time = time.time()

# 使用预训练的线性回归模型获取预测结果
preds = lr_model_m4.predict(series=m3_train, n=HORIZON)

# 获取预测结果的耗时
lr_m4_elapsed_time_m3 = time.time() - start_time

# 计算预测结果的SMAPE值
lr_m4_smapes_m3 = eval_forecasts(preds, m3_test)

computing sMAPEs...

# 获取使用预训练的LightGBM模型的预测结果
start_time = time.time()  # 记录开始时间
preds = lgbm_model_m4.predict(series=m3_train, n=HORIZON)  # 获取预测结果
lgbm_m4_elapsed_time_m3 = time.time() - start_time  # 计算预测时间

# 计算预测结果的SMAPE评估指标
lgbm_m4_smapes_m3 = eval_forecasts(preds, m3_test)

computing sMAPEs...

# 定义了两个字典，分别存储了模型的运行时间和模型的SMAPE指标
smapes_m3 = {
    "naive-last": naive1_smapes_m3,  # 简单滞后模型的SMAPE指标
    "naive-seasonal": naive12_smapes_m3,  # 季节性滞后模型的SMAPE指标
    "Exponential Smoothing": ets_smapes_m3,  # 指数平滑模型的SMAPE指标
    "ARIMA": arima_smapes_m3,  # ARIMA模型的SMAPE指标
    "Theta": theta_smapes_m3,  # Theta模型的SMAPE指标
    "Kalman filter": kf_smapes_m3,  # 卡尔曼滤波模型的SMAPE指标
    "Linear Regression": lr_smapes_m3,  # 线性回归模型的SMAPE指标
    "LGBM": lgbm_smapes_m3,  # LGBM模型的SMAPE指标
    "N-BEATS (M4-trained)": nbeats_m4_smapes_m3,  # N-BEATS模型在M4数据集上训练的SMAPE指标
    "Linear Reg (M4-trained)": lr_m4_smapes_m3,  # 线性回归模型在M4数据集上训练的SMAPE指标
    "LGBM (M4-trained)": lgbm_m4_smapes_m3,  # LGBM模型在M4数据集上训练的SMAPE指标
}

times_m3 = {
    "naive-last": naive1_time_m3,  # 简单滞后模型的运行时间
    "naive-seasonal": naive12_time_m3,  # 季节性滞后模型的运行时间
    "Exponential Smoothing": ets_time_m3,  # 指数平滑模型的运行时间
    "ARIMA": arima_time_m3,  # ARIMA模型的运行时间
    "Theta": theta_time_m3,  # Theta模型的运行时间
    "Kalman filter": kf_time_m3,  # 卡尔曼滤波模型的运行时间
    "Linear Regression": lr_time_m3,  # 线性回归模型的运行时间
    "LGBM": lgbm_time_m3,  # LGBM模型的运行时间
    "N-BEATS (M4-trained)": nbeats_m4_elapsed_time_m3,  # N-BEATS模型在M4数据集上训练的运行时间
    "Linear Reg (M4-trained)": lr_m4_elapsed_time_m3,  # 线性回归模型在M4数据集上训练的运行时间
    "LGBM (M4-trained)": lgbm_m4_elapsed_time_m3,  # LGBM模型在M4数据集上训练的运行时间
}

# 调用plot_models函数，传入times_m3和smapes_m3两个字典作为参数
plot_models(times_m3, smapes_m3)

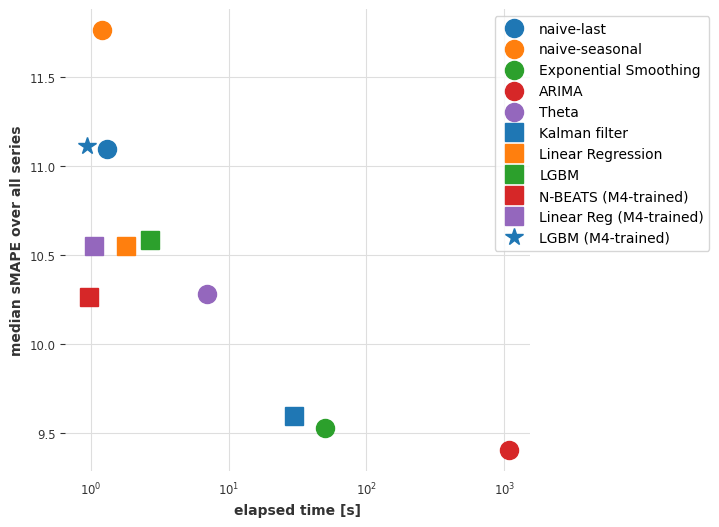
结论

迁移学习和元学习在时间序列预测中无疑是一个有趣的现象，目前还没有得到充分探索。它何时成功？何时失败？微调是否有帮助？何时应该使用？这些问题中的许多仍然需要探索，但我们希望已经展示了使用Darts模型进行探索是相当容易的。

那么，对于您的情况来说，哪种方法最好？一如既往，这取决于情况。如果您主要处理的是具有足够历史记录的孤立系列，传统方法如ARIMA将为您提供很大帮助。即使在较大的数据集上，如果计算能力不是太大的问题，它们也可以作为有趣的开箱即用选项。另一方面，如果您处理的是更多的系列或更高维度的系列，机器学习方法和全局模型通常是更好的选择。它们可以捕捉到不同时间序列范围内的模式，并且通常运行速度更快。在这个类别中，不要低估基于线性回归的模型！如果您有理由相信您需要捕捉更复杂的模式，或者如果推理速度对您来说真的很重要，请尝试使用深度学习方法。N-BEATS已经证明了其在元学习中的价值[1]，但这也可能适用于其他模型。

[1] Oreshkin等人，“具有零样本时间序列预测应用的元学习框架”，2020年，https://arxiv.org/abs/2002.02887