伯努利朴素贝叶斯详解:初学者的可视化指南与代码示例
分类算法通过是/否概率解锁预测能力

本文中的所有插图均由作者创建,结合了来自Canva Pro的许可设计元素。
与虚拟分类器或KNN的基于相似性的推理的基线方法不同,朴素贝叶斯利用概率理论。它结合了每个“线索”(或特征)的个体概率来做出最终预测。这种直接而强大的方法在各种机器学习应用中被证明是不可或缺的。
定义
朴素贝叶斯是一种使用概率对数据进行分类的机器学习算法。它基于贝叶斯定理,这是一个计算条件概率的公式。“朴素”部分指的是它的关键假设:它将所有特征视为相互独立,即使在现实中它们可能并不是。虽然这种简化通常不现实,但它大大降低了计算复杂性,并在许多实际场景中表现良好。

朴素贝叶斯方法是机器学习中使用概率作为基础的简单算法。
朴素贝叶斯分类器的主要类型
有三种主要的朴素贝叶斯分类器。这些类型之间的主要区别在于它们对特征分布的假设:
- 伯努利朴素贝叶斯: 适用于二元/布尔特征。它假设每个特征是一个二值(0/1)变量。
- 多项式朴素贝叶斯:通常用于离散计数。它常用于文本分类,其中特征可能是单词计数。
- 高斯朴素贝叶斯:假设连续特征遵循正态分布。
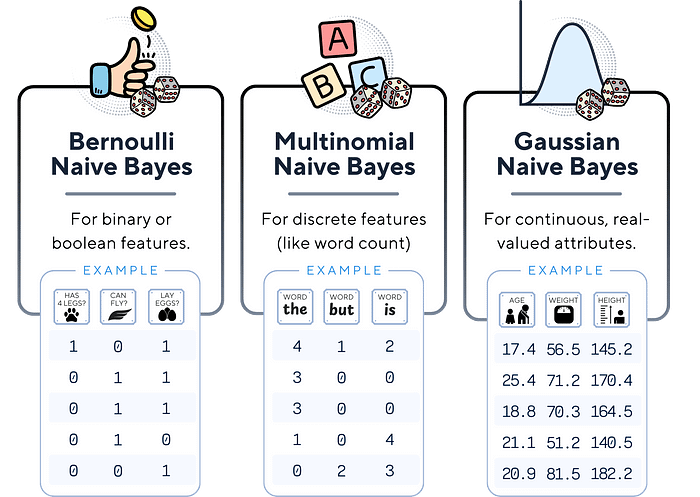
伯努利朴素贝叶斯假设二元数据,多项式朴素贝叶斯处理离散计数,高斯朴素贝叶斯则处理连续数据,假设其服从正态分布。
最简单的朴素贝叶斯模型是伯努利朴素贝叶斯。其名称中的“伯努利”源于对每个特征是二值的假设。
使用的数据集
在整篇文章中,我们将使用这个人工高尔夫数据集(灵感来源于[1])作为示例。这个数据集根据天气条件预测一个人是否会打高尔夫。
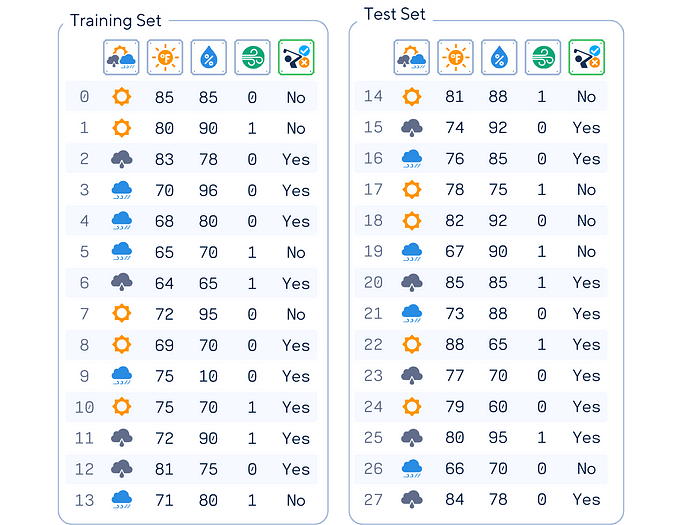
列:‘展望’,‘温度’(华氏度),‘湿度’(%),‘风’和‘游戏’(目标特征)
# 导入数据集 #
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
import numpy as np
dataset_dict = {
'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}
df = pd.DataFrame(dataset_dict)
# 对'Outlook'列进行独热编码
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
# 将'Windy'(布尔值)和'Play'(二进制)列转换为二进制指示符
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)
# 设置特征矩阵X和目标向量y
X, y = df.drop(columns='Play'), df['Play']
# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
print(pd.concat([X_train, y_train], axis=1), end='\n\n')
print(pd.concat([X_test, y_test], axis=1))
我们将稍微调整它以适应伯努利朴素贝叶斯,通过将我们的特征转换为二进制。

由于所有数据都必须以 0 和 1 格式表示,因此“天气状况”采用独热编码,而温度则分为 ≤ 80 和 > 80。同样,湿度分为 ≤ 75 和 > 75。
# One-hot encode the categorized columns and drop them after, but do it separately for training and test sets
# Define categories for 'Temperature' and 'Humidity' for training set
X_train['Temperature'] = pd.cut(X_train['Temperature'], bins=[0, 80, 100], labels=['Warm', 'Hot'])
X_train['Humidity'] = pd.cut(X_train['Humidity'], bins=[0, 75, 100], labels=['Dry', 'Humid'])
# Similarly, define for the test set
X_test['Temperature'] = pd.cut(X_test['Temperature'], bins=[0, 80, 100], labels=['Warm', 'Hot'])
X_test['Humidity'] = pd.cut(X_test['Humidity'], bins=[0, 75, 100], labels=['Dry', 'Humid'])
# One-hot encode the categorized columns
one_hot_columns_train = pd.get_dummies(X_train[['Temperature', 'Humidity']], drop_first=True, dtype=int)
one_hot_columns_test = pd.get_dummies(X_test[['Temperature', 'Humidity']], drop_first=True, dtype=int)
# Drop the categorized columns from training and test sets
X_train = X_train.drop(['Temperature', 'Humidity'], axis=1)
X_test = X_test.drop(['Temperature', 'Humidity'], axis=1)
# Concatenate the one-hot encoded columns with the original DataFrames
X_train = pd.concat([one_hot_columns_train, X_train], axis=1)
X_test = pd.concat([one_hot_columns_test, X_test], axis=1)
print(pd.concat([X_train, y_train], axis=1), '\n')
print(pd.concat([X_test, y_test], axis=1))
主要机制
伯努利朴素贝叶斯运作在每个特征是0或1的数据上。
- 计算训练数据中每个类别的概率。
- 对于每个特征和类别,计算在给定类别下特征为1和0的概率。
- 对于一个新实例:对于每个类别,将其概率乘以该类别每个特征值(0或1)的概率。
- 预测具有最高结果概率的类别。
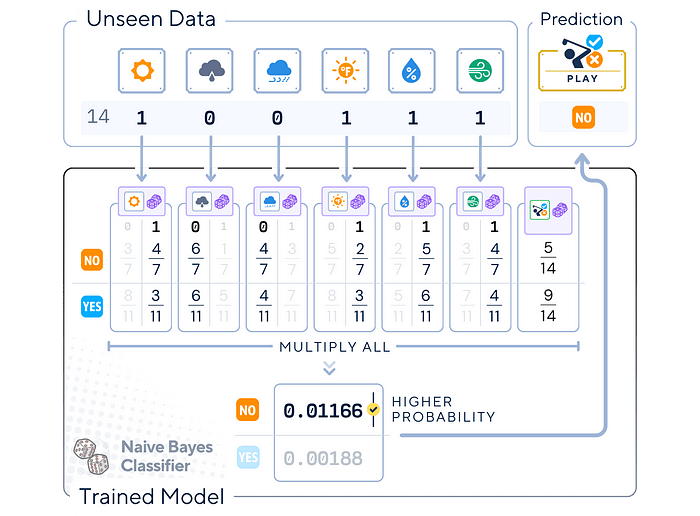
对于我们的高尔夫数据集,伯努利朴素贝叶斯分类器查看每个特征在每个类别(是&否)发生的概率,然后根据哪个类别具有更高的机会来做出决策。
训练步骤
伯努利朴素贝叶斯的训练过程涉及从训练数据中计算概率:
- 类别概率计算:对于每个类别,计算其概率: (该类别中的实例数量) / (实例总数量)
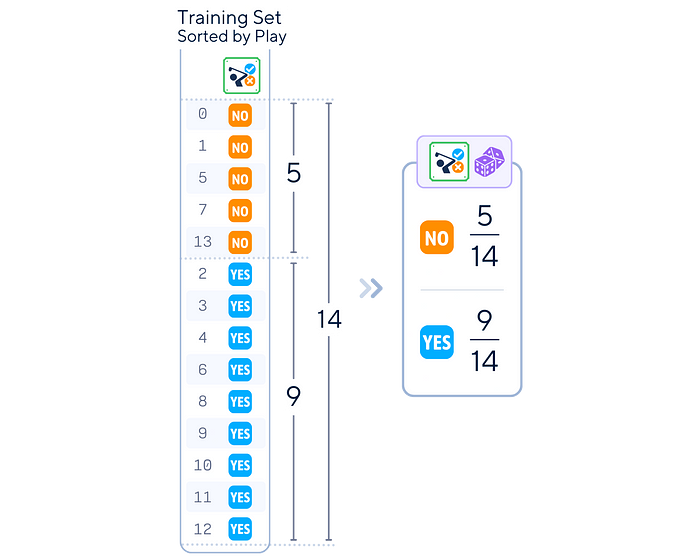
在我们的高尔夫示例中,算法会计算高尔夫的整体参与频率。
from fractions import Fraction
def calc_target_prob(attr):
total_counts = attr.value_counts().sum()
prob_series = attr.value_counts().apply(lambda x: Fraction(x, total_counts).limit_denominator())
return prob_series
print(calc_target_prob(y_train))
2.特征概率计算:对于每个特征和每个类别,计算:
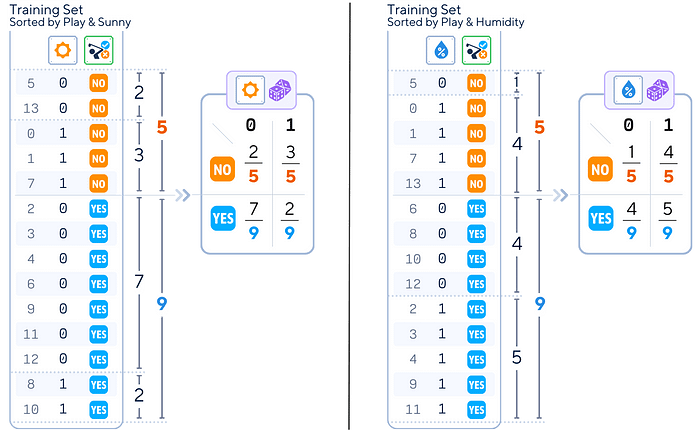
对于每种天气情况(例如,晴天),在晴天时高尔夫的参与频率,以及在晴天时不参与高尔夫的频率。
from fractions import Fraction
def sort_attr_label(attr, lbl):
return (pd.concat([attr, lbl], axis=1)
.sort_values([attr.name, lbl.name])
.reset_index()
.rename(columns={'index': 'ID'})
.set_index('ID'))
def calc_feature_prob(attr, lbl):
total_classes = lbl.value_counts()
counts = pd.crosstab(attr, lbl)
prob_df = counts.apply(lambda x: [Fraction(c, total_classes[x.name]).limit_denominator() for c in x])
return prob_df
print(sort_attr_label(y_train, X_train['sunny']))
print(calc_feature_prob(X_train['sunny'], y_train))
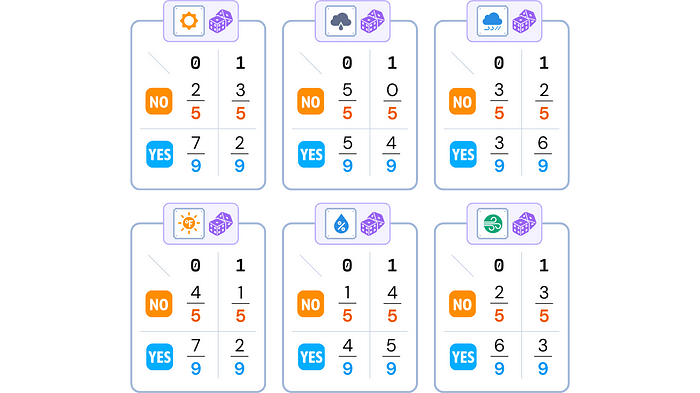
对所有其他特征应用相同的过程。
for col in X_train.columns:
print(calc_feature_prob(X_train[col], y_train), "\n")
3. 平滑(可选):在每个概率计算的分子和分母中添加一个小值(通常为 1),以避免零概率
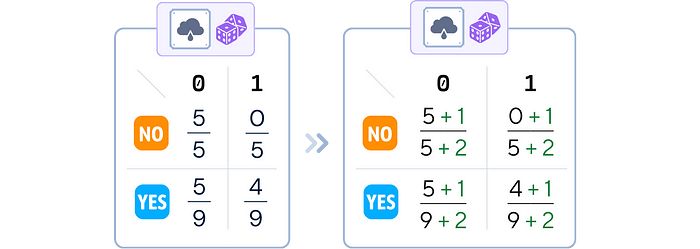
我们对所有分子加1,对所有分母加2,以保持总的类概率为1。
# 在sklearn中,上述所有过程在这个'fit'方法中进行了总结:
from sklearn.naive_bayes import BernoulliNB
nb_clf = BernoulliNB(alpha=1)
nb_clf.fit(X_train, y_train)
4. 存储结果: 保存所有计算出的概率以供分类时使用。
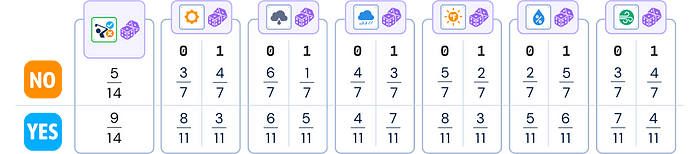
平滑已经应用于所有特征概率。我们将使用这些表来进行预测。
分类步骤
给定一个特征为0或1的新实例:
- 概率集合: 对于每个可能的类别:
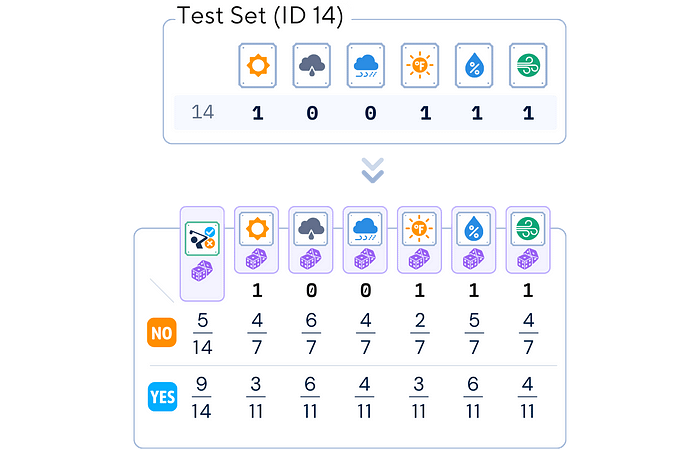
对于ID 14,我们选择每个特征发生的概率(0或1)。
2. 评分计算与预测: 对于每个类别:

在将类别概率与所有特征概率相乘后,我们选择得分更高的类别。
y_pred = nb_clf.predict(X_test)
print(y_pred)
评估步骤
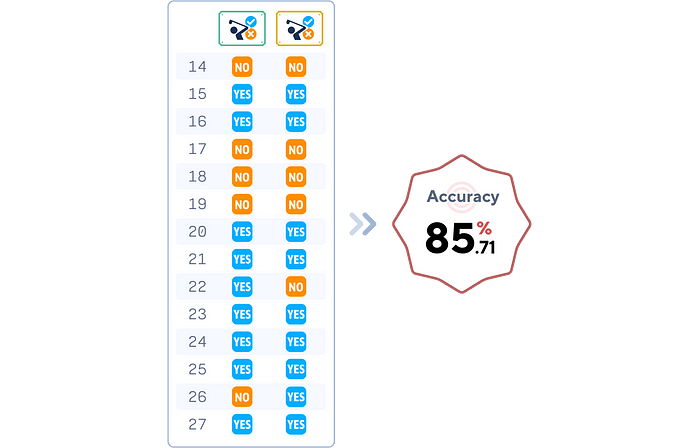
这个简单的概率模型在这个简单的数据集上表现出很高的准确性。
# 评估分类器
print(f"准确率: {accuracy_score(y_test, y_pred)}")
关键参数
伯努利朴素贝叶斯有几个重要的参数:
- Alpha (α): 这是平滑参数。它为每个特征添加一个小的计数,以防止零概率。默认值通常是 1.0(拉普拉斯平滑),正如之前所示。
- 二值化:如果你的特征还不是二进制的,这个阈值将它们转换为二进制。超过这个阈值的任何值变为1,低于这个阈值的任何值变为0\。
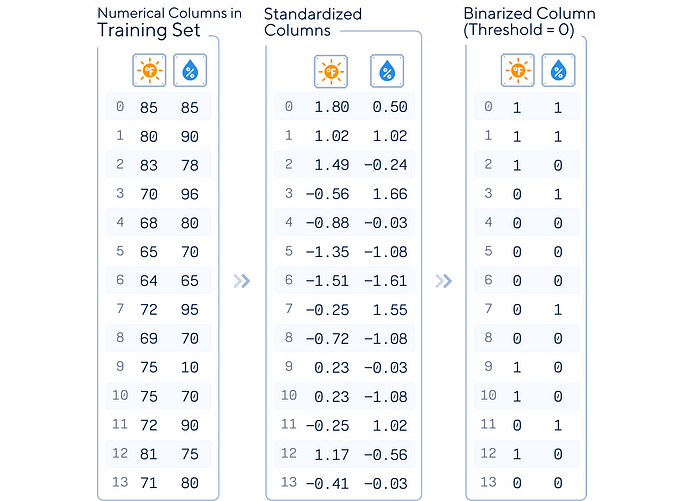
对于scikit-learn中的BernoulliNB,数值特征通常被标准化,而不是手动二值化。模型随后内部将这些标准化的值转换为二进制,通常使用0(均值)作为阈值。
3. 拟合先验:是否学习类别先验概率或假设均匀先验(50/50)。
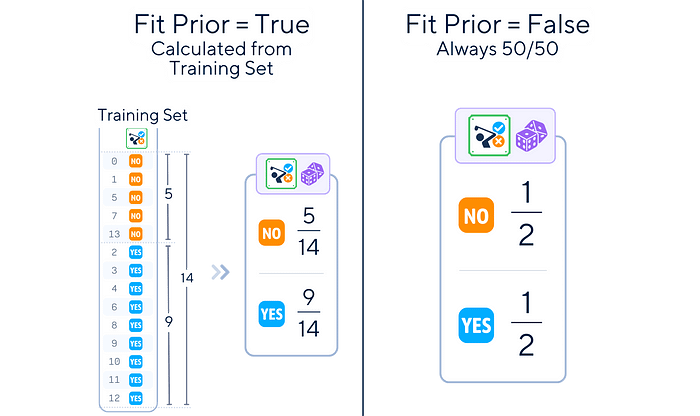
对于我们的高尔夫数据集,我们可能从默认的 α=1.0 开始,不进行二值化(因为我们已经将特征转换为二进制),并设置 fit_prior=True。
优点 & 缺点
与机器学习中的任何算法一样,伯努利朴素贝叶斯也有其优点和局限性。
优点:
- 简单性:易于实现和理解。
- 效率:训练和预测速度快,适用于大特征空间。
- 小数据集的表现:即使在有限的训练数据下也能表现良好。
- 处理高维数据:在许多特征中表现良好,尤其是在文本分类中。
缺点:
- 独立性假设: 假设所有特征是相互独立的,但在现实数据中通常不成立。
- 仅限于二进制特征:在其纯粹形式中,仅适用于二进制数据。
- 对输入数据的敏感性:对特征的二值化方式可能十分敏感。
- 零频率问题:在没有平滑处理的情况下,零概率可能会严重影响预测。
最终备注
伯努利朴素贝叶斯分类器是一种简单但强大的机器学习算法,适用于二元分类。它在文本分析和垃圾邮件检测中表现出色,特征通常是二元的。这个概率模型以其速度和效率而闻名,在小型数据集和高维空间中表现良好。
尽管它天真地假设特征相互独立,但在准确性上常常与更复杂的模型相媲美。伯努利朴素贝叶斯是一个出色的基准和实时分类工具。
🌟 伯努利朴素贝叶斯简化版
# 导入所需的库
import pandas as pd
from sklearn.naive_bayes import BernoulliNB
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# 加载数据集
dataset_dict = {
'Outlook': ['sunny', 'sunny', 'overcast', 'rainy', 'rainy', 'rainy', 'overcast', 'sunny', 'sunny', 'rainy', 'sunny', 'overcast', 'overcast', 'rainy', 'sunny', 'overcast', 'rainy', 'sunny', 'sunny', 'rainy', 'overcast', 'rainy', 'sunny', 'overcast', 'sunny', 'overcast', 'rainy', 'overcast'],
'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}
df = pd.DataFrame(dataset_dict)
# 准备模型数据
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)
# 将数据分为训练集和测试集
X, y = df.drop(columns='Play'), df['Play']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# 缩放数值特征(用于自动二值化)
scaler = StandardScaler()
float_cols = X_train.select_dtypes(include=['float64']).columns
X_train[float_cols] = scaler.fit_transform(X_train[float_cols])
X_test[float_cols] = scaler.transform(X_test[float_cols])
# 训练模型
nb_clf = BernoulliNB()
nb_clf.fit(X_train, y_train)
# 进行预测
y_pred = nb_clf.predict(X_test)
# 检查准确度
print(f"准确度: {accuracy_score(y_test, y_pred)}")```

























 393
393

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










