深度学习（第2章——卷积和转置卷积）

前言：

        本章介绍了计算机视觉中重要的卷积层原理以及pytorch的底层实现，以及超分辨率中常用的转置卷积具体含义，同时顺带介绍pytorch中一些常用函数的实际作用。

---

卷积：

卷积即使用卷积核（一个矩阵）使用滑动窗口的方法在特征图上（另外一个矩阵）按位置相乘相加得到一个值作为输出对应位置的值。最后的输出也为一个矩阵。矩阵的大小计算公式如下：

输出特征图尺寸o，i为输入尺寸，p为填充，k为卷积核大小，s为步长。

在引入偏置量后，和多个通道（如rgb三色通道）后，单个卷积核得到的计算值公式如下：

易混淆点：

（1）一个卷积核对于多通道是同时处理同时最后输出为一个值，而非n个输出通道得到n个输出值。单个卷积层最终的输出通道数只和卷积核数目有关，一个卷积核对应一个输出通道。

（2）同一卷积核的每个输入通道对应的参数不同但共享同一偏置。如果有三通道输入，且卷积核大小为3则卷积核的参数量应该为3（通道数）*3（卷积核高）*3（卷积核宽）+1（偏置）。

案例代码：

最终输出为

代码解释：

在定义输入特征图后，定义了一个输入通道为1，输出通道也为1即一个卷积核，卷积核大小为3，步长默认为1，无偏置量的卷积层，设置其卷积核参数，并将结果输出。

由于代码为ai生成所以加了很多不必要的东西，借此机会也介绍下这些函数作用。

（1）unsqueeze

unsqueeze函数作用为在指定维度上插入维度，下面两者表示等价：

此时input的shape为[1,1,4,4]，升高维度的原因为卷积层要求输入为[batch,channel,height,width]的形式。

（2）squeeze

squeeze()无参表示移除所有为1的维度，有参表示移除指定维度如果其为1。卷积层的输入核输出形式一致，去掉为1的批次维度和通道维度。

（3）detach

detach()获取新引用张量，且获取的张量自动梯度为false。

detach设计的知识点比较多，这里展开细讲。

1.关于引用

看似此处与detach获取引用的结果冲突，实际问题出现在c = c + 1这行。

pytorch的向量实际相当于是定义了新的类，并对运算符进行了重载。

非原地操作：

这些都会生成一个新的实例，而非在原有向量上更改。

原地操作：

这些则会直接在原有向量上更改

都输出：

而赋值操作则相当于传引用对象，即两个标识符指向同一内存地址。（java对象或c++指针）

2.关于backword:

在理解获取的张量自动梯度为false意义前需要了解backword的实际作用。

backword本质是反向传播+梯度累加，y.backward()会增加参与y计算所有requires_grad=True的向量的梯度而非覆盖。

3.关于梯度截断：

通过上述代码能够画出一个计算图。

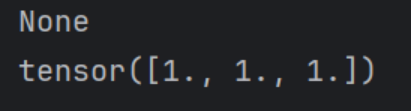
在上一章我们知道由于链式法则，pytorch计算图中每个节点的梯度计算都依赖于后一个结点的梯度.梯度反向传播如果遇到自动梯度为false则梯度不会再被该节点传播回去。上述代码显示设置b的自动梯度为false进而导致a的梯度为none。

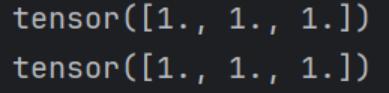
设置为true后结果如下：

4.实质

detach() 的实质是创建一个与原张量共享数据内存（storage）的新张量，但会断开它与计算图的连接（即禁用梯度追踪）。（在Gan网络训练中会经常看到将生成器生成的特征图进行detach防止判别器对特征图操作导致生成器的梯度受到影响。）

感受野：

感受野大小等于经过这层得到的特征图上一个像素对应原图的像素大小。可以通过递归的公式计算：

案例如下：

感受野小更关心局部特征如纹理，感受野大能获取更大范围的语义信息。使用不同大小感受野的卷积搭配能够完成不同类型的任务。

---

转置卷积：

卷积的作用是压缩特征图，将n个输入值对应1个输出值，负责提取高频信息，可以帮助识别等任务，而转置卷积则可视为卷积的逆过程，将1个输入映射出多个数据。可以完成超分辨率等任务。

其计算可理解如下，当步长为1时，对于输入矩阵的每一个值均乘卷积核得到新的矩阵放到结果的对应位置，如果之前对应位置有值则进行累加。

下面为示例代码：

输出：

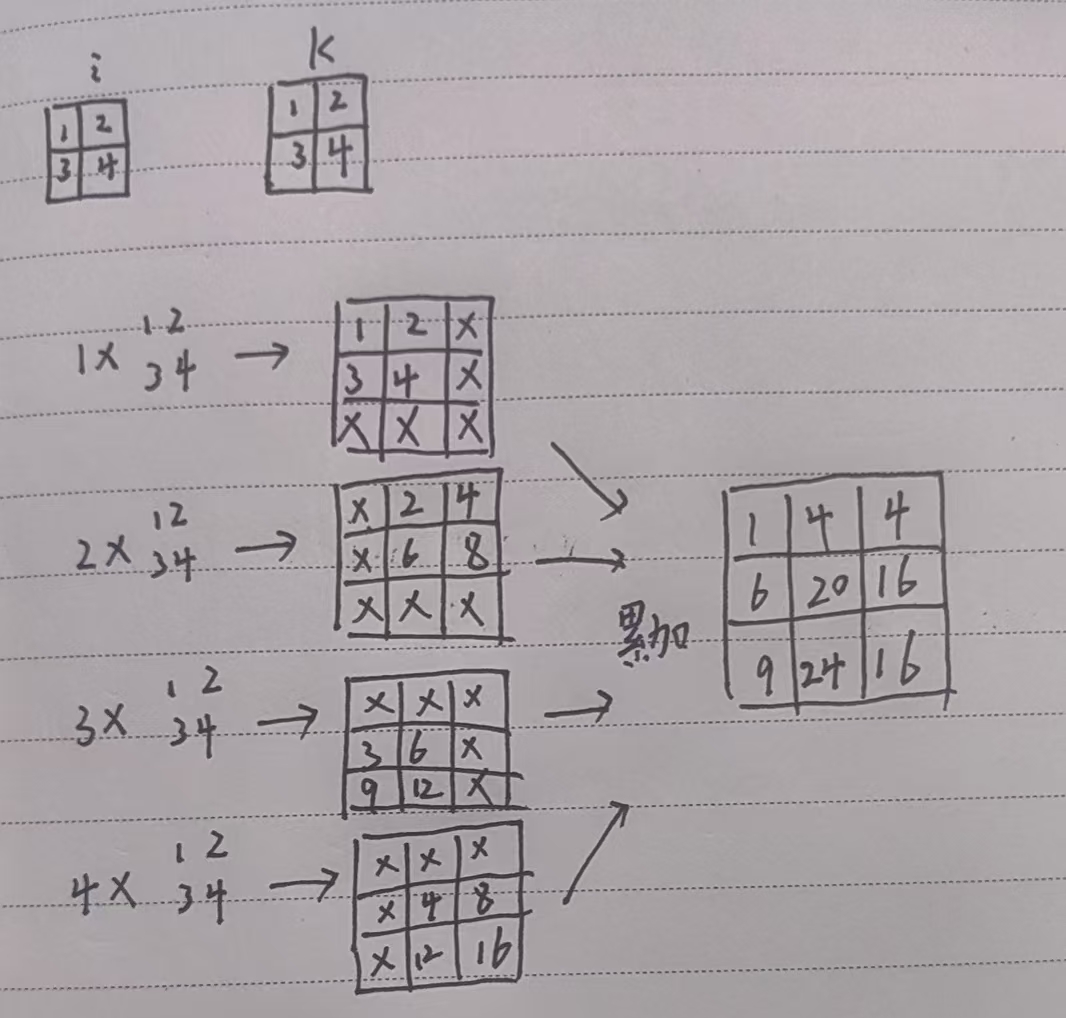
设置padding为1，则表示将四周一圈去掉宽度为1的值

设置padding为2，由于最终输出总共就为3*3,所以会报错

步长表示在原有输入值中间填充几个0，将原图扩充为稀疏矩阵后再进行上述操作，直接与最后输出尺寸相关。

输入输出尺寸关系如下：

（s为步长，k为卷积核大小）

---

最后：

关于转置卷积很多博客都有这两张图，第一张图相当于把卷积核的滑动操作转化为用一整个矩阵一次相乘直接获得。第二张图则将这个卷积矩阵转置乘原本的输出以还原最开始的输入，但需要明确知道除非是正交矩阵否则矩阵的转置不等于逆矩阵，所以上述转置只是单纯还原了尺寸而非数据，以及卷积层和转置矩阵层的卷积核参数是相互独立的，个人感觉通过滑动窗口的方式比直接看两个矩阵更为直接所以就没放在正文。