四、规则化和不可分处理
我们一直假设数据是可分的,不论是引入核函数前的线性可分SVM,还是利用核函数处理非线性数据,都是在可分的情况下。如果不是因为数据本身的非线性结构而是由噪声数据引起的偏离要怎么处理呢?怎么才能在不可分的情况下找到分割超平面呢?
首先我们先看一下为什么离群点会对超平面造成很大的影响(个人感觉算是SVM的一个缺点)。假设下面这样一幅图(来自这里)。

被圈起来的蓝色的点就是一个离群点,本来如果没有它,就可以用红线作为超平面效果看上去不错,但是正因为有了这个点,超平面不得不平移到黑色虚线处。这还是比较好的情况,如果这个点跑到了粉色点的区域,那么连超平面都找不到了。解决这个问题的方法就是加入约束条件构造软间隔SVM。
约束条件改为:

其中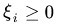 称之为松弛变量,对应于数据点i可以偏离函数间隔的程度,允许某些样本点的函数间隔小于1,最极端的情况是函数间隔变成了负数,即样本点跑到了对方的区域中。但是如果不对松弛变量进行控制的话,松弛变量无限大,那么所有的超平面都符合条件了。所以我们也对目标函数进行了限制,变成
称之为松弛变量,对应于数据点i可以偏离函数间隔的程度,允许某些样本点的函数间隔小于1,最极端的情况是函数间隔变成了负数,即样本点跑到了对方的区域中。但是如果不对松弛变量进行控制的话,松弛变量无限大,那么所有的超平面都符合条件了。所以我们也对目标函数进行了限制,变成
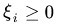 称之为松弛变量,对应于数据点i可以偏离函数间隔的程度,允许某些样本点的函数间隔小于1,最极端的情况是函数间隔变成了负数,即样本点跑到了对方的区域中。但是如果不对松弛变量进行控制的话,松弛变量无限大,那么所有的超平面都符合条件了。所以我们也对目标函数进行了限制,变成
称之为松弛变量,对应于数据点i可以偏离函数间隔的程度,允许某些样本点的函数间隔小于1,最极端的情况是函数间隔变成了负数,即样本点跑到了对方的区域中。但是如果不对松弛变量进行控制的话,松弛变量无限大,那么所有的超平面都符合条件了。所以我们也对目标函数进行了限制,变成
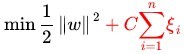
因为如果离群点越多,目标函数值越大,我们要尽可能小的目标函数值,C是离群点的权重,C越大表示离群点对目标函数的影响越大,越不希望看到离群点。所以新的模型变为
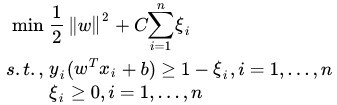
还是构建拉格朗日函数:
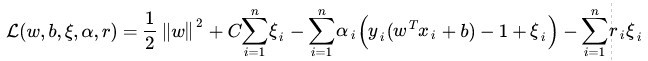
和以前一样,转换为对偶问题之后先对w、b和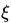 (需要最优化的参数)进行最小化操作
(需要最优化的参数)进行最小化操作
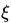 (需要最优化的参数)进行最小化操作
(需要最优化的参数)进行最小化操作
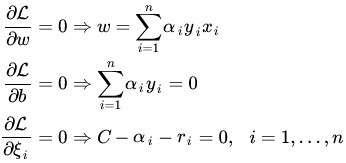
带回w,发现其实目标函数和以前一样,只不过约束条件变了
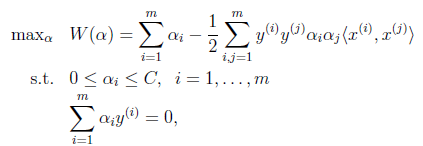
其实隐含的东西还有:b的求解方法变了,KKT条件变了。
KKT条件变为:
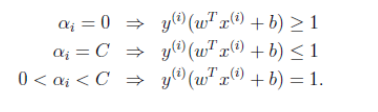
第一个式子表明在两条间隔线外的样本点前面的系数为0,离群样本点前面的系数为C,而支持向量(也就是在超平面两边的最大间隔线上)的样本点前面系数在(0,C)上。
之所以这样是因为对于离群点来说(1)在两个超平面之间wx+b|<1,y=-1或1,因此公式成立。(2)在对方的超平面内或者对方的超平面上虽然wx+b>=1,但y=-1或者wx+b<=-1,y=1。因此y(wx+b)<1。(3)在自己类的超平面上时
等号
可能成立。
总结一下:
解决线性不可分的情况下用核函数,可以将维度映射到高维空间上。对于有噪声等产生了离群点的时候,用规则化方式解决不可分问题。至于参数C的选择、核函数的选择则需要根据实际情况选择。可以用列举的方式观察最佳参数。
























 2857
2857

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








