注:该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。
指数-三角优化(Exponential-trigonometric optimization, ETO)是一种新颖强大的优化器,它基于指数函数和三角函数的复杂组合。ETO算法的结构是为了在两个重要阶段之间取得平衡:勘探和开发,这是许多其他优化算法也试图解决的挑战。与现有算法相比,ETO使用指数函数和三角函数来调整代理的位置,有效地实现了平衡。ETO建立在指数函数和三角函数的结合上。结构设计简单,实现方便,优化时参数调整方便。这不仅提高了算法在探索和利用搜索空间方面的性能,而且为许多不同类型的问题提供了灵活性和适应性。该成果于2024年发表在工程技术领域1区SCI期刊“Computer Methods in Applied Mechanics and Engineering”上。

1.算法原理
(1)约束勘探法
搜索空间在优化算法中起着至关重要的作用。利用和明确定义搜索空间对最终结果有很大的影响。这是因为在大空间中搜索会消耗大量的时间和计算资源,而在太窄的空间中搜索可能会错过最优解。
一些研究提出了约束搜索策略,以最大限度地利用潜在空间并提高性能。这种策略有助于限制搜索空间,减少所需的时间和计算资源,同时仍然确保不会错过最优解决方案。具体来说,在ETO算法中,提出了一种有限探索方法。该方法通过使用以下公式便于高效地探索和利用搜索空间。这有助于优化搜索过程,减少所需的时间和计算资源,同时确保不遗漏最优解:
式中,t表示当前迭代次数,Max_Iter对应总迭代次数,floor为MATLAB中执行舍入运算的函数,a和b为两个调整系数,分别取4.6和1.55。CEi的值由下式确定,而CEi+1表示启动当前和后续约束探索方法的迭代计数。
采用约束搜索策略后,该方法同时更新搜索空间的上限和下限。这个更新过程是策略的一个组成部分,确保搜索空间是动态适应的,以提高优化过程的效率。上限和下限的调整由以下公式控制:
其中,Upi和Lowi分别表示预期搜索空间的上限和下限。R1和r2是在0和1之间随机取的两个系数。 表示到目前为止得到的最优解的第j个位置。 表示次优解在第j个指标处的位置。
(2)初始化阶段
ETO通过随机产生潜在种群的集合来启动其过程。在这种情况下,N表示总体 ,其中 , ,并且该种群中的每个个体都由其在d维中的位置定义。如下式所示,ETO内的种群可以使用特定的矩阵表示来表示:

随机初始化的公式可以用如下方式描述:
其中rand()表示区间[0,1]内的随机值。第j维以Upj和Lowj为界,分别表示上限和下限, 和 。
(3)探索方法
在本研究中,下一个位置的确定不仅受到当前位置的影响,还受到迄今为止确定的最佳解决方案的影响。在优化过程中,探索阶段分为两个阶段,在随后的迭代中维持这一阶段以防止收敛到局部最优点是至关重要的。这两个阶段之间的过渡由下式控制。
(4)第一个探索阶段
在优化过程的早期阶段,初始化种群并确定搜索空间的边界后,个体开始对搜索域进行探索。在第一步,他们在这个巨大的搜索空间中探索潜在的位置。然后,在接下来的一组步骤中,这些个体将逐渐移动到找到的最佳位置。在这个初始探索阶段,根据下式来更新个体的位置:
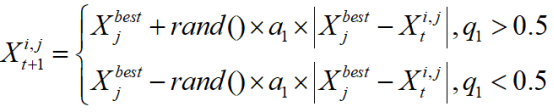
在这种情况下,到该点为止发现的最优解的第j个位置用 表示。 和 分别用于表示当前迭代和后续迭代中第i个解的第j个位置。t是当前迭代的标记。随机数[0,1]区间用q1和rand()表示。在第一阶段, 的权重系数为α1。候选解的初始阶段受α1权值的控制,使得候选解逐渐从自身向最佳解探索。该值由下式确定。
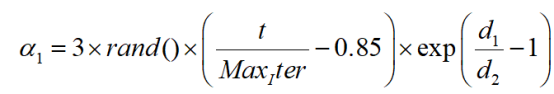
此外,下图说明了α1在整个初始轮中如何显著变化。然而,在随后的重复实验中,α1值逐渐趋于稳定,振荡幅度逐渐减小。这说明了系数如何帮助算法逐渐收敛并随后寻找更理想的值。
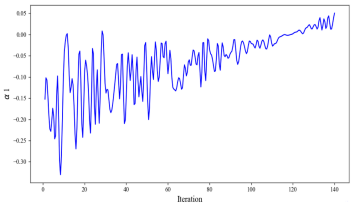
(5)第二个开发阶段
在开发的后期阶段,候选解决方案将围绕到那时为止已确定的最优解决方案进行更深入的探索。这一阶段的特点是在最优解附近进行深入而集中的探索。随着迭代的进行,这种局部探索的强度增加,表明越来越重视最优解。这种在搜索空间的最有利区域内加强搜索的策略由下式控制,它为更新候选解的位置提供了数学框架:
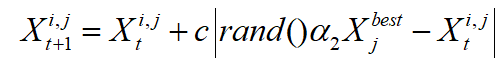
在此上下文中,rand()表示落在[0,1]区间内的随机数。由公式计算得到的权重系数α2在后续开采阶段起着举足轻重的作用。绝对值之前的系数c有助于保持候选解之间的多样性。系数c将根据下式计算:
其中d1和d2由等式(10)、(11)确定。系数c是通过指数函数和三角函数的巧妙结合来确定的,创造了一个独特而有效的机制。这不仅增强了更新最优位置的能力,还优化了搜索过程,提高了性能,并确保找到的解决方案将实现最佳优化。
(6)转换机制
为了能够在勘探和开发阶段之间灵活地移动,需要一种有效的转换技术。在前人研究的基础上,提出了一种新的转换机制来匹配和优化ETO算法的效率。在第一阶段,这种转移机制以勘探为主,但也有少量的开采。随着过程的迭代,这种过渡机制逐渐转向主要关注开发,但仍然保持少量的探索。这种转换机制是根据下式实现的,它有助于确保对完整搜索域的探索和利用,同时在后续迭代中避免局部最优。这创造了一种灵活有效的搜索优化方法:
其中值d1和d2是通过公式计算的。同时,rand()表示从[0,1]范围内选择的随机数。当CM > = 1时,ETO处于勘探模式。反之,当CM < 1时,ETO转为开发模式。
综上所述,ETO算法分为四个主要部分。其中包括边界搜索策略、探索和开发的双重阶段以及CM转换机制。
首先,ETO通过随机生成一组可能的解决方案开始,然后开始对搜索域进行探索。在这一阶段,为了保持搜索空间的可调性,提高优化过程的效率,对上界和下界进行了修正。这包括引导搜索代理向从一定距离获得的最佳解决方案,或利用搜索代理附近的搜索空间。如果没有,ETO将过渡到第二阶段并进行探索,深入研究搜索域的潜在领域。此外,ETO采用边界搜索方法在预期区域内重新分配所有搜索代理,随后进行第二阶段的勘探和开发。在勘探开发过程中,标量参数d1和d2至关重要。d1和d2两个参数,有助于缩小搜索空间,在优化过程中提高收敛速度和准确性。最后,部署过渡过程,在勘探和开采之间交替进行。在探索机制和开发机制之间,这种切换机制有助于确保和灵活地移动。在接下来的迭代中,它还有助于摆脱局部最优。
所提出的ETO伪代码在算法1、2、3、4中进行了详细阐述




ETO的流程图如下所示。
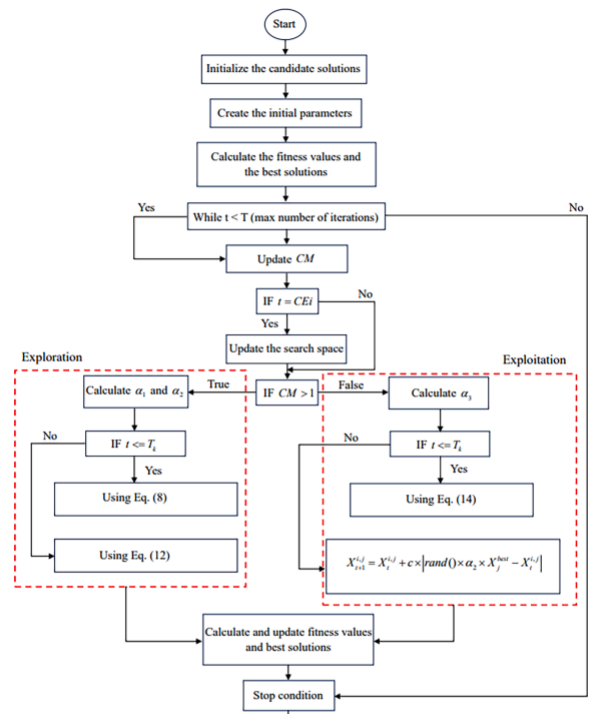
2.结果展示
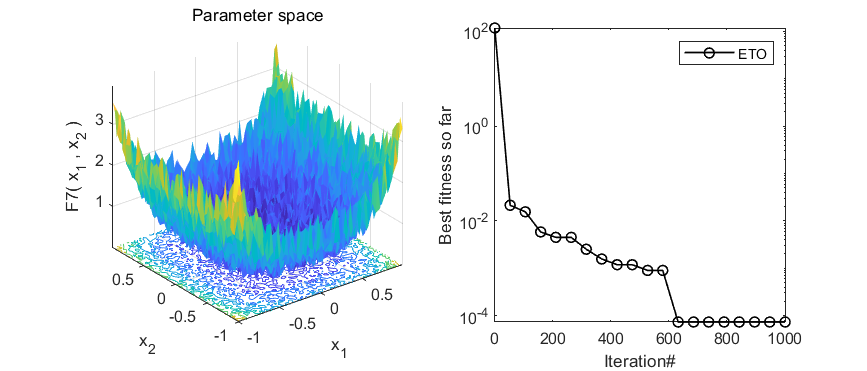
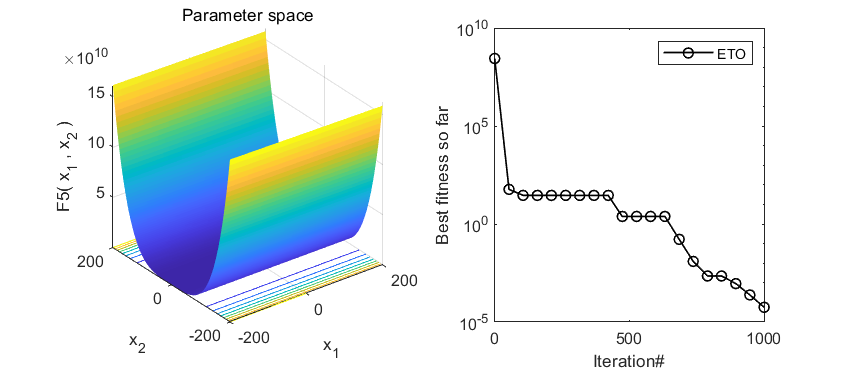
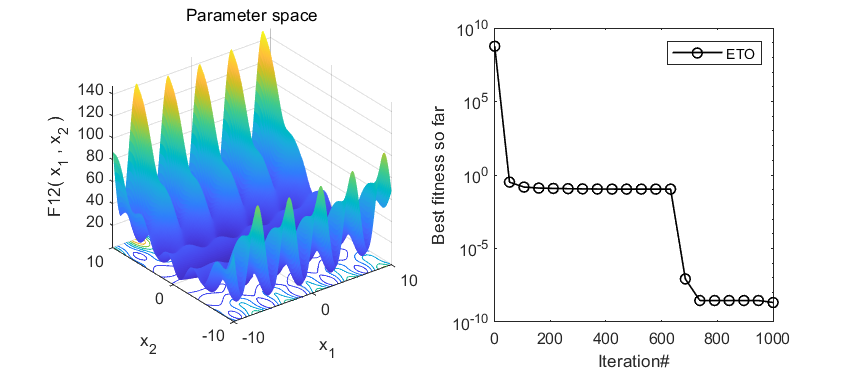
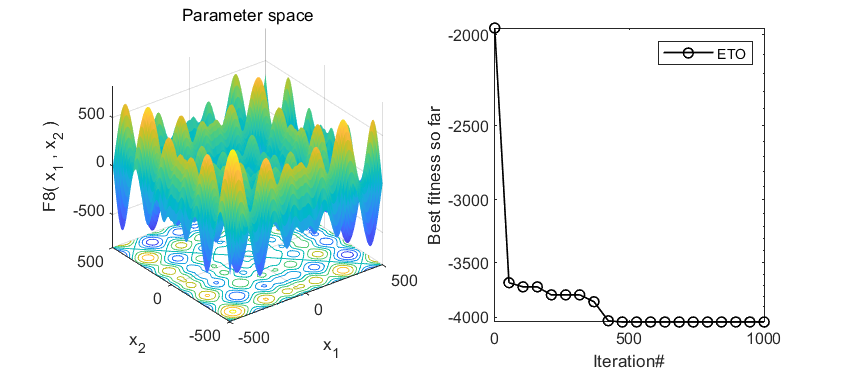
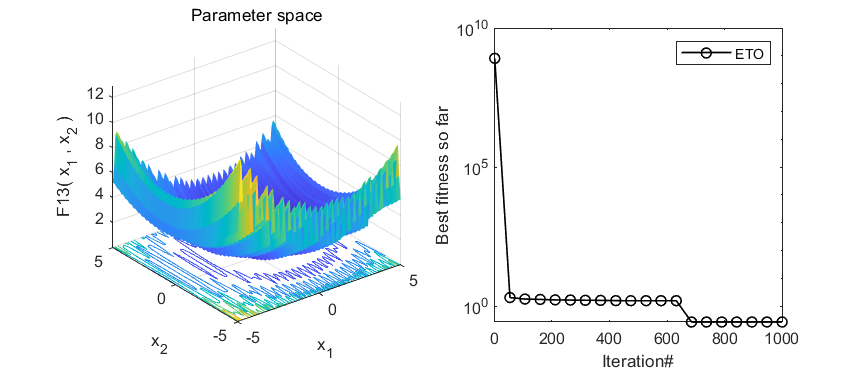
3.MATLAB核心代码
%微信公众号搜索:淘个代码,获取更多免费代码
function [Destination_fitness,Destination_position,Convergence_curve]=ETO(N,Max_Iter,LB,UB,Dim,Fobj)
% N-种群数,Max_It-最大迭代次数,LB-下限,UB-上限,Dim-维度,Fobj-目标函数
Destination_position=zeros(1,Dim);
Destination_fitness=inf;
Destination_position_second=zeros(1,Dim);
Convergence_curve=zeros(1,Max_Iter);
Position_sort = zeros(N,Dim);
%Initialize ETO parameters
b=1.55;
CE=floor(1+(Max_Iter/b));
T=floor(1.2+Max_Iter/2.25);
CEi=0;
CEi_temp=0;
UB_2=UB;
LB_2=LB;
%Initialize the set of random solutions
X=initialization(N,Dim,UB,LB);
Objective_values = zeros(1,size(X,1));
% Calculate the fitness of the first set and find the best one
for i=1:size(X,1)
Objective_values(1,i)=Fobj(X(i,:));
if Objective_values(1,i)<Destination_fitness
Destination_position=X(i,:);
Destination_fitness=Objective_values(1,i);
end
end
Convergence_curve(1)=Destination_fitness;
t=2;
%Main loop
while t<=Max_Iter
for i=1:size(X,1) % in i-th solution
for j=1:size(X,2) % in j-th dimension
%update A by using Eq. (17)
d1=0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (1 - t / Max_Iter));
d2=-0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (1 - t / Max_Iter));
CM=(sqrt(t/Max_Iter)^tan(d1/(d2)))*rand()*0.01;
% enter the bounded search strategy
if t==CEi
UB_2=Destination_position(j)+(1-t/Max_Iter)*abs(rand()*Destination_position(j)-Destination_position_second(j))*rand();
LB_2=Destination_position(j)-(1-t/Max_Iter)*abs(rand()*Destination_position(j)-Destination_position_second(j))*rand();
if UB_2>UB
UB_2=UB;
end
if LB_2<LB
LB_2=LB;
end
X=initialization(N,Dim,UB_2,LB_2);
CEi_temp=CEi;
CEi=0;
end
% the first phase of exploration and exploitation
if t<=T%3.6-3.62
q1=rand();
q3=rand();
q4=rand();
if CM>1
d1=0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (q1));
d2=-0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (q1));
alpha_1=rand()*3*(t/Max_Iter-0.85)*exp(abs(d1/d2)-1);
if q1<=0.5
X(i,j)=Destination_position(j)+rand()*alpha_1*abs(Destination_position(j)-X(i,j));
else
X(i,j)=Destination_position(j)-rand()*alpha_1*abs(Destination_position(j)-X(i,j));
end
else
d1=0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (q3));
d2=-0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (q3));
alpha_3=rand()*3*(t/Max_Iter-0.85)*exp(abs(d1/d2)-1.3);
if q3<=0.5
X(i,j)=Destination_position(j)+q4*alpha_3*abs(rand()*Destination_position(j)-X(i,j));
else
X(i,j)=Destination_position(j)-q4*alpha_3*abs(rand()*Destination_position(j)-X(i,j));
end
end
else
% the second phase of exploration and exploitation
q2=rand();
alpha_2=rand()*exp(tanh(1.5*(-t/Max_Iter-0.75) - rand()));
if CM<1
d1=0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (q2));
d2=-0.1*exp(-0.01 * t) * cos(0.5 * Max_Iter * (q2));
X(i,j)= X(i,j)+exp(tan(abs(d1/d2))*abs(rand()*alpha_2*Destination_position(j)-X(i,j)));
else
if q2<=0.5
X(i,j)=X(i,j)+3*(abs(rand()*alpha_2*Destination_position(j)-X(i,j)));
else
X(i,j)=X(i,j)-3*(abs(rand()*alpha_2*Destination_position(j)-X(i,j)));
end
end
end
end
CEi=CEi_temp;
end
for i=1:size(X,1)
% Check if solutions go outside the search spaceand bring them back
Flag4ub=X(i,:)>UB_2;
Flag4lb=X(i,:)<LB_2;
X(i,:)=(X(i,:).*(~(Flag4ub+Flag4lb)))+(UB_2+LB_2)/2.*Flag4ub+LB_2.*Flag4lb;
% Calculate the objective values
Objective_values(1,i)=Fobj(X(i,:));
% % Update the destination if there is a better solution
if Objective_values(1,i)<Destination_fitness
Destination_position=X(i,:);
Destination_fitness=Objective_values(1,i);
end
end
% find the second solution
if t==CE
CEi=CE+1;
CE=CE+floor(2-t*2/(Max_Iter-CE*4.6)/1);
temp = zeros(1,Dim);
temp2 = zeros(N,Dim);
%sorting
for i=1:(size(X,1)-1)
for j=1:(size(X,1)-1-i)
if Objective_values(1,j) > Objective_values(1,j+1)
temp(1,j) = Objective_values(1,j);
Objective_values(1,j) = Objective_values(1,j+1);
Objective_values(1,j+1) = temp(1,j);
temp2(j,:) = Position_sort(j,:);
Position_sort(j,:) = Position_sort(j+1,:);
Position_sort(j+1,:) = temp2(j,:);
end
end
end
Destination_position_second=Position_sort(2,:);%the second solution
end
Convergence_curve(t)=Destination_fitness;
t=t+1;
end4.参考文献
[1]Luan T M, Khatir S, Tran M T, et al. Exponential-trigonometric optimization algorithm for solving complicated engineering problems[J]. Computer Methods in Applied Mechanics and Engineering, 2024, 432: 117411.
下方卡片获取代码
























 822
822

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










