差分变异的松鼠搜索算法，MATLAB代码免费获取

差分松鼠搜索算法（A Differential Squirrel Search Algorithm，DSSA）是混合式的智能优化算法。该算法将松鼠搜索算法的搜索方法与差分进化优化过程相结合，充分利用了两者优越性。其中松鼠搜索算法是一种受自然启发的群智能优化算法，其灵感来源于松鼠这种动物的生存策略；差分算法的交叉特性增强了松鼠在觅食过程中的探索能力，从而减少了陷入局部极小值的机会。此外，在每次迭代中对松鼠位置的更新规则进行了修改，使松鼠在冬季到来之前在更短的时间内到达最佳食物源。

该组合式的优化算法具有进化能力强、搜索速度快、寻优能力强的特点。该成果是2021年发表的。

DSSA通过结合差分进化算法（DE）和松鼠搜索算法（SSA）。在SSA中，松鼠通过跟随松鼠在山核桃树或橡子树中的位置来更新它们的位置。因此，这些领先松鼠的更新规则已被修改，以改善其搜索策略。通过引入受DE启发的交叉操作，进一步提高了算法的探测能力。DSSA中包含的不同觅食策略是数学建模的。

1、算法原理

（1）随机初始化

森林中有n只松鼠，第i只松鼠的位置可以用一个向量来表示。所有松鼠的位置可以用下面的矩阵表示：

其中FSi,j表示第i只松鼠的第j维。下式用于分配森林中每只松鼠的初始位置。

其中FSL和FSU分别是第i只松鼠在第j维上的下界和上界，U（0，1）是范围[0，1]内的均匀分布随机数。

（2）初始位置更新

在没有捕食者的情况下，橡子树上的松鼠会更新自己的位置，并通过跟随当前最佳的PSht向最佳来源移动。普通树中的松鼠通过跟随橡子树或山核桃树中的松鼠来更新其位置。松鼠在捕食者面前觅食时会随机改变路径。

橡子树上的松鼠现在根据其他松鼠的位置更新自己的位置，如式所示:

其中Pavg是当前种群中所有松鼠的平均位置。

（3）差分进化算法交叉操作 此外，为了避免陷入局部极小值的可能性，还利用差分进化算法的交叉机制增加了松鼠的多样性。对松鼠的当前位置和分别由下式得到的新位置进行交叉操作：

其中i=1,2,3,....NP，NP是总体大小。 是是交叉操作后松鼠的位置。 和 是目前松鼠在橡子树新的和旧的位置。D是问题的维数，Cr是取为0.5的交叉率。 是随机生成的索引。 表示在给定范围内均匀生成的随机数的第j次评估。

出现在正常树上的一些松鼠会跟随松鼠在橡子树上的位置移动到新的位置：

式中r2为均匀分布在[0,1]范围内的随机数。

其余的松鼠在正常的树上跟随当前的最佳位置，它们的新位置表示为:

对正常树内的松鼠进行交叉操作，具体操作如下:

对正常树内的松鼠进行交叉操作，具体操作如下:

通过允许山核桃树中的松鼠根据山核桃树中松鼠位置的平均值更新其位置，进一步提高了收敛速度:

其中 是橡子树上所有松鼠位置的平均值。

然后在选择过程中将新位置及其交叉位置中的最佳位置与旧位置进行比较，以参加下一代种群。DSSA的具体步骤见算法1

2、结果展示

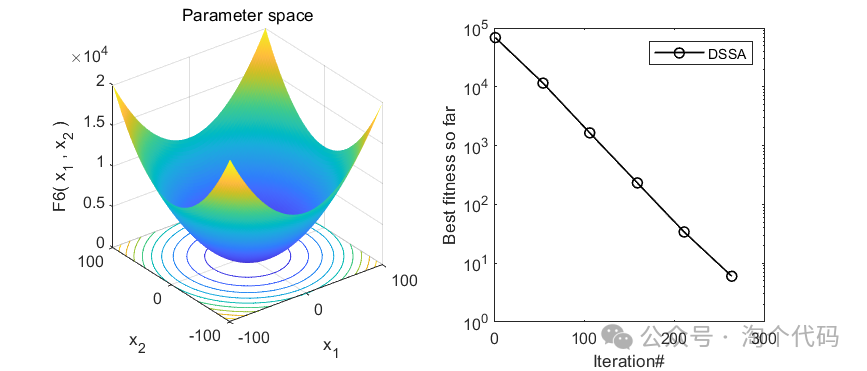
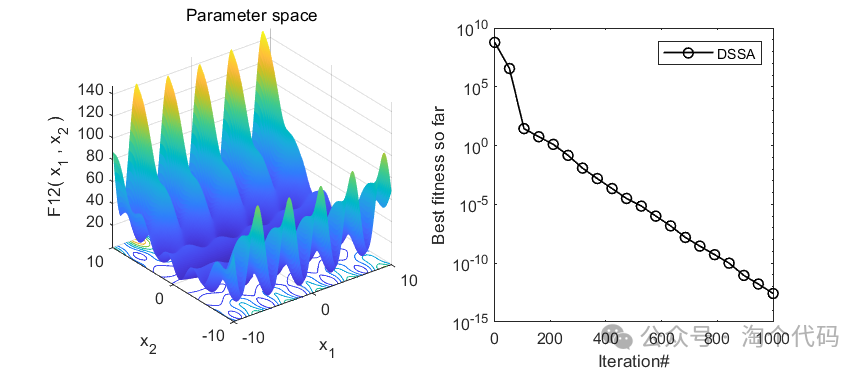
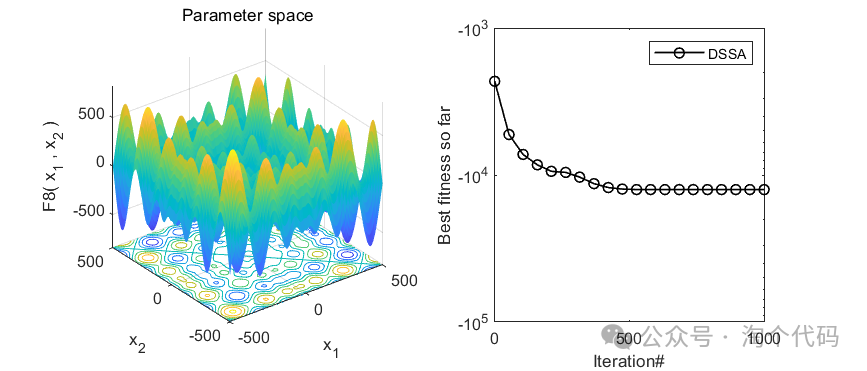
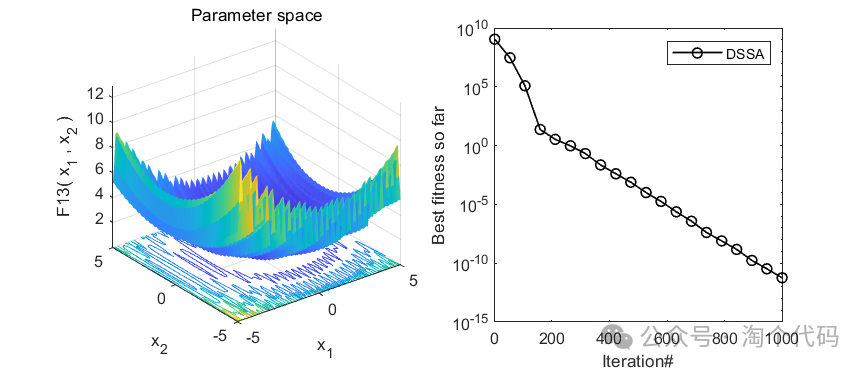
以上4个函数是CEC2005中较难的几个函数。可以看到，均未陷入局部最优，证明该算法还不错！大家可以借鉴该算法，去改进一些别的算法！

3.MATLAB代码展示

%%
function [best_fitness,best_solution,curve] = dssa(population_size, max_iterations, lower_bound, upper_bound,num_variables, objective_function)
    F = 0.35; % Differential weight
    CR = 0.08; % Crossover rate
    % Initialization


    population = lower_bound + (upper_bound - lower_bound) * rand(population_size, num_variables); % Initialize population
    fitness = zeros(population_size, 1); % Initialize fitness values
    best_solution = zeros(1, num_variables); % Best solution found so far
    best_fitness = inf; % Best fitness found so far
    
    % Main loop
    for iter = 1:max_iterations
        % Evaluate fitness for each individual in the population
        for i = 1:population_size
            fitness(i) = objective_function(population(i, :));
            
            % Update best solution if the current solution is better
            if fitness(i) < best_fitness
                best_fitness = fitness(i);
                best_solution = population(i, :);
            end
        end
        
        % Generate mutant vectors using differential evolution
        mutant_population = zeros(population_size, num_variables);
        for i = 1:population_size
            % Select three random individuals different from the current one
            indices = randperm(population_size, 3);
            r1 = population(indices(1), :);
            r2 = population(indices(2), :);
            r3 = population(indices(3), :);
            
            % Generate mutant vector using differential mutation
            mutant = r1 + F * (r2 - r3);
            
            % Clip the mutant vector to the bounds
            mutant = min(max(mutant, lower_bound), upper_bound);
            
            mutant_population(i, :) = mutant;
        end
        
        % Crossover operation (binomial crossover)
        trial_population = zeros(population_size, num_variables);
        for i = 1:population_size
            % Randomly select crossover points
            crossover_points = rand(1, num_variables) < CR;
            
            % Perform crossover
            trial_population(i, :) = population(i, :);
            trial_population(i, crossover_points) = mutant_population(i, crossover_points);
        end
        
        % Selection (replace current population with trial population if it's better)
        for i = 1:population_size
            trial_fitness = objective_function(trial_population(i, :));
            
            % Replace current population with trial population if it's better
            if trial_fitness < fitness(i)
                population(i, :) = trial_population(i, :);
                fitness(i) = trial_fitness;
                
                % Update best solution if the trial solution is better
                if trial_fitness < best_fitness
                    best_fitness = trial_fitness;
                    best_solution = trial_population(i, :);
                end
            end
        end


        curve(iter)=best_fitness;
    end
end

3.参考文献

[1]Jena B, Naik M K, Wunnava A, et al. A differential squirrel search algorithm[C]//Advances in Intelligent Computing and Communication: Proceedings of ICAC 2020. Springer Singapore, 2021: 143-152.

完整代码获取