SVM的几点
1.SVM的思想
SVM的思想可以表达为:SVM试图寻找一个超平面来对样本进行分割,把样本中的正例和反例用超平面分开,但是不是很敷衍地简单的分开,而是尽最大的努力使正例和反例之间的间隔最大,即正例和反例的支持向量距离超平面距离最大。如下图
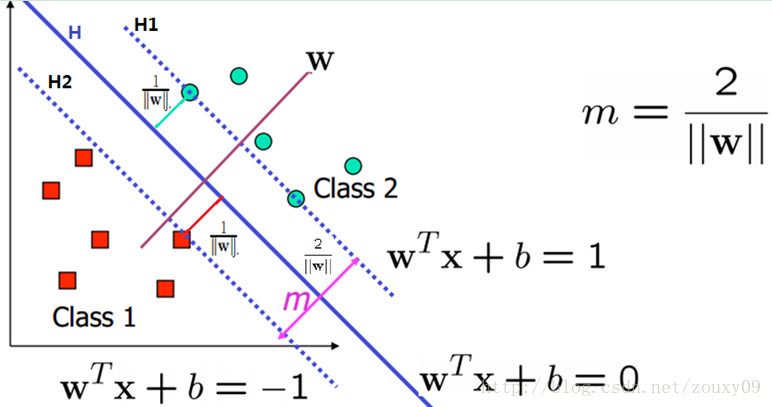
为了最大化这个距离,问题化为:
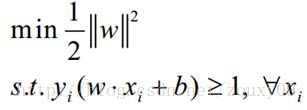
(一)关于拉格朗日乘子法
(二)关于KKT条件
2.SVM优化对偶问题
需要优化的是:
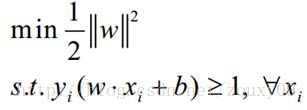
引入拉格朗日乘子,我们就可以得到以下拉格朗日函数:
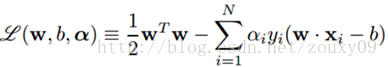
分别对w和b进行求偏导,得到:
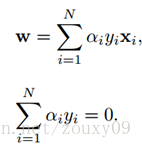
再代入拉格朗日函数:
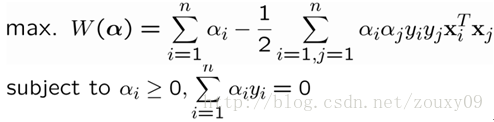
最后得到分离超平面和分类决策函数
3.加入松弛变量
示例:
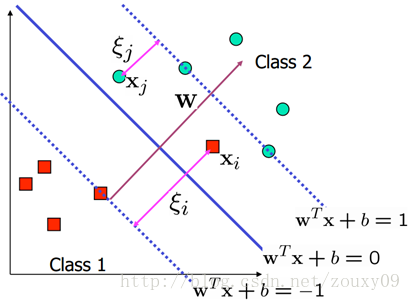
约束条件为:
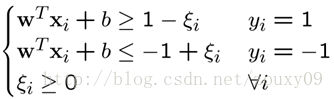
在目标函数里面增加一个惩罚项,新的模型就变成为:
引入拉格朗日乘子并分别求导:
带松弛变量的优化函数以及约束条件为:
4.核函数
著名的cover定理:将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。
可以把的原始样本点通过一个变换,变换到另一个特征空间,在这个特征空间上是线性可分的,那么SVM就可以工作。也就是说,对于不可分的数据,现在要做两个工作:
1)首先使用一个非线性映射Φ(x)将全部原始数据x变换到另一个特征空间,在这个空间中,样本变得线性可分了;
2)然后在特征空间中使用SVM进行学习分类。
常用的核函数为高斯核函数:
5.SMO算法
大致步骤:
优化目标,并且满足KKT条件:
并且满足条件:
得到α1和α2的关系:
根据上面的α2的范围,求解它的值,证明为:
计算出α1:
由α1和α2计算出 w 和 b :
Python实现SVM
import numpy as np
from numpy import linalg
import cvxopt
import cvxopt.solvers
def linear_kernel(x1, x2):
return np.dot(x1, x2) # 矩阵乘法
def polynomial_kernel(x, y, p=3):
return (1 + np.dot(x, y)) ** p
def gaussian_kernel(x, y, sigma=5.0):
return np.exp(-linalg.norm(x-y)**2 / (2 * (sigma ** 2)))
class SVM(object):
def __init__(self, kernel=linear_kernel, C=None):
self.kernel = kernel
self.C = C
if self.C is not None: self.C = float(self.C)
def fit(self, X, y):
n_samples, n_features = X.shape
# Gram matrix
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
for j in range(n_samples):
K[i,j] = self.kernel(X[i], X[j])
P = cvxopt.matrix(np.outer(y,y) * K)
q = cvxopt.matrix(np.ones(n_samples) * -1)
A = cvxopt.matrix(y, (1,n_samples))
b = cvxopt.matrix(0.0)
if self.C is None:
G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1))
h = cvxopt.matrix(np.zeros(n_samples))
else:
tmp1 = np.diag(np.ones(n_samples) * -1)
tmp2 = np.identity(n_samples)
G = cvxopt.matrix(np.vstack((tmp1, tmp2)))
tmp1 = np.zeros(n_samples)
tmp2 = np.ones(n_samples) * self.C
h = cvxopt.matrix(np.hstack((tmp1, tmp2)))
# solve QP problem
solution = cvxopt.solvers.qp(P, q, G, h, A, b)
# Lagrange multipliers
'''
数组的flatten和ravel方法将数组变为一个一维向量(铺平数组)。
flatten方法总是返回一个拷贝后的副本,
而ravel方法只有当有必要时才返回一个拷贝后的副本(所以该方法要快得多,尤其是在大数组上进行操作时)
'''
a = np.ravel(solution['x'])
# Support vectors have non zero lagrange multipliers
'''
这里a>1e-5就将其视为非零
'''
sv = a > 1e-5 # return a list with bool values
ind = np.arange(len(a))[sv] # sv's index
self.a = a[sv]
self.sv = X[sv] # sv's data
self.sv_y = y[sv] # sv's labels
print("%d support vectors out of %d points" % (len(self.a), n_samples))
# Intercept
'''
这里相当于对所有的支持向量求得的b取平均值
'''
self.b = 0
for n in range(len(self.a)):
self.b += self.sv_y[n]
self.b -= np.sum(self.a * self.sv_y * K[ind[n],sv])
self.b /= len(self.a)
# Weight vector
if self.kernel == linear_kernel:
self.w = np.zeros(n_features)
for n in range(len(self.a)):
# linear_kernel相当于在原空间,故计算w不用映射到feature space
self.w += self.a[n] * self.sv_y[n] * self.sv[n]
else:
self.w = None
def project(self, X):
# w有值,即kernel function 是 linear_kernel,直接计算即可
if self.w is not None:
return np.dot(X, self.w) + self.b
# w is None --> 不是linear_kernel,w要重新计算
# 这里没有去计算新的w(非线性情况不用计算w),直接用kernel matrix计算预测结果
else:
y_predict = np.zeros(len(X))
for i in range(len(X)):
s = 0
for a, sv_y, sv in zip(self.a, self.sv_y, self.sv):
s += a * sv_y * self.kernel(X[i], sv)
y_predict[i] = s
return y_predict + self.b
def predict(self, X):
return np.sign(self.project(X))
if __name__ == "__main__":
import pylab as pl
def gen_lin_separable_data():
# generate training data in the 2-d case
mean1 = np.array([0, 2])
mean2 = np.array([2, 0])
cov = np.array([[0.8, 0.6], [0.6, 0.8]])
X1 = np.random.multivariate_normal(mean1, cov, 100)
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 100)
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def gen_non_lin_separable_data():
mean1 = [-1, 2]
mean2 = [1, -1]
mean3 = [4, -4]
mean4 = [-4, 4]
cov = [[1.0,0.8], [0.8, 1.0]]
X1 = np.random.multivariate_normal(mean1, cov, 50)
X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50)))
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 50)
X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50)))
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def gen_lin_separable_overlap_data():
# generate training data in the 2-d case
mean1 = np.array([0, 2])
mean2 = np.array([2, 0])
cov = np.array([[1.5, 1.0], [1.0, 1.5]])
X1 = np.random.multivariate_normal(mean1, cov, 100)
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 100)
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def split_train(X1, y1, X2, y2):
X1_train = X1[:90]
y1_train = y1[:90]
X2_train = X2[:90]
y2_train = y2[:90]
X_train = np.vstack((X1_train, X2_train))
y_train = np.hstack((y1_train, y2_train))
return X_train, y_train
def split_test(X1, y1, X2, y2):
X1_test = X1[90:]
y1_test = y1[90:]
X2_test = X2[90:]
y2_test = y2[90:]
X_test = np.vstack((X1_test, X2_test))
y_test = np.hstack((y1_test, y2_test))
return X_test, y_test
# 仅仅在Linears使用此函数作图,即w存在时
def plot_margin(X1_train, X2_train, clf):
def f(x, w, b, c=0):
# given x, return y such that [x,y] in on the line
# w.x + b = c
return (-w[0] * x - b + c) / w[1]
pl.plot(X1_train[:,0], X1_train[:,1], "ro")
pl.plot(X2_train[:,0], X2_train[:,1], "bo")
pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
# w.x + b = 0
a0 = -4; a1 = f(a0, clf.w, clf.b)
b0 = 4; b1 = f(b0, clf.w, clf.b)
pl.plot([a0,b0], [a1,b1], "k")
# w.x + b = 1
a0 = -4; a1 = f(a0, clf.w, clf.b, 1)
b0 = 4; b1 = f(b0, clf.w, clf.b, 1)
pl.plot([a0,b0], [a1,b1], "k--")
# w.x + b = -1
a0 = -4; a1 = f(a0, clf.w, clf.b, -1)
b0 = 4; b1 = f(b0, clf.w, clf.b, -1)
pl.plot([a0,b0], [a1,b1], "k--")
pl.axis("tight")
pl.show()
def plot_contour(X1_train, X2_train, clf):
# 作training sample数据点的图
pl.plot(X1_train[:,0], X1_train[:,1], "ro")
pl.plot(X2_train[:,0], X2_train[:,1], "bo")
# 做support vectors 的图
pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
X1, X2 = np.meshgrid(np.linspace(-6,6,50), np.linspace(-6,6,50))
X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])
Z = clf.project(X).reshape(X1.shape)
# pl.contour做等值线图
pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')
pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')
pl.axis("tight")
pl.show()
def test_linear():
X1, y1, X2, y2 = gen_lin_separable_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM()
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_margin(X_train[y_train==1], X_train[y_train==-1], clf)
def test_non_linear():
X1, y1, X2, y2 = gen_non_lin_separable_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM(gaussian_kernel)
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)
def test_soft():
X1, y1, X2, y2 = gen_lin_separable_overlap_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM(C=0.1)
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)
# test_soft()
# test_linear()
test_non_linear()
PS(cvxopt安装3步)
1.卸载电脑里原有的numpy
2.下载并安装cvxopt(https://www.lfd.uci.edu/~gohlke/pythonlibs/#cvxopt)
3.下载并安装numpy(https://www.lfd.uci.edu/~gohlke/pythonlibs/#numpy)








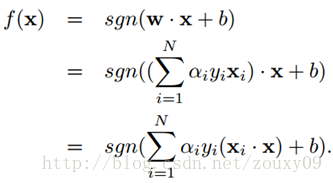














 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








