编辑距离矩阵及在java中的应用

刚好项目有需求要使用到,了解后觉得挺有意思的就发出来跟大家分享下,主要还是为了以后自己可以回头翻翻,大神勿喷啊

下面开始进入正题:

一个原始字符串,经过不断的修改,删除最后变成另外一个字符串,怎么体现出这个字符串的修改痕迹呢,这里面有个最小路径的概念,也就是原始字符串->目标字符串最少要经过多少步骤

假设原字符串:src="abCd";

假设新字符串:dst="ABCD";

那么从abCd->ABCD最少需要经过多少步呢?

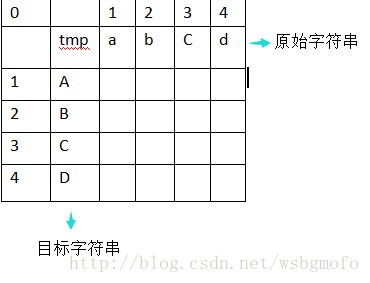
首先,我们先画个矩阵图形来加深理解,如下图

1234表示字符串中每一个字符对应的位置,不一定原始字符串就跟目标字符串一样长,有可能原始字符串比目标字符串长,也可能短,这里为了方便演示就选择了一样长

tmp为中间值,为了后面的计算

然后开始算法,这个算法是哪位数据家提出来的我忘记了,有知道的小伙伴可以留言告知下哈

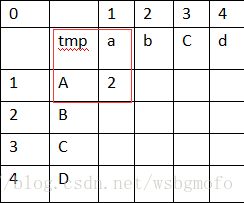
其中有个最小值的概念,以4个小正方形为一组,我们先算出第一个格子的值,如下图

上面红框框出来的小正方形