前段时间研究了non-local算法在双目立体匹配上的应用,这几天又看到作者在PAMI上发表的这篇文章,于是仔细的拜读了一下,惊讶的发现原来NL算法竟然可以应用在多个方向,其实在《A Non-Local Cost Aggregation Method for Stereo Matching》一文中,已经有过关于refinement方面的论述,但是被自己给“忽略”掉了,原来自己的算法知识面还是很窄,汗颜!本文就说一下对于NL在”upsampling”和“refinement”方面的应用的理解。
(转载请注明:http://blog.csdn.net/wsj998689aa/article/details/45584725)
upsampling
upsampling的意思是上采样,是图像方面的概念,之所以要用NL作上采样,主要原因还是速度问题,往往stereo mathcing方向的算法的时间复杂度都比较高,于是为了提高速度,考虑在原图像的下采样图像计算视差图,然后在对低分辨率的视差图进行上采样成为高分辨率的视差图,这是一个折中的方法,效果肯定没有直接在高分辨率图像上生成视差图好,但是速度却能够提高几倍不止。
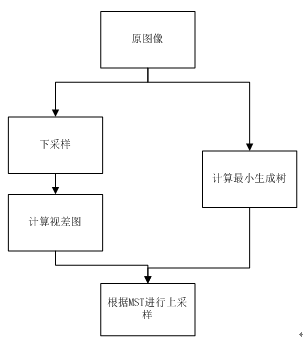
一般的上采样方法相信大家都比较熟悉,最基本的思想就是根据当前像素邻域内的像素值进行估计,比如说权值滤波,也有的文献是基于3Dtof相机获得低分辨率视差图和高分辨率的彩色图,然后在进行上采样操作。这篇文献就是基于权值滤波的思想,将NL应用在了视差图上采样方向,其流程图如下所示:
权重中值滤波公式如下所示:
Note:我认为此处作者的分析存在问题,作者在文章中说:由于可将权重中值滤波等价为代价聚合,进一步可以将上式的绝对值部分视作代价计算项。我认同前一句话,但是不认同后一句话,我们看绝对值中含有自变量b,而代价计算项是不可能含有自变量的,这里严格意义上来说,应该等同于区域内的任意像素与中心像素的比较差值,b和I(q)自身才可被视为代价计算项。不知道有没有童鞋读到这里的时候,和我产生同样的疑问?并且此处作者称之为权重中值滤波,我感觉也说错了,应该是权重均值滤波吧?
由于本文是基于最小生成树的全局算法, 所以N所指的邻域其实包含整幅图像的像素。如此一来,得到的权值更加准确,这也正是NL的优势所在。文献中给出了上采样64倍大小的图像,效果还不错,大家可以去看看。
texture handing
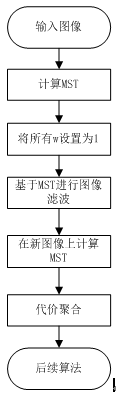
texture handing一般翻译成为纹理抑制或者是纹理处理,指的是对于具有复杂的纹理区域,一般要在边缘保持的同时模糊区域内的纹理,这是一个图像处理上经常用的方法,作者在这上面也下了功夫,目的还是估计视差图,因为NLCA算法对于带噪声图像效果很差,尤其是在其纹理丰富区域,所以催生了这一块应用。我描述了它的算法流程图,如下所示,具体达到的效果大家可以去文献上看看,我就不贴了。
至于如何可以基于MST对纹理进行处理,其实很简单,作者事先检讨了NLCA的不足,他认为距离计算公式(父子节点的像素差值的绝对值)导致了纹理抑制失效,如下图所示,其实我们可以发现,前两幅图基本差不多,差不多就说明了纹理处理没效果。后来他简单的将MST中的距离都设置为1,效果很明显,当然第四幅图由于yita的值设置的过大,抑制的过猛,效果也很差,作者给出了yita的经验值。
但是这样做有个弊端,就是时间复杂度增加了,因为我们为了纹理抑制,要先对图像计算一次MST,只不过将权值设置为1,等代价计算步骤结束之后,还得重新计算一次MST,当然这时是基于纹理抑制之后的图像喽。
refinement
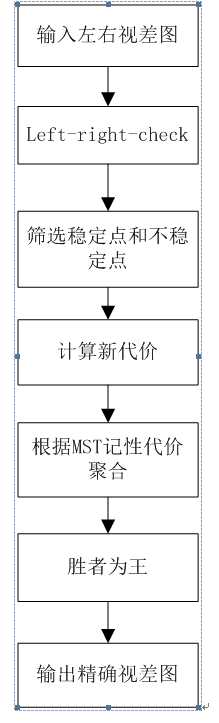
视差图求精是重头戏,由于遮挡,光照等原因,求出来的视差图往往部分点视差不正确,需要对视差图重新求精,是stereo matching必不可少的一步,NL同样在这里有应用,它事先利用left-right-check对左右视差图进行处理,得到视差图的稳定点和不稳定点,同时直接在左视差图上定义新的代价值,再同样利用原图所得的MST,对所有像素点重新进行代价聚合,最后利用”胜者为王”算法估计新的视差。乍一听,感觉这没什么,重点在新的代价值的定义上,公式如下所示:
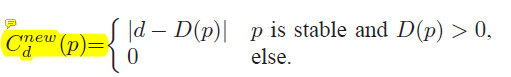
我刚开始看到这个公式,感觉到特别的奇怪,D(p)已经是视差值,它又和视差d相减,这是啥意思?后来明白了作者的意图,这么做其实很直观,就是对旧视差值进行修正,如果旧视差值完全正确,那么计算的将会是d=D(p)。并且,如果p是不稳定点,那么直接赋值为0,注意这只是代价计算的那一步,在后续代价聚合的时候,会重新根据上述公式估计不稳定点的视差。作者称为”利用MST,使得视差值从稳定点扩散至不稳定点”,这是一种很唯美的说法,究其原因,由于不稳定点的代价为0,那么MST上的权值w也就失去了作用,换句话说,不稳定点的代价聚合值完全由稳定点的代价值和权值来累加计算,不能怪人家,谁让你自己不够稳定呢?说白了就是让稳定点更加精确,连带着不稳定点通过MST的计算,也更加精确罢了。
算法流程图如下所示:
代码比较
通过调试作者在网上提供的代码,发现权重中值滤波和求精两个应用其实是完全相同的,返回来再看理论部分,二者采用的公式都完全一样,作者将一个公式应用在了两个方向,并且各自说了一通,成功的屏蔽了俺的双眼,为了予以证明,粘贴作者源码(含有自己的注释)
// upsampling
for(int y=0;y<m_h;y++) for(int x=0;x<m_w;x++)
{
if(disparity[y][x]>0) // 稀疏视差图为0就视为野值
{
for(int d=0;d < m_nr_plane; d++)
{
m_cost_vol[y][x][d]=abs(disparity[y][x]-d);
}
}
} // refinement
for(int y=0;y<m_h;y++) for(int x=0;x<m_w;x++) if(!m_mask_occlusion[y][x]) // 只对稳定点进行处理
{
for(int d=0;d<m_nr_plane;d++)
m_cost_vol[y][x][d]=abs(disparity[y][x]-d);
}大家可以比较一下二者的差异,除了名称不同之外代码基本相同,前者是针对稀疏视差图中视差不为0的像素点,后者针对稳定点,其实都是一样一样的点,再粘贴一下稀疏视差图生成的代码,相信大家一目了然。
// 生成稀疏视差图,注意其与原视差图同样大小
for(int yi=0;yi<(h>>downsample_rate);yi++) for(int xi=0;xi<(w>>downsample_rate);xi++)
{
int y=(yi<<downsample_rate);
int x=(xi<<downsample_rate);
// 由于是视差图下采样,所以必须改变视差,好比一个物体距离你远了,视差自然得变小
disparity[y][x]=(double)disparity_gt[y][x]/scalar;
if(disparity[y][x]<=2)
{
disparity[y][x]=0;
}
}总结
PAMI上的文章有个特点,它的内容往往是很全面的,并且是总结类的文章,就是说作者在之前已经发表过类似的文章,只不过当时只是在某一方面进行了应用,那么在PAMI中往往会添加其他的应用以及完善算法的理论基础,形成一个框架。本文正是如此,如果细看,其实很多内容都与《A Non-Local Cost Aggregation Method for Stereo Matching》一文重复,添加了诸如”texture handling”,”upsampling”,”refinement”方面的应用和解释,再配合以大量的实验,证明这个non-local的idea具有多方面的好处。
特别提的是,本文的序言部分很值得一读,对现有方法总结的很好,希望能够对大家有所帮助。











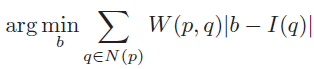



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








