UVA 6910 Cutting Tree 并查集

题目描述：

Tree in graph theory refers to any connected graph (of nodes and edges) which has no simple cycle, while forest corresponds to a collection of one or more trees. In this problem, you are given a forest of N nodes (of rooted trees) and K queries. Each query is in the form of:
• C x : remove the edge connecting node and its parent. If node has no parent, then ignore this query.
• Q a b : output ‘YES’ if there is a path from node to node in the forest; otherwise, ‘NO’.
For example, let the initial forest is shown by Figure 1.

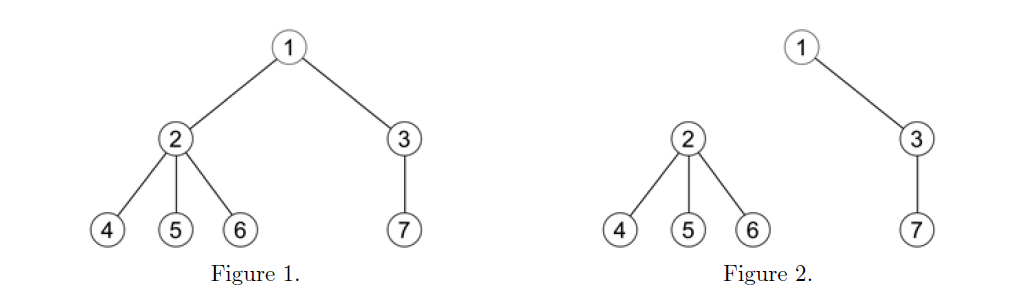
Let’s consider the following queries (in order):
1) Q 5 7 : output YES.
2) C 2 : remove edge (2, 1) — the resulting forest is shown in Figure 2.
3) Q 5 7 : output NO, as there is no path from node 5 to node 7 in Figure 2.
4) Q 4 6 : output YES.
Input
The first line of input contains an integer T (T ≤ 50) denoting the number of cases. Each case begins with two integers: N and K (1 ≤ N ≤ 20, 000; 1 ≤ K ≤ 5, 000) denoting the number of nodes in the
forest and the number of queries respectively. The nodes are numbered from 1 to N. The next line contains N integers Pi (0 ≤ Pi ≤ N) denoting the parent of i-th node respectively. Pi = 0 means that node i does not have any parent (i.e. it’s a root of a tree). You are guaranteed that the given input corresponds to a valid forest. The next K lines represent the queries. Each query is in the form of ‘C x’ or ‘Q a b’ (1 ≤ x, a, b ≤ N), as described in the problem statement above.
Output
For each case, output ‘Case #X:’ in a line, where X is the case number starts from 1. For each ‘Q a b’ query in the input, output either ‘YES’ or ‘NO’ (without quotes) in a line whether there is a path from node a to node b in the forest.
Explanation for 2nd sample case:
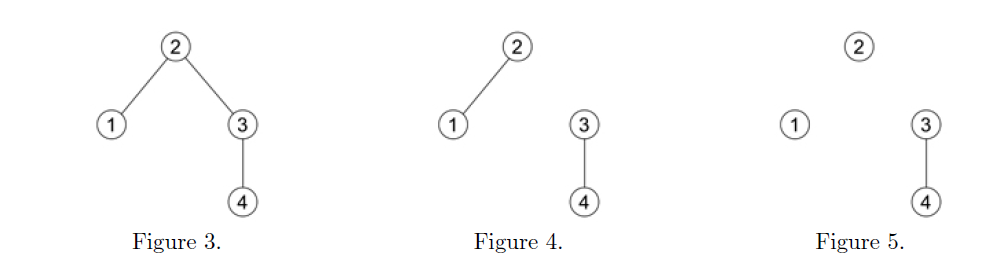
The initial forest is shown in Figure 3 below.
1) C 3 : remove edge (3, 2) — the resulting forest is shown in Figure 4.
2) Q 1 2 : output YES.
3) C 1 : remove edge (1, 2) — the resulting forest is shown in Figure 5.
4) Q 1 2 : output NO as there is no path from node 1 to node 2 in Figure 5.

Sample Input

4
7 4
0 1 1 2 2 2 3
Q 5 7
C 2
Q 5 7
Q 4 6
4 4
2 0 2 3
C 3
Q 1 2
C 1
Q 1 2
3 5
0 3 0
C 1
Q 1 2
C 3
C 1
Q 2 3
1 1
0
Q 1 1

Sample Output

Case #1:
YES
NO
YES
Case #2:
YES
NO
Case #3:
NO
YES
Case #4:
YES

题目分析：

有一棵n个点，m条边的树，给出每个结点的父结点编号，进行操作：
1、C a 将a与其父亲结点连接的边去除
2、Q a b 判断a和b是否能连通 能输出YES不能输出NO

由于这题给的就是每个结点的父结点序号，所以我们不需要建边，其实是一道并查集的变形吧。
刚开始，所有点都在同一个集合中，有共同的祖先结点，也就是那个以自己为根结点的点，每删除一条边，将这个结点的父结点设为自己，也就是多了一个集合，然后用并查集的判断方式看这两点的祖先结点是否相同，就可以判断是否连通（也就是是否在同一棵树上，每一次c操作生成一棵树）

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

const int MAXN=2e5+5;
using namespace std;

int T;
int n,q;
char op[5];
int fa[MAXN];
int a,b;

int find(int u)
{
    if (fa[u]!=u)
    return find(fa[u]);
    else return u;
}

int main()
{
    while(scanf("%d",&T)!=-1)
    {
        for(int t=1; t<=T; t++)
        {
            printf("Case #%d:\n",t);
            scanf("%d%d",&n,&q);
            for(int i=1; i<=n; i++)
            {
                int x;
                scanf("%d",&x);
                if (x!=0) fa[i]=x;
                else fa[i]=i;
            }
            //for(int i=1; i<=n; i++) printf("%d ",fa[i]);
            //printf("\n");
            while(q--)
            {
                cin>>op;
                if (op[0]=='C')
                {
                    scanf("%d",&a);
                    fa[a]=a;
                }
                else
                {
                    scanf("%d %d",&a,&b);
                    if (find(a)==find(b)) printf("YES\n");
                    else printf("NO\n");
                }
            }
        }
    }
    return 0;
}