莱斯利种群算法 python应用

莱斯利种群算法

算法原理

依种群个体的生理特征，将其最大寿命年龄等距分成m个年龄组，然后讨论不同时间种群按年龄的分布，故时间也离散化为

$t=0,1,2,...$其间隔与年龄组的间隔时间相同.$t=0$对应于初始时刻.设开始时$t=0$第i个年龄组内的个体数为

$n_i(0),i=1,2,...,m$则向量$N(0)=[n_1(0),n_2(0),...n_m]$称为初始年龄结构向量.第i年龄组的生殖率为$f_i(>0)i=1,2,...,m$;生存率为$S_i(>0)i=1,2,...,m-1$.则相临两个时段间，各年龄组个体数$n_i$有如下的迭代关系:

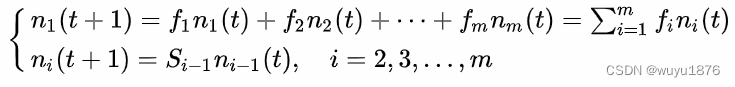
注1 $f_i$中已扣除了在时段t内出生，但活不到$t+1$时段的新生个体.

注2 通常在[两性生殖]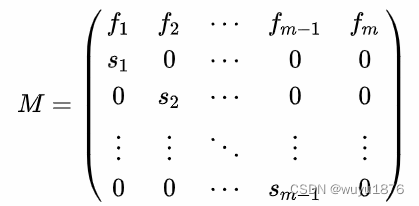

例题

有一块一定面积的草场放牧羊群, 管理者要 估计草场能放牧多少羊, 每年保留多少母羊羔,夏季要 储藏多少草供冬季之用。
为解决这些问题调查了如下的背景资料:
（1）本地环境下这一品种草的日生长率如表 3.5 所列。
表 3.5 各季节草的生长率

季 节	冬	春	夏	秋
日生长率 $/\left(\mathrm{g}/{\mathrm{m}}^2\right)$	0	3	7	4

(2) 羊的繁殖率。通常母羊每年产 $1\sim 3$ 只羊羔, 5 岁后被卖掉。为保持羊群的规模，可以买进羊羔, 或者保留一定数量的母羊。每只母羊的平均繁殖率如表 3.6 所列
表 3.6 母羊的平均繁殖率

年龄	0∼1	1∼2	2∼3	3∼4	4∼5
产羊羔数 只	0	1.8	2.4	2.0	1.8

（3）羊的存活率。不同年龄的母羊的自然存活率（指存活一年）如表3.7所列。

年龄	1~2	2~3	3~4
存活率	0.98	0.95	0.80

（4） 草的需求量。母羊和羊羔得在各个季节每天需要草的数量（kg）

季 节	冬	春	夏	秋
母羊	2.10	2.40	1.15	1.35
羊羔	0	1.00	1.65	0

注：只关心羊的数量，而不管他们的重量，一般在春季产羊高，秋季将全部公羊和一部分母羊卖掉，保持羊群数量

面积为n.

解 用 $\mathbf{x}={\left[x_1,x_2,x_3,x_4,x_5\right]}^{\mathrm{T}}$ 表示母羊按年龄 $0\sim 1,1\sim 2,2\sim 3,3\sim 4,4\sim 5$ 的概率分布 向量, 这里 $x_i⩾0,{\sum }_{i=1}^5{x}_i=1$, 由母羊的繁殖率和存活率可得种群数量的转移矩阵为
$$\mathbf{P}=\left[\begin{array}{ccccc}0& 1.8& 2.4& 2.0& 1.8\\ q& & & & \\ & 0.98& & & \\ & & 0.95& & \\ & & & 0.80& \end{array}\right],$$
其中空白处为 $0,q$ 是 $0\sim 1$ 岁 (即羊羔) 的存活率, 可以控制。为保持羊群数量 $N$ 不变, 需 满足 $x=Px$, 由此可得

clc,clear,prob=eqnproblem; 
x=optimvar('x',5,'LowerBound',0); % chuan
q=optimvar('q','LowerBound',0);
p=diag([q,0.98,0.95,0.80],-1);
p(1,[2:end])=[1.8,2.4,2.0,1.8];
x0.q=rand;x0.x=rand(5,1);%初值
prob.Equations=[x==p*x;sum(x)==1];
[so1,fval,flag]=solve(prob,x0)
sq=so1.q,sx=so1.x %显示非线性方程组的解

from sympy import *

x = Symbol('x')
y = Symbol('y')
z = Symbol('z')
R = Symbol('R')
G = Symbol('G')
q = Symbol('q')
eq = [0, 1.8, 2.4, 2.0, 1.8], [q, 0, 0, 0, 0], [0, 0.98, 0, 0,0], [0, 0, 0.95, 0, 0], [0, 0, 0, 0.98, 0]
X = [x, y, z, R, G]
Zong = 0
for i in X:
    Zong += i
f1 = Zong - 1
k = []
for i in eq:
    a = 0
    for j in range(len(X)):
        a += i[j] * X[j]
    k.append(a)
print(k)
F = []
for i in range(len(k)):
    F.append(k[i]-X[i])
F.append(f1)

print(solve(F, [x, y, z, R, G, q]))
'''[(0.666943213668971, 0.0871105635147510, 0.0853683522444559, 0.0810999346322331, 0.0794779359395885, 0.130611664875545)]'''

$$q=0.1360,x=[0.6694,0.0871,0.0854,0.0811,0.07948{]}^{\mathrm{T}},$$

可知当 $N$ 不变时每年产羊羔数量为 $0.6694N$, 秋冬季存活的母羊数量为 $0.3306N$ 。
设草场面积为 $S\left({\mathrm{m}}^2\right)$, 根据各个季节草的需求量 $(\mathrm{kg})$ 和生长率, 应有
冬季草的需求量 $2.1\times 0.3306N=0.7056N$,
春季草的需求量 $0.6694N+2.4\times 0.3306N=1.4758N<0.003S$,
夏季草的需求量 $1.65\times 0.6694N+1.15\times 0.3306N=1.4847N<0.007S$,
秋季草的需求量 $1.35\times 0.3306N=0.4463N<0.004S$.
可以算出, 只要春季满足 $N/S<0.002$ (每平方米草地羊的数量), 夏季和秋季都不成问 题。若夏季储存草 $y\mathrm{kg}/{\mathrm{m}}^2$, 保存到冬季用, 则需有 $1.4847N/S<0.007-y$, 其中 $N/S$ 以春 季需满足的数值代人, 可得 $y<0.004\mathrm{kg}/{\mathrm{m}}^2$, 而冬季的粮食需求量是$0.004Skg$, 故夏季的贮藏足够冬季之用。

则$N=0.004S/0.7056=0.0057S$

, 管理者要 估计草场能放牧$0.0057S$只羊, 每年保留$0.3306\times 0.0057S=0.0019S$只母羊羔,夏季要 储藏$0.004Skg$草供冬季之用。