浅谈两种聚类K-Means DBSCAN

wxj1yx

已于 2023-10-27 11:17:24 修改

阅读量147

点赞数 2

文章标签：机器学习算法聚类

于 2023-10-27 11:14:24 首次发布

本文链接：https://blog.csdn.net/wxj1yx/article/details/134071762

版权

浅谈两种聚类K-Means DBSCAN

两种聚类算法:

K-Means K均值算法:

创建k个点作为初始质心(通常随机选择)
当任意一个点的族分配结果发生改变时
1. 对数据集中的每个数据点
  1. 对每个质心
    1. 计算质心与数据点之间的距离
    2. 将数据点分配到距其最近的簇
2. 对于每一个簇, 计算簇中所有点的均值并将均值作为质心
  但有如下缺点:
对超参数K选取敏感
对初始质心点敏感
对异常数据敏感
优点为:
算法运行速度块
对球形簇通常有较好效果

DBSCAN 基于密度的噪声应用空间聚类:
DBSCAN流程:

标记所有对象为unvisited
当有标记对象时
1. 随机选取一个unvisited对象p
2. 标记p为visited
3. 若p的ε领域内至少有M个对象,则
  1. 创建一个新的簇C, 把p放入C中
  2. 设N是p的ε领域内的集合,对于N中每一个点p’
    1. 若p’是unvisited
      1. 标记p’ visited
      2. 若p’的ε领域内至少有M个对象, 则把这些点添加到N
      3. 若p’还不是任何簇的成员, 则把p’添加到C
  3. 保存C
4. 否则标记p为噪声
  有如下缺点:
需要提前确定ε,M的值
对初值选取敏感
优点为:
不需要提前设置簇的个数
对噪声不敏感
对各种形状的簇都有较好的效果
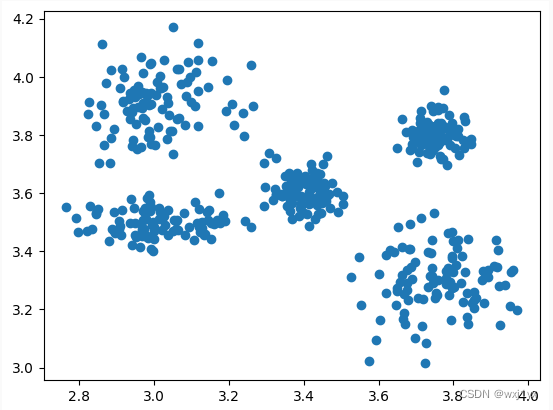
接下来生成一些点测试一下K-means, DBSCAN的性能
首先根据设置5个不同的均值和方差生成一些具有5个中心分布特征的二维样本点

#生成size个高斯分布点
def GaussDistribution(size, mu, sigma):
    return random.normal(mu, sigma, size)

def getSamplesForkMeans():
    size = 100
    sample = np.zeros((5 * size, 2))
    mu, sigma = 3.75, 0.1
    sample[0:size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.3
    sigma = 0.1
    sample[0:size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.75
    sigma = 0.05
    sample[size:2 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.8
    sigma = 0.05
    sample[size:2 * size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.0
    sigma = 0.1
    sample[2 * size:3 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.9
    sigma = 0.1
    sample[2 * size:3 * size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.0
    sigma = 0.1
    sample[3 * size:4 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.5
    sigma = 0.05
    sample[3 * size:4 * size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.4
    sigma = 0.05
    sample[4 * size:5 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.6
    sigma = 0.05
    sample[4 * size:5 * size, 1] = GaussDistribution(size, mu, sigma)
    return sample;

samples = getSamplesForkMeans()
np.shape(samples)
#绘制样本点
plt.scatter(samples[:, 0], samples[:, 1])
plt.show()

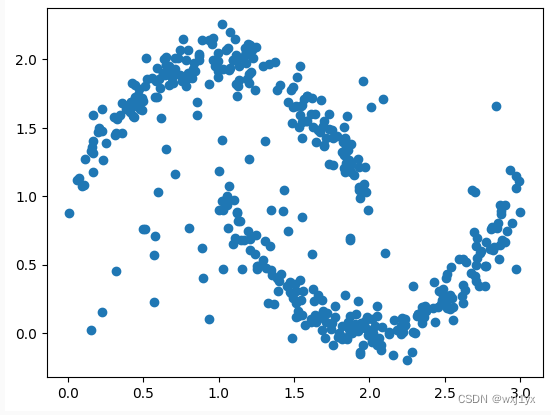
请添加图片描述

在两个二次曲线附近生成随机点, 并添加一些离群点

def getSamplesForDBSCAN():
    def f1(x):
        return -((x - 1)**2) + 2
    def f2(x):
        return (x - 2) ** 2
    size = 200
    sample = np.zeros((420, 2))
    for i in range(size):
        sample[i, 0] = random.uniform(0, 2)
        sample[i, 1] = f1(sample[i, 0]) + GaussDistribution(1, 0, 0.11)
    for i in range(size, 2 * size):
        sample[i, 0] = random.uniform(1, 3)
        sample[i, 1] = f2(sample[i, 0]) + GaussDistribution(1, 0, 0.11)
	# 添加离群点
    for i in range(2*size, 420):
        sample[i, 0] = random.uniform(0, 3)
        sample[i, 1] = random.uniform(0, 2)
    return sample

samples_DBSCAN = getSamplesForDBSCAN()
#绘制样本点
plt.scatter(samples_DBSCAN[:, 0], samples_DBSCAN[:, 1])
plt.show()

请添加图片描述

K-Means ( 具体实现见附录)

使用欧式距离进行距离度量

$dist_{eucl}(vecA, vecB) = \sqrt{\Sigma_i(vecA_i-vecB_i)^2}$

ks = [ i for i in range(2, 20)]
SSEs = []
for k in ks:
    centroids, clusterAssment = k_means(samples, k, 'dist_eucl', 'asc')
    SSEs.append(SSE(clusterAssment))
plt.plot(ks, SSEs)

通过测试不同取值下均方差SSE的变化来确定k的合适取值
$\Sigma dist(s_i,c^i)^2$
即每个样本点到其中心的距离的平方和
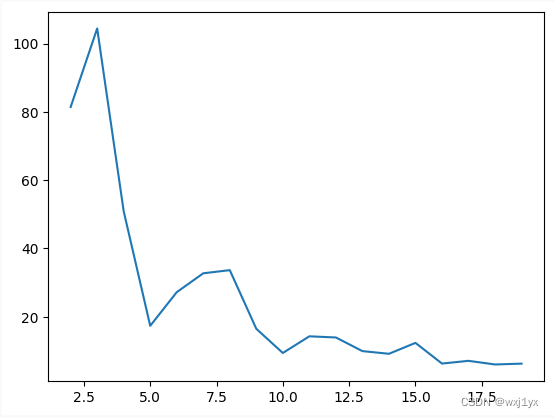
请添加图片描述

由于K-Means的初值敏感性所以会出现些许震荡, 但仍可以大致确定当k = 5时能够取得较好效果
当k大于5时并不能有效改善均方差, 但运行时间却无节制地增长
此时聚类得到的图谱:
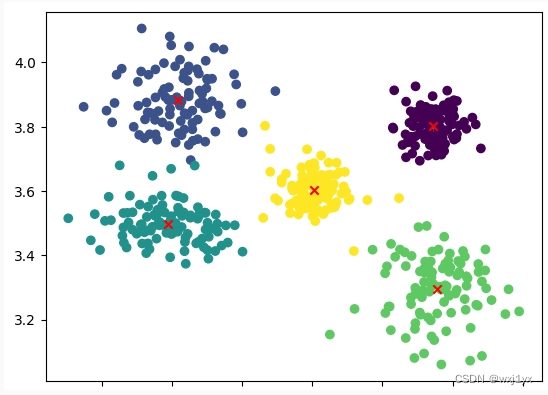
请添加图片描述

centroids, clusterAssment = k_means(samples, 5, 'dist_eucl', 'asc')
#绘制样本点
plt.scatter(samples[:, 0], samples[:, 1], c = clusterAssment[:, 0])

我用不同颜色表示不同的簇, 用x表示最终收敛得到的聚类中心。这看起来得到了预期的结果, 但是为了测试K-Means的稳定性, 我将在统一k值下多次测试K-Means的均方差结果:

SSEs = []
for i in range(10):
    centroids, clusterAssment = k_means(samples, 5, 'dist_eucl', 'asc')
    SSEs.append(SSE(clusterAssment))
plt.plot([i for i in range(10)], SSEs)
plt.title('Std: %f Mean: %f' % (np.std(SSEs), np.mean(SSEs)))
plt.show()

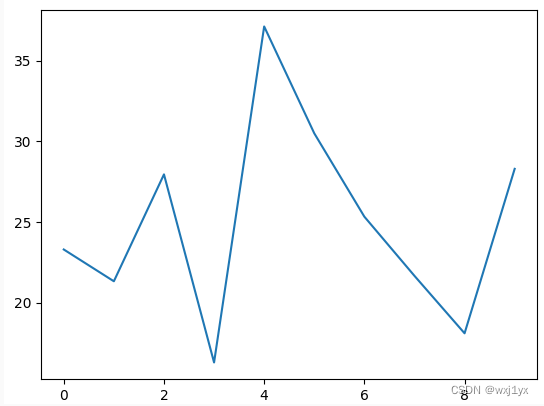
请添加图片描述

可以见到即使在同一k值下也获得了相差十分巨大的结果, 其中两次聚类结果展示如下:
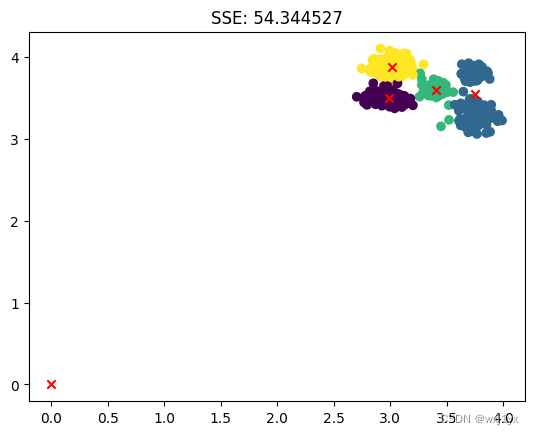
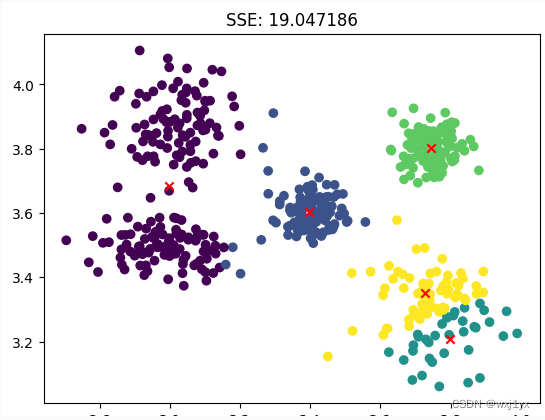
请添加图片描述

以上两种情况就足够说明在同一k值下K-Means聚类算法对初始中心值的随机选取的非常敏感的了，第一种情况有一个中心值停留在了0，0处，这意味着没有任何一个样本点在初始化中被归为这一中心值附近，也意味着这个中心值在初始化时就出生在了离大多数点都很远的“偏僻位置”.
第二种情况虽然被划分为了五个簇, 甚至得到了SSE比我们之前得到的还要小, 但这不是我们想要的结果, 由此可见, SSE并不能特别好的作为聚类效果好坏的衡量标准，尽管他在大多数时候可以让我们在短时间内判断最佳k值的选择。
K-Means算法的初值敏感性很大程度上决定于初始中心点生成的算法, 他仅仅只是在以所有样本点的每个维度上的最大-最小值所围成的包围盒中随机初始化k个点, 这并未充分考虑样本点的分布特性, 因为这个包围盒的范围很容易受某些稀疏的, 离群的点影响。所以在K-Means++算法中不再这样选取初值， K-Means++算法以某些样本点为初始中心，这样中心点就容易“出生”在样本点密度高的地方，因此稳定性也获得上升，篇幅有限这里就不再进行测试了。
接下来我们测试另一种相似度度量方法：余弦相似度

使用余弦相似度进行距离度量

$dist_{cos}(vecA, vecB) = \frac{vecA ·vecB}{|vecA||vecB|}$

centroids, clusterAssment = k_means(newsamples, 5, 'dist_cos', 'desc')
#绘制样本点
plt.xlim((0, 1.75))
plt.ylim((0, 1.75))
plt.scatter(newsamples[:, 0], newsamples[:, 1], c = clusterAssment[:, 0])
plt.scatter(centroids[:, 0], centroids[:, 1], c = 'r', marker = 'x')
plt.title('SSE: %f' % SSE(clusterAssment))

为了将样本点离原点更近方便观察, 我们将所有样本的x,y轴都往负半轴平移了2.5个单位再进行聚类,得到了如下的聚类结果
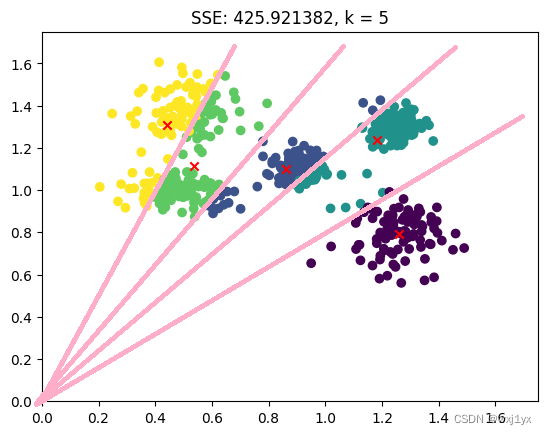
请添加图片描述

为了方便观察我添加了几条辅助线，可以见到，簇的划分边界正是这些线，此时K-Means的聚类形状并不是球形，但如果将这些点映射到极坐标系中呢。

newsamples_Polar = toPolar(newsamples)
centroids_Polar = toPolar(centroids)
plt.scatter(newsamples_Polar[:, 0], newsamples_Polar[:, 1], c = clusterAssment[:, 0])
plt.scatter(centroids_Polar[:, 0], centroids_Polar[:, 1], c = 'r', marker = 'x')
plt.title('SSE: %f, k = 5' % SSE(clusterAssment))
plt.show()

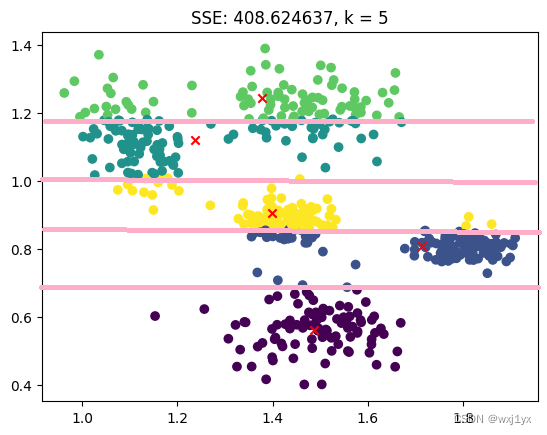
请添加图片描述

在极坐标空间里他仍然不是球形簇，而是出现分层, 并且我们在计算质心时只是简单的取平均而导致其中有一点点不严谨的地方, 对于以余弦相似度为度量标准时的K-Means算法应当使用余弦质心来替代平均值质心的计算。余弦质心的推导过程十分复杂, 可以参考资料：k-means 聚类中使用余弦距离 cos distance - 知乎 (zhihu.com)
不过我们都可以可以观察到SSE很大, 这是因为相似性越高反应的余弦值越大, 所以SSE约大是越好的。
同样地，调整不同k值观察k对SSE的影响。
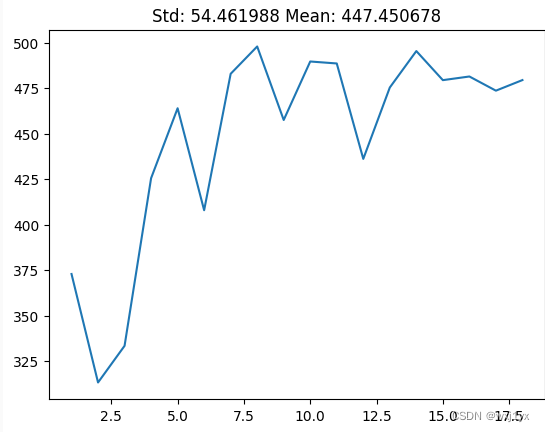
请添加图片描述

虽然仍然有波动但是总体而言随K值增大SSE是增加的, 这意味着类内相似度是增大的。可见，随着中心点数的增加，类内相似度是会增大的。

DBSCAN (具体实现见附录)

C = dbscan(samples_DBSCAN, 0.2, 5)
plt.scatter(samples_DBSCAN[:, 0], samples_DBSCAN[:, 1], c = C)
plt.show()

选取ε = 0.2, M = 5可以得到如下图像:
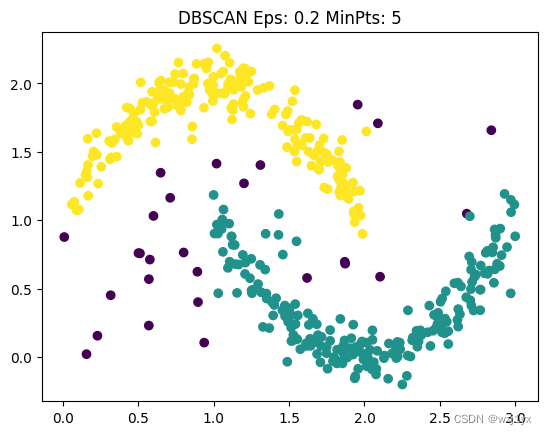
请添加图片描述

其中紫色点为离群点。我们同样获得了理想的效果，接下来让ε = 0.1，
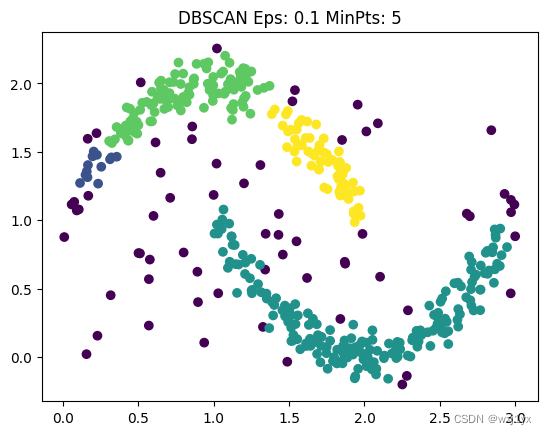
请添加图片描述

这样效果就没那么好了，上方的月牙形状被分为了不同的簇，并且更多的点被分为了离群点。
保持ε不变，减小M：
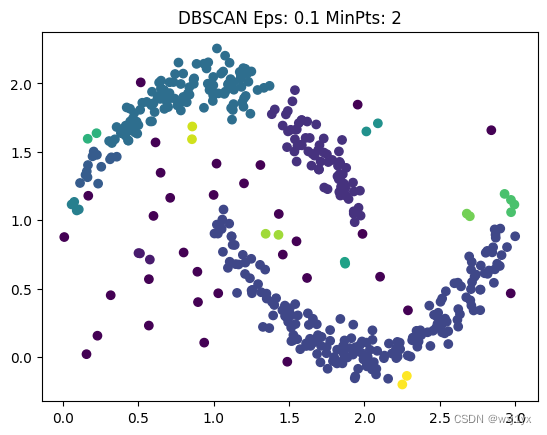
请添加图片描述
让ε = 0.2， M = 20：

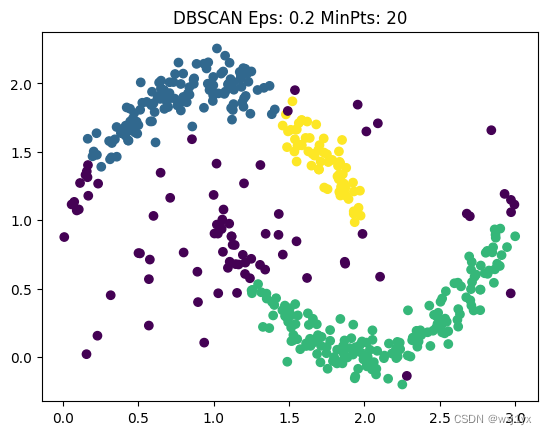
可以简单地总结出： ε越大，聚类图形越完整，面积越大， ε越小，聚类图形越破碎，M则反之。

六种衡量聚类效果指标:

戴维森堡丁指数 Davies-Bouldin Index (DBI)
DBI计算任意两类别的类内距离平均距离(CP)之和除以两聚类中心距离求最大值。DB越小意味着类内距离越小同时类间距离越大。
$\frac{1}{N} \Sigma \max_{j ≠ i}(\frac{\bar{S_i} + \bar{S_j}}{||\omega_i -\omega_j||^2})$
轮廓系数 Silhouette Coefficient s(i):

$\frac{b(i) - a(i)}{\max(a(i), b(i))}, s(i) = \begin{cases} 1 - \frac{a_i}{b_i}, a(i) < b(i) \\ 0, a(i) = b(i) \\ \frac{b(i)}{a(i)} - 1, a(i) > b(i) \end{cases}$
$\begin{equation} a(i) = \frac{1}{n - 1} \Sigma_{i ≠ j}^{n}distance(i, j), j为与i统一簇的非i点 \end{equation}$
$min_i(b_{i1}, b_{i2},..., b_{ix}), x ≠ i, b_{ix} = \frac{1}{m-1}\Sigma_{k}^{m}distance(i, k), k为第x簇的某一点$
$a_i$ 被称为样本i的簇内不相似度, $b_i$ 被称为样本i与簇Cj 的不相似度,某一个簇C中所有样本的 $a_i$ 均值称为簇C的簇不相似度。
最终整个数据的轮廓系数=每个样本轮廓系数之和/n(即所有样本轮廓系数的平均值)

邓恩指数 Dunn Validity Index D:
$\frac{\min_{i \neq j} d(C_i, C_j)}{\max_{k} d(C_k)}$
其中， $C_i$ 表示第 $i$ 个簇， $d(C_i, C_j)$ 表示簇 $C_i$ 和簇 $C_j$ 之间的距离， $d(C_k)$ 表示簇 $C_k$ 内部样本之间的最大距离。
它基于聚类内部的紧密度和聚类之间的分离度，值越大表示聚类效果越好。具体来说，邓恩指数定义为最近簇之间距离的最小值与最远簇内部距离的最大值的比值。也就是说，邓恩指数越大，表示簇内部的样本越紧密，簇之间的样本越分散，聚类效果越好。
标准化互信息 Normalized MutualInformation NMI(Ω, C):

$NMI(\Omega, C) = \frac{I(\Omega;C)}{(H(\Omega) + H(C)/2)}$

调整互信息 Adjusted MutualInformation AMI:
$\frac{MI - E[MI]}{\max(H(U), H(V) - E([MI]))}$
调整兰德指数 Adiusted Rand index ARI:
$\frac{RI - E[RI]}{\max(RI) - E[RI]}$

这里仅对比不同k值下以欧式距离为距离度量方法的K-Means聚类结果的轮廓系数，邓恩指数以及标准化后的SSE（Sum Squared Error)
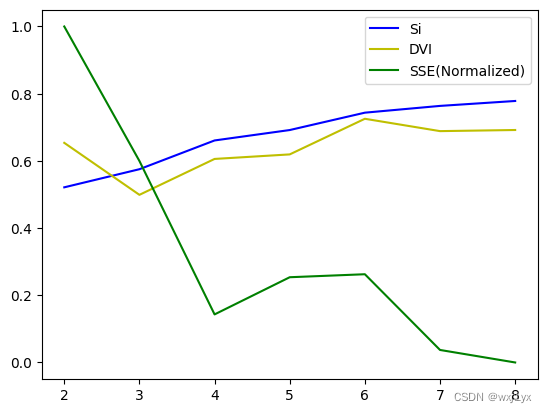
请添加图片描述

参考资料:
常用聚类算法 - 知乎 (zhihu.com))
聚类算法评价指标——Davies-Bouldin指数(Dbi)_davies-bouldin index-CSDN博客
 聚类效果评估指标总结_轮廓系数为多少说明聚类有效-CSDN博客
 聚类效果评估——轮廓系数（Silhouette Coefficient）附Python代码-CSDN博客
 Dunn Index：放弃西瓜书定义，拥抱Wikipedia定义 - 知乎 (zhihu.com)
聚类效果评价指标：MI, NMI, AMI（互信息，标准化互信息，调整互信息）_nmi评价指标-CSDN博客
 聚类算法评价指标——adjusted Rand index, ARI指数(调整兰德指数)-CSDN博客

附录

import numpy as np
import numpy.random as random
import matplotlib.pyplot as plt
import seaborn as sns

#生成size个高斯分布点
def GaussDistribution(size, mu, sigma):
    return random.normal(mu, sigma, size)

def getSamplesForkMeans():
    size = 100
    sample = np.zeros((5 * size, 2))
    mu, sigma = 3.75, 0.1
    sample[0:size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.3
    sigma = 0.1
    sample[0:size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.75
    sigma = 0.05
    sample[size:2 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.8
    sigma = 0.05
    sample[size:2 * size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.0
    sigma = 0.1
    sample[2 * size:3 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.9
    sigma = 0.1
    sample[2 * size:3 * size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.0
    sigma = 0.1
    sample[3 * size:4 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.5
    sigma = 0.05
    sample[3 * size:4 * size, 1] = GaussDistribution(size, mu, sigma)
    mu = 3.4
    sigma = 0.05
    sample[4 * size:5 * size, 0] = GaussDistribution(size, mu, sigma)
    mu = 3.6
    sigma = 0.05
    sample[4 * size:5 * size, 1] = GaussDistribution(size, mu, sigma)
    return sample;

samples = getSamplesForkMeans()
#绘制样本点
plt.scatter(samples[:, 0], samples[:, 1])
plt.show()

def getSamplesForDBSCAN():
    def f1(x):
        return -((x - 1)**2) + 2
    def f2(x):
        return (x - 2) ** 2
    size = 200
    sample = np.zeros((420, 2))
    for i in range(size):
        sample[i, 0] = random.uniform(0, 2)
        sample[i, 1] = f1(sample[i, 0]) + GaussDistribution(1, 0, 0.11)
    for i in range(size, 2 * size):
        sample[i, 0] = random.uniform(1, 3)
        sample[i, 1] = f2(sample[i, 0]) + GaussDistribution(1, 0, 0.11)

    for i in range(2*size, 420):
        sample[i, 0] = random.uniform(0, 3)
        sample[i, 1] = random.uniform(0, 2)
    return sample

samples_DBSCAN = getSamplesForDBSCAN()
#绘制样本点
plt.scatter(samples_DBSCAN[:, 0], samples_DBSCAN[:, 1])
plt.show()

def rand_center(dataSet, k):
    """构建一个包含K个随机质心的集合"""
    n = np.shape(dataSet)[1] # 获取样本特征值
    centroids = np.array(np.zeros((k, n))) # 每个质心有n个坐标值，总共要k个质心
    if not dataSet.any():
        return centroids
    # 遍历特征值
    for j in range(n):
        minJ = np.min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ)
        if rangeJ:
            centroids[:, j] = (minJ + rangeJ * random.rand(k, 1)).squeeze()
    return centroids # 返回质心

def k_means_asc(dataSet, k, distMeas, creatCent):
    m = np.shape(dataSet)[0] # 行数
    # 建立簇分配结果矩阵，第一列存放该数据所属中心点，第二列是该数据到中心点的距离
    clusterAssment = np.array(np.zeros((m, 2)))
    centroids = eval(creatCent)(dataSet, k) # 质心，即聚类点
    # 用来判定聚类是否收敛
    clusterChanged = True
    n = 0;
    while clusterChanged:
        clusterChanged = False
        for i in range(m): # 把每一个数据划分到离他最近的中心点
            minDist = 1e9 # 无穷大
            minIndex = -1 # 初始化
            vec2 = dataSet[i, :]
            for j in range(k):
                # 计算各点与新的聚类中心的距离
                vec1 = centroids[j, :]
                distJI = eval(distMeas)(vec1, vec2)
                if minDist > distJI:
                    # 如果第i个数据点到第j中心点更近，则将i归属为j
                    minDist = distJI
                    minIndex = j
            # 如果分配发生变化，则需要继续迭代
            if clusterAssment[i, 0] != minIndex:
                clusterChanged = True
                # 并将第i个数据点的分配情况存入字典
                clusterAssment[i, :] = minIndex, minDist ** 2
        for cent in range(k): # 重新计算中心点
            # 取第一列等于cent的所有列
            ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0] == cent)[0]]
            # 算出这些数据的中心点
            if not ptsInClust.any():
                centroids[cent, :] = 0
            else:
                centroids[cent, :] = np.mean(ptsInClust, axis=0)
    return centroids, clusterAssment

def k_means_desc(dataSet, k, distMeas, creatCent):
    m = np.shape(dataSet)[0] # 行数
    # 建立簇分配结果矩阵，第一列存放该数据所属中心点，第二列是该数据到中心点的距离
    clusterAssment = np.array(np.zeros((m, 2)))
    centroids = eval(creatCent)(dataSet, k) # 质心，即聚类点
    # 用来判定聚类是否收敛
    clusterChanged = True
    n = 0;
    while clusterChanged:
        clusterChanged = False
        for i in range(m): # 把每一个数据划分到离他最近的中心点
            minDist = 0 # 无穷大
            minIndex = -1 # 初始化
            vec2 = dataSet[i, :]
            for j in range(k):
                # 计算各点与新的聚类中心的距离
                vec1 = centroids[j, :]
                distJI = eval(distMeas)(vec1, vec2)
                if minDist < distJI:
                    # 如果第i个数据点到第j中心点更近，则将i归属为j
                    minDist = distJI
                    minIndex = j
            # 如果分配发生变化，则需要继续迭代
            if clusterAssment[i, 0] != minIndex:
                clusterChanged = True
                # 并将第i个数据点的分配情况存入字典
                clusterAssment[i, :] = minIndex, minDist ** 2
        for cent in range(k): # 重新计算中心点
            # 取第一列等于cent的所有列
            ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0] == cent)[0]]
            # 算出这些数据的中心点
            if not ptsInClust.any():
                centroids[cent, :] = 0
            else:
                centroids[cent, :] = np.mean(ptsInClust, axis=0)
    return centroids, clusterAssment
  
def k_means(dataSet, k, distMeas, order = 'asc', creatCent = 'rand_center'):
    if order == 'asc':
        return k_means_asc(dataSet, k, distMeas, creatCent)
    elif order == 'desc':
        return k_means_desc(dataSet, k, distMeas, creatCent)
    else :
        return None, None
        
def dist_eucl(vecA, vecB):
    return np.sqrt(np.sum(np.power(vecA - vecB, 2)))

def dist_cos(vecA, vecB):
    return np.sum(vecA * vecB) / (np.linalg.norm(vecA) * np.linalg.norm(vecB))

def SSE(clusterAssment):
    sse = 0
    for i in range(clusterAssment.shape[0]):
        sse += np.sum(clusterAssment[np.nonzero(clusterAssment[:, 0] == i)[0], 1])
    return sse

ks = [ i for i in range(2, 20)]
SSEs = []
for k in ks:
    centroids, clusterAssment = k_means(samples, k, 'dist_eucl', 'asc')
    SSEs.append(SSE(clusterAssment))
plt.xlim(2, 22)
plt.plot(ks, SSEs)
plt.show()

centroids, clusterAssment = k_means(samples, 5, 'dist_eucl', 'asc')
#绘制样本点
plt.scatter(samples[:, 0], samples[:, 1], c = clusterAssment[:, 0])
plt.scatter(centroids[:, 0], centroids[:, 1], c = 'r', marker = 'x')
plt.title('SSE: %f' % SSE(clusterAssment))

SSEs = []
for i in range(10):
    centroids, clusterAssment = k_means(samples, 5, 'dist_eucl', 'asc')
    SSEs.append(SSE(clusterAssment))
plt.plot([i for i in range(10)], SSEs)
plt.title('Std: %f Mean: %f' % (np.std(SSEs), np.mean(SSEs)))
plt.show()

newsamples = samples.copy()
newsamples[:, 0] -= 2.5
newsamples[:, 1] -= 2.5
centroids, clusterAssment = k_means(newsamples, 5, 'dist_cos', 'desc')
#绘制样本点
plt.xlim((0, 1.75))
plt.ylim((0, 1.75))
plt.scatter(newsamples[:, 0], newsamples[:, 1], c = clusterAssment[:, 0])
plt.scatter(centroids[:, 0], centroids[:, 1], c = 'r', marker = 'x')
plt.title('SSE: %f, k = 5' % SSE(clusterAssment))

def toPolar(dataset):
    polar = np.zeros((dataset.shape[0], 2))
    for i in range(dataset.shape[0]):
        polar[i, 0] = np.sqrt(dataset[i, 0] ** 2 + dataset[i, 1] ** 2) # rho
        polar[i, 1] = np.arctan(dataset[i, 1] / dataset[i, 0]) # theta
    return polar

newsamples_Polar = toPolar(newsamples)
centroids_Polar = toPolar(centroids)
plt.scatter(newsamples_Polar[:, 0], newsamples_Polar[:, 1], c = clusterAssment[:, 0])
plt.scatter(centroids_Polar[:, 0], centroids_Polar[:, 1], c = 'r', marker = 'x')
plt.title('SSE: %f, k = 5' % SSE(clusterAssment))
plt.show()

SSEs = []
for k in ks:
    centroids, clusterAssment = k_means(newsamples, k, 'dist_cos', 'desc')
    SSEs.append(SSE(clusterAssment))
plt.plot([i for i in range(1, 1 + len(SSEs))], SSEs)
plt.title('Std: %f Mean: %f' % (np.std(SSEs), np.mean(SSEs)))
plt.show()

from scipy.spatial import KDTree

class visitlist:
    """
        visitlist类用于记录访问列表
        unvisitedlist记录未访问过的点
        visitedlist记录已访问过的点
        unvisitednum记录访问过的点数量
    """
    def __init__(self, count=0):
        self.unvisitedlist=[i for i in range(count)]
        self.visitedlist=list()
        self.unvisitednum=count

    def visit(self, pointId):
        self.visitedlist.append(pointId)
        self.unvisitedlist.remove(pointId)
        self.unvisitednum -= 

def dist(a, b):
    """
    @brief      计算a,b两个元组的欧几里得距离
    @param      a    
    @param      b    
    @return     距离
    """
    return np.sqrt(np.power(a-b, 2).sum())
  
def dbscan(dataSet, eps, minPts):
    """
    @brief      基于kd-tree的DBScan算法
    @param      dataSet  输入数据集，numpy格式
    @param      eps      最短距离
    @param      minPts   最小簇点数
    @return     分类标签
    """
    nPoints = dataSet.shape[0]
    vPoints = visitlist(count=nPoints)
    # 初始化簇标记列表C，簇标记为 k
    k = -1
    C = [-1 for i in range(nPoints)]
    # 构建KD-Tree，并生成所有距离<=eps的点集合
    kd = KDTree(dataSet)
    while(vPoints.unvisitednum>0):
        p = random.choice(vPoints.unvisitedlist)
        vPoints.visit(p)
        N = kd.query_ball_point(dataSet[p], eps)
        if len(N) >= minPts:
            k += 1
            C[p] = k
            for p1 in N:
                if p1 in vPoints.unvisitedlist:
                    vPoints.visit(p1)
                    M = kd.query_ball_point(dataSet[p1], eps)
                    if len(M) >= minPts:
                        for i in M:
                            if i not in N:
                                N.append(i)
                    if C[p1] == -1:
                        C[p1] = k
        else:
            C[p] = -1
    return C

C = dbscan(samples_DBSCAN, 0.2, 20)
plt.scatter(samples_DBSCAN[:, 0], samples_DBSCAN[:, 1], c = C)
plt.title('DBSCAN Eps: 0.2 MinPts: 20')
plt.show()

from sklearn.metrics import pairwise_distances
def DBI(samples, labels):
    n = samples.shape[0]
    k = len(set(labels))
    len(set(labels))
    centers = np.zeros((k, samples.shape[1]))
    # 计算每个簇的紧密度
    intra_cluster_distances = np.zeros(k)
    for i in range(k):
        intra_cluster_distances[i] = np.mean(pairwise_distances(samples[labels == i], [centers[i]], metric='euclidean'))
    # 计算聚类之间的分离度
    separation_matrix = pairwise_distances(centers, metric='euclidean')
    np.fill_diagonal(separation_matrix, np.inf)
    inter_cluster_distances = np.max(separation_matrix, axis=1)
    # 计算DBI
    dbi = np.mean((intra_cluster_distances + inter_cluster_distances) / intra_cluster_distances)
    return dbi

  

def Si(samples, labels):
    # 计算每个样本的轮廓系数
    n_samples = len(samples)
    s = np.zeros(n_samples)
    for i in range(n_samples):
        a_i = np.mean(pairwise_distances(samples[i].reshape(1, -1), samples[labels == labels[i]], metric='euclidean'))
        b_i = np.min(np.mean(pairwise_distances(samples[i].reshape(1, -1), samples[labels != labels[i]], metric='euclidean')))
        s_i = (b_i - a_i) / max(a_i, b_i)
        s[i] = s_i
    # 计算整个数据集的平均轮廓系数
    si = np.mean(s)
    return si
  
def DVI(samples, labels):
    # 计算每个簇的中心点
    n_clusters = len(set(labels))
    cluster_centers = np.zeros((n_clusters, samples.shape[1]))
    for i in range(n_clusters):
        cluster_centers[i] = np.mean(samples[labels == i], axis=0)
    # 计算聚类之间的距离
    separation_matrix = pairwise_distances(cluster_centers, metric='euclidean')
    np.fill_diagonal(separation_matrix, np.inf)
    # 计算簇内最大距离和簇间最小距离
    max_intra_cluster_distance = np.zeros(n_clusters)
    min_inter_cluster_distance = np.min(separation_matrix, axis=1)
    for i in range(n_clusters):
        max_intra_cluster_distance[i] = np.max(pairwise_distances(samples[labels == i], metric='euclidean'))
    # 计算邓恩指数
    dvi = np.mean(min_inter_cluster_distance / max_intra_cluster_distance)
    return dvi

DBIs, Sis, DVIs, SSEs = [], [], [], []
ks = [2, 3, 4, 5, 6, 7, 8]
for k in [2, 3, 4, 5, 6, 7, 8]:
    centroids, clusterAssment = k_means(samples_DBSCAN, k, 'dist_eucl', 'asc')
    DBIs.append(DBI(samples_DBSCAN, clusterAssment[:, 0]))
    Sis.append(Si(samples_DBSCAN, clusterAssment[:, 0]))
    DVIs.append(DVI(samples_DBSCAN, clusterAssment[:, 0]))
    SSEs.append(SSE(clusterAssment))
plt.plot(ks, Sis, label='Si', c = 'b')
plt.plot(ks, DVIs, label='DVI', c = 'y')
SSEs = MaxMinNormalization(np.array(SSEs))
plt.plot(ks, SSEs, label='SSE(Normalized)', c = 'g')
plt.legend()
plt.show()
 max_intra_cluster_distance)
    return dvi

DBIs, Sis, DVIs, SSEs = [], [], [], []
ks = [2, 3, 4, 5, 6, 7, 8]
for k in [2, 3, 4, 5, 6, 7, 8]:
    centroids, clusterAssment = k_means(samples_DBSCAN, k, 'dist_eucl', 'asc')
    DBIs.append(DBI(samples_DBSCAN, clusterAssment[:, 0]))
    Sis.append(Si(samples_DBSCAN, clusterAssment[:, 0]))
    DVIs.append(DVI(samples_DBSCAN, clusterAssment[:, 0]))
    SSEs.append(SSE(clusterAssment))
plt.plot(ks, Sis, label='Si', c = 'b')
plt.plot(ks, DVIs, label='DVI', c = 'y')
SSEs = MaxMinNormalization(np.array(SSEs))
plt.plot(ks, SSEs, label='SSE(Normalized)', c = 'g')
plt.legend()
plt.show()