青蛙跳台阶：我如何得知它是一道斐波那契数列题？——应用题破题“三板斧”

本文以C语言实现。

---

目录

前言

一、斐波那契阿数列基础知识

二、引例：青蛙跳台阶

三、破题分析：举例归纳

1. 三板斧的使用

举例

模拟（必要时画图）

找规律

2. 代码展示 

四、拓展用例：矩形覆盖问题

三板斧的使用

举例

模拟

找规律

五、总结

---

前言

C语言初学者在学习“递归与循环”章节时，一定会遇到“不死兔子”这道经典例题。

 简而言之，它就是一个数列，除了第一项与第二项值为1以外，所有的项的值都等于其前两项的值之和：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）

在编程学习中，当单考斐波那契数列，即题目直接要求编写斐波那契数列代码时，许多同学并不会被难到。然而，当题干转变提问思路，转而提问“青蛙跳台阶有几种跳法”“小矩形摆大矩形有几种摆法”时，许多人就懵了：没有意识到其实这样的题干本质上还是在考察斐波那契数列的实现。

是的，斐波那契数列考题（或者说有很多的应用题），难点或许并不在代码实现，而在如何从看似有些“莫名其妙”的题干中分析出，这是一道考xxx的例题。

一些同学疑惑，自己怎么能想到用斐波那契数列求解呢？事实上，我们只需要会分析出恰当的办法解出来就好了，而不必纠结于“我看不出这用斐波那契写啊，那我就不会做了”。分析的过程是最重要的，无非是我们经过一番分析发现，恰好我们的解题思路和斐波那契一样，而不是早就知道了用这个方法，然后往题目里套。 

因而，本文以应用题“青蛙跳台阶”为引例，讲解如何破题并分析出题干背后的考点；并在文末贴上另一道相对而言少见的相关题目：矩形覆盖问题。

这两道题都将附上详解，希望各位读者能有所收获。

---

一、斐波那契阿数列基础知识

本文默认大家都熟悉斐波那契数列的基础知识：包括最基础的代码编写思路和具体实现。不过还是考虑到也许一些同学一下子反应不过来把基础知识给忘了，因而在正文开始前，先贴上斐波那契数列的代码实现。不需要的同学可以直接跳过。

1. 斐波那契数列定义：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）

2. 求斐波那契数列的第N项

//求Fib数列第n项

//非递归
int main(){
    int f1 = 1;
    int f2 = 1;
    int fn,n;

    scanf("%d",&n);
    
    for(int i = 3; i <= n; i++){
        fn = f1 + f2;
        f1 = f2;
        f2 = fn;
    }

    printf("%d",fn);

    return 0;
}

//递归
int Fib(int n){
    if(n <= 0){
        return 0;
    }
    
    if(n == 1){
        return 1;
    }

    return Fib(n - 1) + Fib(n - 2)
}

3. 实现思路 

从Fib的数学定义可以非常简单地得出递归思路：除了第1项和第2项值为1（第0项或负数项，这里默认为0），所有的项的值都是前两项之和F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)

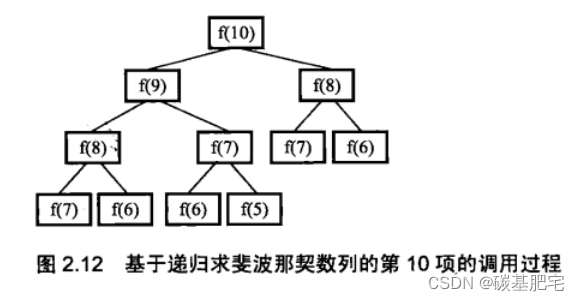
非递归的思路类似于“滚车轮”，示意图如下：

如图：通过f1 = f2;f2 = fn实现迭代

f1和f2像两只“脚”，通过将三个数中的后一个赋值给前一个，实现整体向右不断叠加计算。 

基础铺垫的部分简单地说明到这里，如果还有朋友们有不理解的地方，可以移步别的博主的优秀解析。本文在此不再赘述。

---

二、引例：青蛙跳台阶

牛客网习题链接

BC117 小乐乐走台阶https://www.nowcoder.com/practice/ebf04de0e02c486099d78b7c3aaec255?tpId=107&&tqId=33398&rp=1&ru=/ta/beginner-programmers&qru=/ta/beginner-programmers/question-ranking

题干如下

题感较好或是曾经刷到过该题的同学应当一眼就能看出，该题就是斐波那契数列的经典习题。事实上题目暗示的也很明确：“一次可以走1级或2级台阶”“一共有多少种走法”。在谈到“一共有多少种办法”的时候，也许想到不断叠加是一件很自然的事情；或者干脆直接死记硬背地记住。从单题的角度看，固然是可行的，但对大多数第一次接触的同学而言，这样的解释和“马后炮”一样，并不靠谱。

采取上述方法的同学可以先尝试直接跳到最后的拓展例题（如果没接触那个例题的话），或者思考如果自己并不提前知道这两道应用题的解法而是从头分析，能不能分析出来。如果不能，那么以上的方式或许就有些欠妥（当然，应付学校的考试是没问题的）。

在分析问题时，我们一般采用这样的方法：题目表意 ----> 模型 ----> 代码，即从题干字面意思中转换成解题的模型（姑且这么叫吧），然后再根据模型逐步求精，编写代码。下面就第一步 表意--模型，展开详细的介绍。

---

三、破题分析：举例归纳

在应用题上格外适用的三板斧：举例，模拟，找规律。

这么做的目的不是直接写出解题代码，而是确定这个题目想要考什么。这个“考什么”不一定和本题一样，可以归纳成一个具体的考点；但一定能根据题意归纳出对应的功能模块。在确定了功能模块，就不愁不会写代码了。毕竟，代码只是把用中文描述的功能模块的逻辑，“翻译”成计算机能看懂的语言。

一定要自己举例+模拟，或是勤动笔去画图（尤其在数据结构那块）。这样是保证找到的规律最正确的方式，尤其在应用题中格外适用。其实对很多人而言，这三板斧并不是信手拈来的，而是需要经过有意识地训练来得到。

1. 三板斧的使用

小乐乐上课需要走n阶台阶，因为他腿比较长，所以每次可以选择走一阶或者走两阶，那么他一共有多少种走法？

举例

直接假设n为5，一共有5级台阶要走。举例就是直接把未知数具体化，代个值进去。

示意

---

模拟（必要时画图）

我们可以有两种考虑思路。这两种本文都会详细介绍，不需要刻意死记硬背，选择自己好理解的思路即可。

思路一

我们能很快看出，这是一个带有循环或者递归性质的问题：走楼梯就是一个不断重复的过程，要问走到第5级台阶有几种方法，思路本质上和走第4级、第3级、第2级、第1级有几种方法肯定是一样的。

我们不妨从最后一个（第5级）开始考虑。

1. 当我们走上第5级台阶的时候，我们上一个走过的台阶可能是哪一级？

-- 第4级或第3级，因为题目里说一次可以跨2级也可以跨1级。

2. 走到第5级用了几种办法，可以看作走到第4级的方法数＋走到第3级的方法数。

3. 第4级又有可能是从第3级或者第2级踏上来的；

4. 第3级又有可能是从第2级或第1级踏上来的，因此可以画出如下示意图：

此时只需要考虑走到第1级和第2级台阶有多少种方法即可

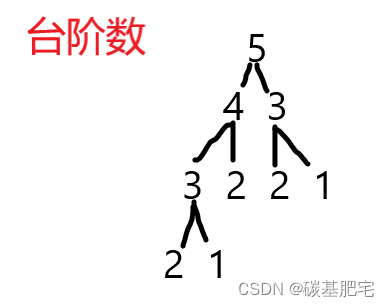
5. 走到第1级台阶，有1种方法，记为f(1)。（从0开始走1级）

6.走到第2级台阶，有2种方法，记为f(2)。（从0开始走1级，或从0开始走2级）。

那么就有：

f(5) = f(4)+f(3)

f(5) = f(3)+f(2) + f(2)+f(1)

f(5) = f(2)+f(1) + f(2)  +  f(2)+f(1)

已知 f(2) = 2，f(1) = 1，有f(5) = 2+1+2+2+1 = 8,即跨上5级台阶，有8种办法。

至此，我们求出了在具体的一个情境中，这道题的解。下面我们只需要根据该特解，归纳推导出该解的通项即可。

---

思路二：

首先我们考虑最简单的情况。

如果只有1级台阶，那只有1种跳法。如果有2级台阶，那就有2种跳的方法了：一种是分两次跳，每次跳1级；另外一种就是一次跳2级。即：

f(1) = 1

f(2) = 2

接着我们再来讨论一般情况。 我们把n级台阶时的跳法记为f(n)。 当n>2时，第一次跳的时候就有两种不同的选择：

是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；

另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。

因此，n级台阶的不同跳法的总数 f(n)=f(n- 1)+f(n 2)。

分析到这里，我们也不难看出这实际上就是斐波那契数列了。

---

找规律

找规律最简单的方法就是再写几组，然后观察这些情况下台阶数和走上该台阶的方法数之间的关系。不妨将n取作4，取作6再试一试，用同样的思路计算f(4)和f(6)。

当然，其实在分析的过程中我们就已经发现，走上第n级台阶的方法数，就是第（n-1）阶的方法数+第（n-2）阶的方法数。即使重新举例，也不难发现其中有大量重复的步骤。因此我们可以确定如下规律：

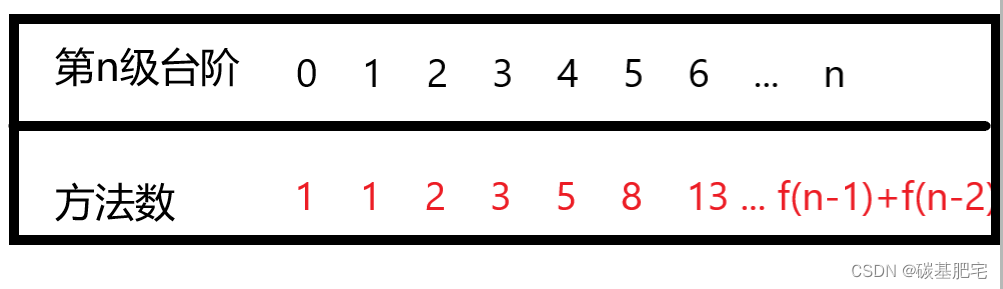
当n>2时，f(n) = f(n-1)+f(n-2)

当n<=2 && n>0时，f(n) = n

当然，根据题意n∈[1,30]，第0级台阶不考虑

2. 代码展示 

#include <stdio.h>

int walk(int n)
{
    if (n <= 2)
        return n;
    else
        return walk(n - 1) + walk(n - 2);
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    int ret = walk(n);
    printf("%d\n", ret);

    return 0;
}

我们经过分析发现，台阶问题的解法确实和斐波那契数列的算法相同。因而也不奇怪为什么台阶问题看似和兔子问题毫无关系，但实质上是同一类问题了。

---

四、拓展用例：矩形覆盖问题

题干如下

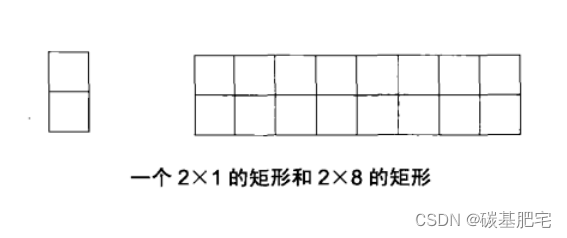
我们可以用 2x1 （下图的左边）的小矩形横着或者竖着去覆盖更大的矩形。

请问用8个 2x1 的小矩形无重叠地覆盖一个 2x8 的大矩形(下图矩形的右边)，总共有多少种方法?

三板斧的使用

举例

本题中不需要特别的去举例，因为题干已经明确了最终的大矩形是由8个小矩形拼成的。换句话说，确定了n = 8.

模拟

这道题我们介绍一种思路。和上面的题目大同小异。

我们先把 2x8 的覆盖方法记为f(8)。

用第一个1x2小矩形去覆盖大矩形的最右边时，有两个选择：竖着放或者横着放。

最简单的情况：1*2的矩形

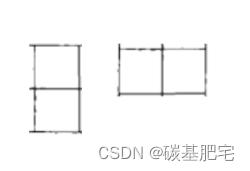
当其中一个竖着放的时候，左边还剩下2x7的区域，这种情形下的覆盖方法记为f(7)。

还留下2*7

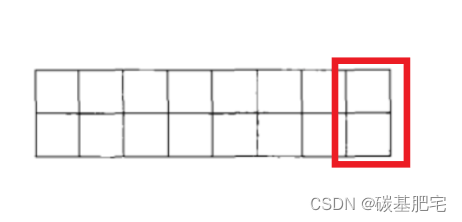
接下来考虑横着放的情况。当1x2的小矩形横着放在右上角的时候，右下角必须和横着放一个1x2的小矩形，而在左边还还剩下2x6的区域，这种情形下的覆盖方法记为f(6)。

还留下2*6

---

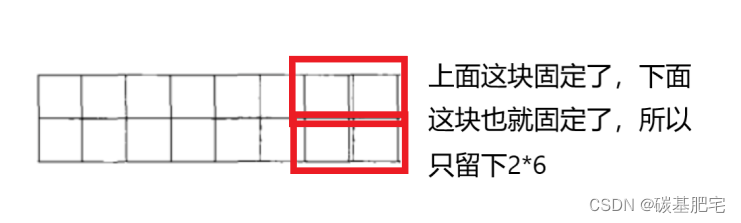
找规律

根据如上模拟，有：f(8)= f(7)+ f(6)，即2*8的矩形覆盖的方法等于2*7的矩形方法 + 2*6的矩形方法。

此时我们可以看出，这仍然是斐波那契数列。 

---

五、总结

1.  牢记题干分析三板斧：举例 + 模拟（画图）+ 找规律。这是一个将抽象的题干转化为具象的功能模型的过程。大家曾经接触过的很多题目，如动态打印菱形、排序问题等，都可以用这样的分析方法解决。而本文以斐波那契数列的相关题目为例，介绍了这个分析方法。
2. 切记死记硬背。第一次遇到问题，分析不准确很正常。在相同的题型归纳总结的过程中，我们要有意识地去提高分析问题的能力，就好比今天的题目种，我们要做的是通过分析，分析出它是斐波那契数列模型，而不是知道一些这是斐波那契数列可以做的，而努力去套。这样容易混乱。
3. 斐波那契数列问题的模拟环节，可以从最简单的情况入手：n为1。虽然在台阶问题种介绍了两种思路，但相比起来，那其中的第二种思路是更通用更好想一些的。倒推的思路在台阶问题中非常容易，在下面的矩形问题中，便不再好用了。
4. 三板斧听着简单，实际上很多人并不熟悉。对于初学者而言，这样培养题感是很不错的，等到熟练起来了，三板斧将会化为“内功”。注意：画图这个环节是非常重要的，不要因为懒或者图省事就直接上手敲。