原文地址:http://m.blog.csdn.net/article/details?id=50492787
一、广告计算的基本概念
1、广告的形式
在互联网发展的过程中,广告成为了互联网企业盈利的一个很重要的部分,根据不同的广告形式,互联网广告可以分为:
- 展示广告(display ads)
- 赞助商搜索广告(sponsored search)
- 上下文广告(contextual advertising)
2、竞价模型
对于在线广告,主要有如下的几种竞价模型:
- 按展示付费(pay-per-impression):直观来讲,按展示付费是指广告商按照广告被展示的次数付费,这是一种最普遍的竞价模型;
- 按行为付费(pay-per-action):按行为付费是指只有在广告产生了销售或者类似的一些转化时,广告商才付费;
当然,对于以上的两种竞价模型各有其局限性:在按展示付费模型中,压根没有考虑到广告的效果,只是按照广告流量进行售卖的模式;对于按行为付费模型,虽然其考虑到了广告效果,但其的条件是产生了某种转化,这种转化有时很难追踪和记录。此时,为了解决这两种模型的局限性,通常可以按照一个用户是否会点击广告作为最终的度量标准,即按点击付费模型(pay-per-click)。
- 按点击付费(pay-per-click):根据用户是否会点击广告来付费。
这里便出现了一个重要的概念,便是广告点击率(the click-through rate, CTR)。
3、广告点击率(CTR)
广告点击率CTR是度量一个用户对于一个广告的行为的最好的度量方法,广告点击率可以定义为:对于一个广告的被点击(click)的次数于被展示(impression)的次数的比值。
广告点击率对于在线广告有着重要的作用,在网络中,对于有限的流量,通常要选择出最优质的广告进行投放,此时,CTR可以作为选择广告和确定广告顺序的一个重要的标准。
但是在计算CTR时,由于数据的稀疏性,利用上述的计算方法得到的CTR通常具有较大的偏差,这样的偏差主要表现在如下的两种情况:
- 1、例如展示impression的次数很小,如 1 次,其中,点击的次数也很小(这里的很小是指数值很小),如 1 ,按照上述的CTR的计算方法,其CTR为 1 ,此时的点击率就被我们估计高了;
- 2、例如展示的次数很大,但是点击的次数很小,此时,利用上述的方法求得的CTR就会比实际的CTR要小得多。
出现上述两种现象的主要原因是我们对分子impression和分母click的估计不准确引起的,部分原因可能是曝光不足等等,对于这样的问题,我们可以通过相关的一些广告的展示和点击数据对CTR的公式进行平滑处理。
二、CTR的平滑方法
1、数据的层次结构——贝叶斯平滑
假设有 N 个相同的账号 (a1,a2,⋯,aN) ,对于网页 p ,对于这样的网页和账号组 (p,ai) 。假设 (C1,C2,⋯,CN) 为观测到点击数据, (r1,r2,⋯,rN) 为隐含的CTR的值,为点击率,点击率在此是一个隐含的参数,广告是否被点击满足二项分布,即 Binomial(Ii,ri) ,其中, Ii 表示广告被展示的次数。
贝叶斯思想认为,隐含的参数不是一个具体的值,而是满足某个分布,我们知道贝叶斯参数估计的基本过程为:
先验分布+数据的知识=后验分布
已知二项分布的共轭分布为Beta分布,对此,有以下的两点假设:
- 1、对于一个广告,其点击 Ci 符合二项分布 Binomial(Ii,ri) ,其中, Ii 表示的是展示的次数, ri 表示的是广告被点击的概率;
- 2、对于所有的广告,有其自身的CTR,其CTR满足参数是 α 和 β 的贝塔分布 Beta(α,β) 。
假设有 N 个广告,广告被展示的次数为 (I1,I2,⋯,IN) ,广告被点击的次数为 (C1,C2,⋯,CN) ,上述的两个假设可以表示为如下的形式:
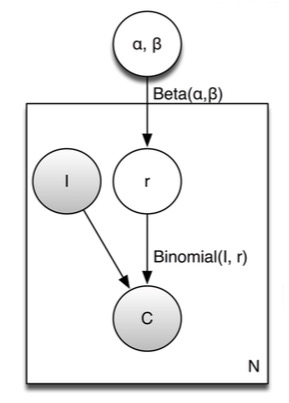
其对应的概率图模型为:
点击率 ri 不仅与 (Ii,Ci) 相关,而且与参数 α 和参数 β 相关,我们可以通过计算得到参数 α 和参数 β 的估计 α̂ 和 β̂ ,一旦 α̂ 和 β̂ 被确定后,则 ri 的估计为:
所以,现在,我们需要求解参数 α 和参数 β 的估计 α̂ 和 β̂ 。
点击 C 的似然函数为: ℙ(C1,C2,⋯,CN∣I1,I2,⋯,IN,α,β) ,由于点击的次数以及展示的次数之间都是相互独立的,因此上式可以表示为:
已知
则上式可以写成:
此时,我们需要求得该似然函数的最大值,首先,我们对上述的似然函数取对数,即为:
将上述的log似然函数分别对 α 和 β 求导数,即为:
其中,
Ψ(x)=ddxlnΓ(x)
。通过the fixed-point iteration方法,可以得到如下的结果:
上述的求解过程是一个迭代的过程,一旦求出了参数 α 和参数 β 的估计 α̂ 和 β̂ ,便可以求出点击率的估计:
2、数据在时间上的一致性——指数平滑
相比上述的贝叶斯平滑,指数平滑相对要简单点,对于CTR中的点击,这是个与时间相关的量,假设对于一个广告,有 M 天的点击和展示数据 (I1,I2,⋯,IM) , (C1,C2,⋯,CM) 。若要估计第 M 天的CTR的值,我们需要对分别对 I 和 C 进行平滑,得到平滑后的 Î 和 Ĉ 。其计算方法如下:
其中, γ 称为平滑因子,且 0<γ<1 。对于上述的公式,若要计算第 M 天的平滑点击,可以得到下面的公式:
参考文献
- Click-Through Rate Estimation for Rare Events in Online Advertising.Xuerui Wang, Wei Li, Ying Cui, Ruofei (Bruce) Zhang, Jianchang Mao Yahoo! Labs, Silicon Valley United States










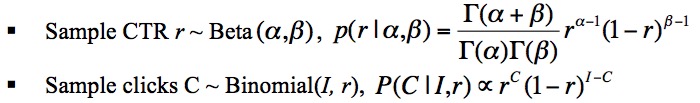














 695
695

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








