决策树

决策树

决策树的基本思想很简单：就是按照不同的属性值，将所有样本进行决策，然后再在各个子样本中按照新的属性再次进行决策，重复进行，知道所有的样本都做出了最终决策。

一般情况下，一棵决策树包含一个根结点和若干个内部结点和若干个叶子结点；叶子结点表示的是决策结果，其他结点对应的是属性值测试。每个结点都包含了一定的样本，树的同一层所有结点包含的样本总和就是训练样本。

算法伪代码

常见问题

1、如何选择最优划分属性？也就是如何确定每一次该选择哪种属性来做决策。

<基于信息增益的选择>

在划分的过程中，希望决策树的分支结点所包含的样本尽可能的属于同一类别，或者说希望各个结点的纯度要高一些，最好不要各个类别都有。对于纯度的描述，最好的可以借鉴信息学中的熵的概念来描述，熵描述的是混乱的程度，熵大越混乱，熵小越规则整齐。信息熵定义为：

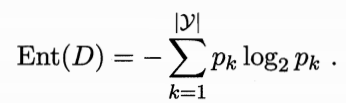
对于某个属性，它能有不同的取值，每种取值，在划分过程中对应一个结点，那么这个结点在划分过程中就能可以计算信息熵，而对于该属性，我们则可以定义信息增益来描述该属性的影响程度：

定义信息熵和信息增益后，我们就能通过信息增益的大小来选择下一步使用的最优属性，信息增益越大，意味着该属性影响程度越大，反之越小。这种选择方式是 ID3决策树算法中使用的属性选择规则。

<基于信息增益率的选择>

但是，属性取值数目的多少对信息增益的影响很大，为减少这种影响，可以定义增益率来选择划分属性。著名的C4.5决策树算法就是通过这种方式选择划分属性。增益率定义如下：

<基于基尼系数的选择>

CART（classfication and regression tree）决策树使用的基尼系数来进行划分属性的选择。基尼值表示结点的纯度，基尼值越小纯度越高，定义如下：

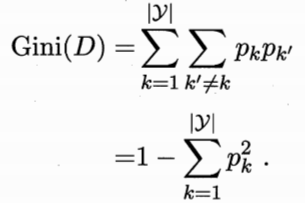
属性的基尼系数定义如下，选择基尼系数最小的属性做为最优划分属性。

2、训练过程中如何防止过拟合？

剪枝是决策树中防止过拟合的主要方法。大致分为预剪枝和后剪枝两种。预剪枝是在决策树的生成过程中，对每个结点在划分前进行估计，若当前结点的划分不能带来决策树泛华能力的提升时则停止划分并将当前结点标记为叶子结点。后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶子结点进行考察，若将该结点对应的子树替换为叶结点能否提升泛化能力则进行替换。

3、如何判断决策树的泛化能力是否得到提升？

使用验证集对其进行测试。

4、如果属性值是连续的怎么办？

此时可以采用连续属性离散化的技术，简单的策略就是二分法。将连续属性出现的样本对应的值按升序排列，然后先去相邻两个值之间的重点作为一个离散点进行划分。

5、如果样本的属性值确实了如何处理？

1）在选择划分属性的时候，可以使用那个属性值完整的样本进行选择。

2）为每一个样本定义一个权重，若样本在该属性处未发生缺失，则按照相应的属性值进入下一个子结点，权重不发生改变；如果发生缺失，则划入所有的子结点，并更新其权重。

多变量决策树