第三章常见模型统计参数的后验分布
2.设某校学生的身高(单位:cm)服从N(θ,25),今从该校学生中随机抽取10人测量其身高,其平均高度为 175.34cm,设平均高度θ的先验分布为N(172.72,2.56),求θ的后验分布.

4.设X1,…,Xn为从正态总体N(θ,4)中抽取的随机样本,又设θ的先验分布为正态分布。
(1)若样本容量n=100,证明:不管先验标准差为多少,后验标准差一定小1/5.
(2)若θ的先验分布的标准差为1,要使后验方差不超过0.1,最少要抽取样本容量多大的样本?

8.从一批产品中抽检100个,发现3个不合格品,假定该产品不合格率θ的先验分布为贝塔分布Be(2,200),求θ的后验分布.

12.设X=(X1,…,Xn)是从负二项分布Nb(r,θ)中抽取的随机样本,θ的先验分布是贝塔分布Be(α,β),其中α和β已知.证明:给定x的条件下,θ的后验分布为Be(α+rn,x1+x2+…+xn-nr+β)

14,设θ表示每100米长磁带上缺陷数的平均数,检查1200米长这类磁带,发现4个缺陷.令θ的先验分布服从伽玛分布,均值和方差分别为1和3,求θ的后验分布。

16.设随机变量X服从指数分布Exp(λ),其密度函数为
p(x|λ)=λexp{-λx}(x).令X1,…,Xn是从上述指数分布中抽取的随机样本,假定λ的先验分布是伽玛分布,其均值为0.0002,先验标准差为0.0001.
(1)确定先验分布中的超参数;
(2)求λ的后验分布.
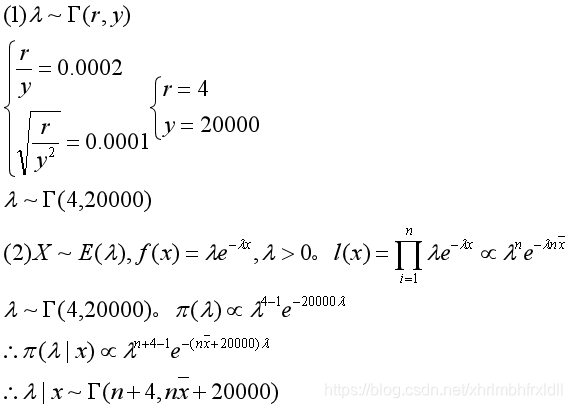








 本文探讨了统计学中的后验分布概念,通过多个实例展示了如何计算不同模型参数的后验分布。其中包括正态分布、负二项分布和伽玛分布等,涉及贝塔分布作为先验的知识,并讨论了样本容量对后验分布方差的影响。此外,还涵盖了指数分布和伽玛分布的后验分布问题,以及在实际应用中如何确定先验分布的超参数。
本文探讨了统计学中的后验分布概念,通过多个实例展示了如何计算不同模型参数的后验分布。其中包括正态分布、负二项分布和伽玛分布等,涉及贝塔分布作为先验的知识,并讨论了样本容量对后验分布方差的影响。此外,还涵盖了指数分布和伽玛分布的后验分布问题,以及在实际应用中如何确定先验分布的超参数。
















 4162
4162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








