蓝桥之手撕排序算法——冒泡、选择、插入、快排、归并(Python版)

目录

1. 排序引言

2. 冒泡排序

2.1 算法思想

2.2 代码实现

 2.3 时空复杂度分析

3. 选择排序

3.1 算法思想

3.2 代码实现

 3.3 时空复杂度分析

4. 插入排序

4.1 算法思想

4.3 代码实现

4.4 时空复杂度分析

5. 快速排序

5.1 算法思想

5.2 代码实现

5.3 时空复杂度分析

6. 归并排序

6.1 算法思想

6.2 代码实现

6.3 时空复杂度分析

---

1. 排序引言

排序算法是算法竞赛中的第一入门必会的算法，可能在语言里面内置好sort排序函数，但是在排序算法中的很多思想是值得我们去学习的，比如从快速排序里面学会如何进行分治以及递归的实现。

2. 冒泡排序

冒泡排序是学习语言和算法中必会的一种算法，下面就由我来进行冒泡排序的分析与代码实现：

2.1 算法思想

对于一个无序数组，我们从索引0开始往右对比，如果当前数字比后一个数字大，就进行交换。

这样每次就可以将最大的放在最右边， 上一次对比的最右边的就不再参与下一次排序

因为有N个数，每一次可以将一个最大数排好序，最后一个数也就定好了，因此只需要N-1次，就能排好完整的序。

我们可以看看以下的图：

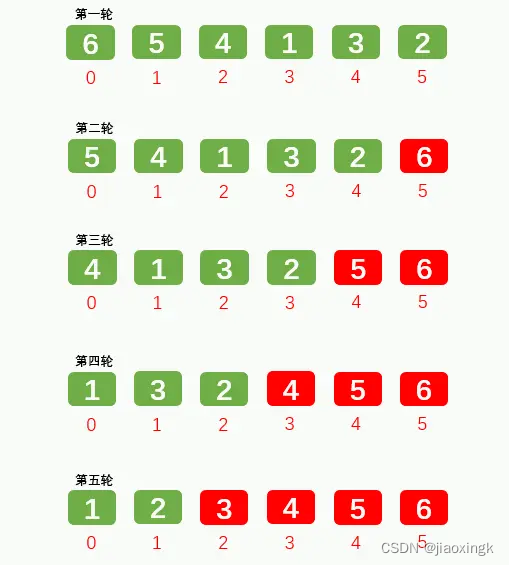
其实到这里，冒泡排序算法就已经很明确了，每次冒泡都能求出当前最大的数，并将其放在最右边。

2.2 代码实现

a = [6, 5, 4, 1, 3, 2]
n = len(a)
for i in range(n - 1):
    for j in range(n - i - 1):
        if a[j] > a[j + 1]:
            a[j], a[j + 1] = a[j + 1], a[j]
print(a)

 2.3 时空复杂度分析

时间复杂度：

        每次需要比较进行n - i - 1次，也就是n - 1 、 n - 2 、 n - 3.....1次

        一共要执行n - 1次， 大概估算也就是O（n²）

空间复杂度：

        在原数组上面进行的操作，并没有开辟新的空间，所以为：O(1)

3. 选择排序

3.1 算法思想

每次从左往右开始找，找到最小的，然后与当前的索引的数进行交换，并索引加一

这样就能保证，每次都将最小的数排在最前面了。

3.2 代码实现

a = [6, 5, 4, 1, 3, 2]
n = len(a)
for i in range(n - 1):
    minn = a[i]
    index = i
    for j in range(i + 1, n):
        if a[j] < minn:
            minn = min(minn, a[j])
            index = j

    a[i], a[index] = a[index], a[i]
print(a)