四、空间解析几何（高数）

文章仅作学习记录使用

四、空间解析几何（高数）

1.向量代数

既有大小又有方向的量称为向量。
设a$=(a_x,a_y,a_z)$,b$=(b_x,b_y,b_z)$,c$=(c_x,c_y,c_z)$,a,b,c均不是零向量。
数学上研究的是自由向量，其特点是与起点无关，简称为大家所熟悉的“向量”。
方向角与方向余弦
非零向量$\mathbf{a}$与三条坐标轴的夹角$\alpha ,\beta ,\gamma$称为$\mathbf{r}$的方向角。设$\mathbf{a}=(x,y,z)$则，$$\begin{gathered} \cos \alpha =\frac{x}{|\mathbf{a}|}，\cos \beta =\frac{y}{|\mathbf{a}|}，\cos \gamma =\frac{z}{|\mathbf{a}|} \\ \cos {\alpha }^2+\cos {\beta }^2+\cos {\gamma }^2=1 \\ (\cos \alpha ,\cos \beta ,\cos \gamma )=\frac{\vec{a}}{|\vec{a}|}={\mathbf{a}}^0 \end{gathered}$$${\mathbf{a}}^0$即表示与$\vec{a}$同方向的单位向量。

（1）数量积

$$\mathbf{a}\cdot \mathbf{b}=(a_x,a_y,a_z)\cdot (b_x,b_y,b_z)=a_x{b}_x+a_y{b}_y+a_z{b}_z\text{\hspace{1em}(4.1)}$$
$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos \theta =\frac{\mathbf{a}\cdot \mathbf{b}}{|\vec{a}||\vec{b}|}=\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{\sqrt{a_x^2+a_y^2+a_z^2}+\sqrt{b_x^2+b_y^2+b_z^2}}\text{\hspace{1em}(4.2)}$$公式4.2为数量积的定义式，$\theta$为$\mathbf{a},\mathbf{b}$的夹角。
垂直$a\cdot b=0$
$$\mathbf{a}\perp \mathbf{b}\iff \theta =\frac{\pi }{2}\iff |\vec{a}||\vec{b}|\cos \theta =0\iff a_x{b}_x+a_y{b}_y+a_z{b}_z=0\text{\hspace{1em}(4.3)}$$
投影
$$Pr{j}_{b}a=\frac{\vec{a}\cdot \vec{b}}{|\vec{b}|}=\frac{\vec{a}\cdot \vec{b}}{|\vec{a}||\vec{b}|}=\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{\sqrt{b_x^2+b_y^2+b_z^2}}\text{\hspace{1em}(4.4)}$$称为a在b上的投影。

（2）向量积

$$\mathbf{a}\times \mathbf{b}=\left(\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right)\text{\hspace{1em}(4.5)}$$其中$|\mathbf{a}\times \mathbf{b}|=|\mathbf{a}||\mathbf{b}|\sin \theta$,用右手规则确定方向（转向角不超过$\pi$),$\theta$为$\mathbf{a},\mathbf{b}$的夹角。

平行$\mathbf{a}\times \mathbf{b}=0$

$\mathbf{a}//\mathbf{b}\iff \theta =0或\pi \iff \frac{a_x}{b_x}=\frac{a_y}{b_y}=\frac{a_z}{b_z}$

（3）混合积

①公式：$[\mathbf{abc}]=(\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}=\left|\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}\right|$

②三向量共面$⟺\left|\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}\right|=0$

③根据行列式性质2
互换行列式的两行（或列），行列式变号。
3个向量进行混合积运算，其行列式的三行即为3个向量的坐标（x,y,z）,不同只在于3个向量所在位置不同，换行两次即可实现完全相同，故可以推断出以下公式：
  $(\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}=(\mathbf{b}\times \mathbf{c})\cdot \mathbf{a}$
同样的还有：
  $(\mathbf{c}\times \mathbf{a})\cdot \mathbf{b}=(\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}$

（4）向量的方向角和方向余弦

（1）$\vec{a}$与x轴、y轴、z轴的正向的夹角$\alpha 、\beta 、\gamma$称为$\vec{a}$的方向角。

（2）$\cos \alpha 、\cos \beta 、\cos \gamma$称为$\vec{a}$的方向余弦，且$\cos \alpha =\frac{a_x}{\mathbf{a}},\cos \beta =\frac{a_y}{\mathbf{a}},\cos \gamma =\frac{a_z}{\mathbf{a}}$。

（3）${\mathbf{a}}^0=\frac{\mathbf{a}}{|\mathbf{a}|}=(\cos \alpha ,\cos \beta ,\cos \gamma )$称为向量$\vec{a}$的单位向量（表示方向的向量）。

（4）任意向量$\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}=(r\cos \alpha ,r\cos \beta ,r\cos \gamma )=r(\cos \alpha ,\cos \beta ,\cos \gamma )$，其中$\cos \alpha ,\cos \beta ,\cos \gamma$为$\mathbf{r}$的方向余弦，r为$\mathbf{r}$的模，$\cos \alpha =\frac{x}{\sqrt{x^2+y^2+z^2}},\cos \beta =\frac{y}{\sqrt{x^2+y^2+z^2}},\cos \gamma =\frac{z}{\sqrt{x^2+y^2+z^2}},\mathbf{r}=\sqrt{x^2+y^2+z^2}$。

---

2.空间平面与直线

（1）平面方程

以下假设平面的法向量$\mathbf{n}=(A,B,C)$，平面的方程为以下四种：
①一般式：$Ax+By+Cz+D=0$

②点法式：$A(x-x_0)+B(y-y_0)+C(z-z_0)=0$

③三点式:$\left|\begin{array}{ccc}x-x_1& y-y_1& z-z_1\\ x-x_2& y-y_2& z-z_2\\ x-x_3& y-y_3& z-z_3\end{array}\right|=0$(平面过不共线的三点$\mathbf{P}(x_i,y_i,z_i),i=1,2,3$)

注释：设$P(x,y,z)$为平面$\pi$上任一点，则$\overrightarrow{P{P}_1},\overrightarrow{P{P}_2},\overrightarrow{P{P}_3},$三个向量共面，则其混合积$(\overrightarrow{P{P}_1}\times \overrightarrow{P{P}_2})\cdot \overrightarrow{P{P}_3}=0,$可得三点式平面方程。

④截距式：$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$（平面过$(a,0,0),(0,b,0),(0,0,c)$三点）

⑤平面族方程
通过直线$l:\{\begin{array}{l}{A}_{1}x+B_{1}y+C_{1}z+D_1=0,\\ A_{2}x+B_{2}y+C_{2}z+D_2=0\end{array}$的平面族方程为$A_{1}x+B_{1}y+C_{1}z+D_1+\lambda (A_{2}x+B_{2}y+C_{2}z+D_2)=0$其中平面$A_{2}x+B_{2}y+C_{2}z+D_2=0$不在平面族方程内。

（2）直线方程

以下假设直线的方向向量$\tau =(l,m,n)$。

①一般式：$\{\begin{array}{l}{A}_{1}x+B_{1}y+C_{1}z+D_1=0,{\mathbf{n}}_1=(A_1,B_1,C_1),\\ A_{2}x+B_{2}y+C_{2}z+D_2=0,{\mathbf{n}}_2=(A_2,B_2,C_2),\end{array}$其中${\mathbf{n}}_1$不平行于${\mathbf{n}}_2$。
(一般式是由两个平面相交产生的直线，两个等式分别对应两个平面公式)

②点向式：$\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}$

③参数式：$\{\begin{array}{l}x=x_0+lt\\ y=y_0+mt\\ z=z_0+nt\end{array}$,$M(x_0,y_0,z_0)$为直线上的已知点，$t$为参数。

④两点式：$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$（直线过不同的两点${\mathbf{P}}_i(x_i,y_i,z_i),i=1,2$）

（3）位置关系

距离
点$\mathbf{P}$到平面$Ax+By+Cz+D=0$的距离$d=\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}$。

直线间的关系
设${\tau }_1=(l_1,m_1,n_1),{\tau }_2=(l_2,m_2,n_2)$分别为直线$L_1,L_2$的方向向量。

$$\begin{gathered} 垂直：L_1\perp L_2\iff {\tau }_1\perp {\tau }_2\iff l_1{l}_2+m_1{m}_2+n_1{n}_2=0 \\ 平行：L_1\parallel L_2\iff {\tau }_1\parallel {\tau }_2\iff \frac{l_1}{l_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2} \end{gathered}$$

平面间的关系
设平面${\pi }_1,{\pi }_2$的法向量分别为${\mathbf{n}}_1=(A_1,B_1,C_1),{\mathbf{n}}_2=(A_2,B_2,C_2)$

$$\begin{gathered} 垂直：{\pi }_1\perp {\pi }_2\iff {\mathbf{n}}_1\perp {\mathbf{n}}_2\iff A_1{A}_2+B_1{B}_2+C_1{C}_2=0 \\ 平行：{\pi }_1\parallel {\pi }_2\iff {\mathbf{n}}_1\parallel {\mathbf{n}}_2\iff \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} \end{gathered}$$

平面与直线的关系
设直线$L$的方向向量为$\tau =(l,m,n)$,平面的法向量为$\mathbf{n}=(A,B,C)$

$$\begin{gathered} 垂直：L\perp \pi \iff \tau \parallel \mathbf{n}\iff \frac{A}{l}=\frac{B}{m}=\frac{C}{n} \\ 平行：L\parallel \pi \iff \tau \perp \mathbf{n}\iff Al+Bm+Cn=0 \end{gathered}$$

$线线①、面面②的位置公式一一对应，而线面③的位置公式互相反转，仅记住相反的③即可。$

---

3.空间曲线与曲面

（1）空间曲线

①一般式：$\Gamma :\{\begin{array}{l}F(x,y,z)=0\\ G(x,y,z)=0\end{array}$其几何背景为两个曲面的交线。

②参数方程：$\Gamma :\{\begin{array}{l}x=\phi (t),\\ y=\psi (t),\\ z=\omega (t),\end{array}t\in [\alpha ,\beta ]$

③空间曲线在坐标面上的投影
以求曲线$\Gamma$在平面上的投影曲线为例：
将$\Gamma :\{\begin{array}{l}F(x,y,z)=0\\ G(x,y,z)=0\end{array}$中的$z$消去，得到$\phi (x,y)=0$,
则曲线$\Gamma$在$xOy$面上的投影曲线包含于曲线$\{\begin{array}{l}\phi (x,y)=0.\\ z=0.\end{array}$

曲线$\Gamma$在其他平面上的投影曲线可类似求得。

（2）空间曲面

（1）曲面方程：$F(x,y,z)=0$
（2）二次曲面


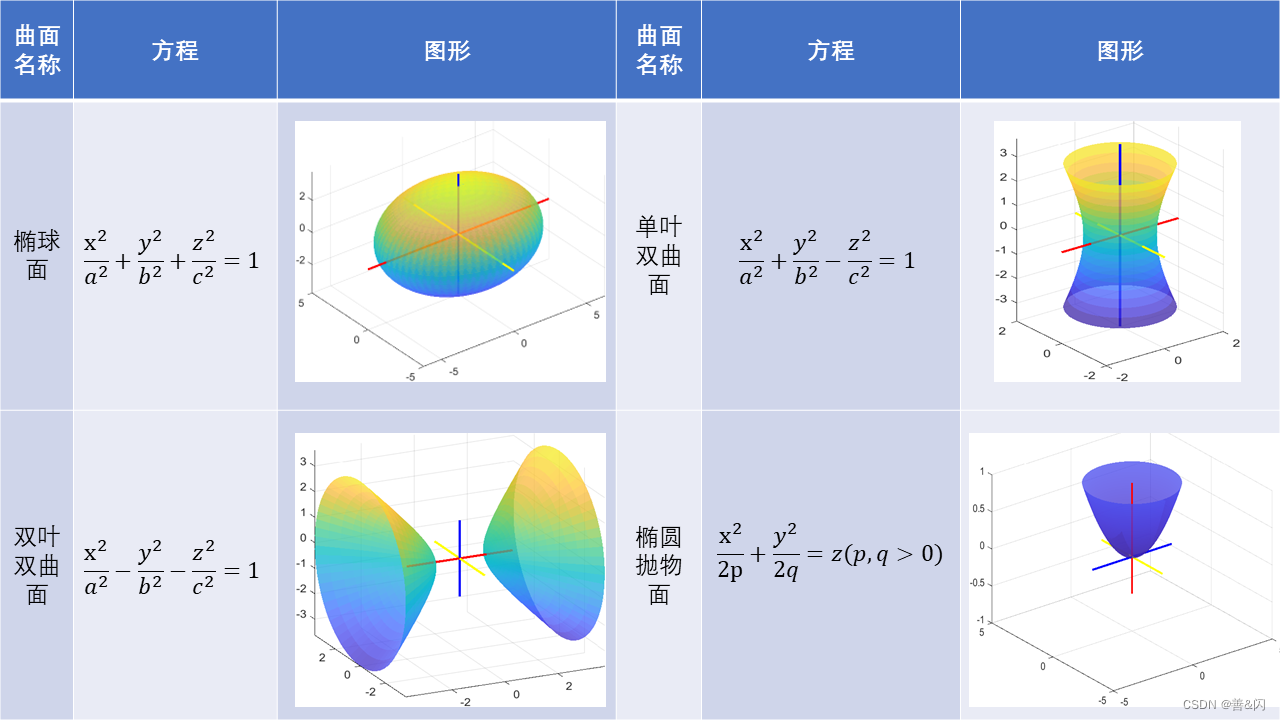
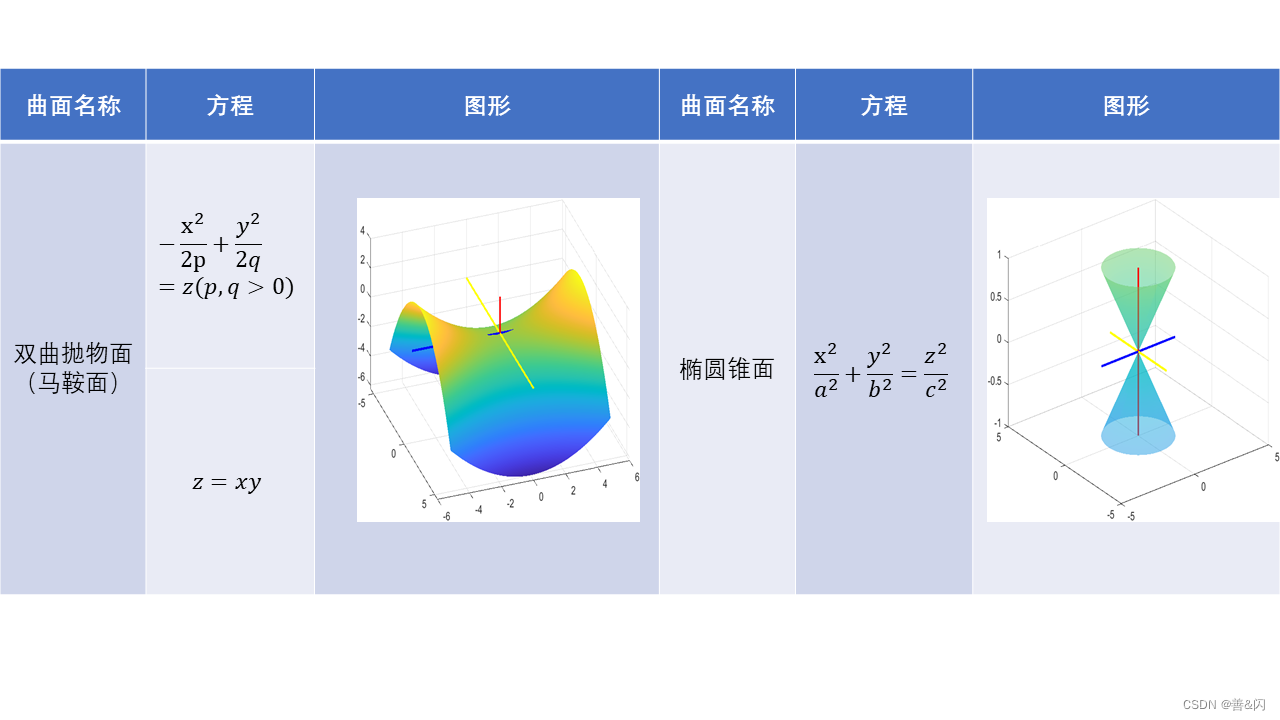
（3）柱面：动直线沿定曲线平行移动所形成的曲面

椭圆柱面 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

双曲柱面 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

抛物柱面 $y=a{x}^2$
注：在空间解析几何中，一般认为缺少变量的方程为柱面。
（4）旋转曲面（重点）：曲线$\Gamma$绕一条定直线旋转一周所形成的曲面。
曲线$\Gamma :\{\begin{array}{l}F(x,y,z)=0,\\ G(x,y,z)=0\end{array}$绕直线$L:\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}$旋转形成一个曲面，旋转曲面的求法如下：

如图所示，已知$M_0(x_0,y_0,z_0)$，方向向量$\vec{s}=(m,n,p).$在母线$\Gamma$上任取一点$M_1(x_1,y_1,z_1)$，则过$M_1$的维圆上的任意一点$P(x,y,z)$满足条件$\overrightarrow{M_{1}P}\perp \mathbf{s},|\overrightarrow{M_{1}P}|=|\overrightarrow{M_0{M}_1}|$,即$\{\begin{array}{l}m(x-x_1)+n(y-y_1)+p(z-z_1)=0\\ (x-x_0{)}^2+(y-y_0{)}^2+(z-z_0{)}^2=(x_1-x_0{)}^2+(y_1-y_0{)}^2+(z_1-z_0{)}^2,\end{array}$与方程$F(x_1,y_1,z_1)=0$和$G(x_1,y_1,z_1)=0$联立消去$x_1,y_1,z_1,$便可得到旋转曲面的方程。

---

4.多元函数微分学的几何应用

（1）空间曲线的切线与法平面

（1）设空间曲线$\Gamma$由参数方程$\{\begin{array}{l}x=\phi (t),\\ y=\psi (t),\\ z=\omega (t)\end{array}$给出，其中$\phi (t),\psi (t),\omega (t)$均可导，

$P_0(x_0,y_0,z_0)$是$\Gamma$上的点，且当$t=t_0$时，${\phi }^{{}^{\prime }}(t_0),{\psi }^{{}^{\prime }}(t_0),{\omega }^{{}^{\prime }}(t_0)$都不为0，则

①曲线$\Gamma$在点$P_0(x_0,y_0,z_0)$处的切向量为$\tau =({\phi }^{{}^{\prime }}(t_0),{\psi }^{{}^{\prime }}(t_0),{\omega }^{{}^{\prime }}(t_0))$.

②曲线$\Gamma$在点$P_0(x_0,y_0,z_0)$处的切线方程为$\frac{x-x_0}{{\phi }^{{}^{\prime }}(t_0)}=\frac{y-y_0}{{\psi }^{{}^{\prime }}(t_0)}=\frac{z-z_0}{{\omega }^{{}^{\prime }}(t_0)}$.

③曲线$\Gamma$在点$P_0(x_0,y_0,z_0)$处的法平面（过点$P_0(x_0,y_0,z_0)$且与切线垂直的平面）方程为${\psi }^{{}^{\prime }}(t_0)(x-x_0)+{\phi }^{{}^{\prime }}(t_0)(y-y_0)+{\omega }^{{}^{\prime }}(t_0)(z-z_0)=0$

（2）设空间曲线$\Gamma$由交面式方程$\{\begin{array}{l}F(x,y,z)=0,\\ G(x,y,z)=0\end{array}$给出，则在以下表达式有意义的条件下，有

①曲线$\Gamma$在点$P_0(x_0,y_0,z_0)$处的切向量为
$$\tau =({\left|\begin{array}{cc}{F}_y^{{}^{\prime }}& F_z^{{}^{\prime }}\\ G_y^{{}^{\prime }}& G_z^{{}^{\prime }}\end{array}\right|}_{P_0},{\left|\begin{array}{cc}{F}_z^{{}^{\prime }}& F_x^{{}^{\prime }}\\ G_z^{{}^{\prime }}& G_x^{{}^{\prime }}\end{array}\right|}_{P_0},{\left|\begin{array}{cc}{F}_x^{{}^{\prime }}& F_y^{{}^{\prime }}\\ G_x^{{}^{\prime }}& G_y^{{}^{\prime }}\end{array}\right|}_{P_0}).\text{\hspace{1em}(4.19)}$$②曲线$\Gamma$在点$P_0(x_0,y_0,z_0)$处的切线方程为$$\frac{x-x_0}{{\left|\begin{array}{cc}{F}_y^{{}^{\prime }}& F_z^{{}^{\prime }}\\ G_y^{{}^{\prime }}& G_z^{{}^{\prime }}\end{array}\right|}_{P_0}}=\frac{y-y_0}{{\left|\begin{array}{cc}{F}_z^{{}^{\prime }}& F_x^{{}^{\prime }}\\ G_z^{{}^{\prime }}& G_x^{{}^{\prime }}\end{array}\right|}_{P_0}}=\frac{z-z_0}{{\left|\begin{array}{cc}{F}_x^{{}^{\prime }}& F_y^{{}^{\prime }}\\ G_x^{{}^{\prime }}& G_y^{{}^{\prime }}\end{array}\right|}_{P_0}}.\text{\hspace{1em}(4.20)}$$③曲线$\Gamma$在点$P_0(x_0,y_0,z_0)$处的法平面方程为$${\left|\begin{array}{cc}{F}_y^{{}^{\prime }}& F_z^{{}^{\prime }}\\ G_y^{{}^{\prime }}& G_z^{{}^{\prime }}\end{array}\right|}_{P_0}（x-x_0）+{\left|\begin{array}{cc}{F}_y^{{}^{\prime }}& F_z^{{}^{\prime }}\\ G_y^{{}^{\prime }}& G_z^{{}^{\prime }}\end{array}\right|}_{P_0}（y-y_0）+{\left|\begin{array}{cc}{F}_x^{{}^{\prime }}& F_y^{{}^{\prime }}\\ G_x^{{}^{\prime }}& G_y^{{}^{\prime }}\end{array}\right|}_{P_0}(z-z_0)=0\text{\hspace{1em}(4.21)}$$

（2）空间曲面的切平面与法线

（1）设空间曲面$\Sigma$由方程$F(x,y,z)=0$给出，$P_0(x_0,y_0,z_0)$是$\Sigma$上的点，则

①曲面$\Sigma$在点$P_0(x_0,y_0,z_0)$处的法向量（垂直于该点切平面的向量）为
$\mathbf{n}=(F_x^{{}^{\prime }}(x_0,y_0,z_0),F_y^{{}^{\prime }}(x_0,y_0,z_0),F_z^{{}^{\prime }}(x_0,y_0,z_0)),$且法线方程为$$\frac{x-x_0}{F_x^{{}^{\prime }}(x_0,y_0,z_0)}=\frac{y-y_0}{F_y^{{}^{\prime }}(x_0,y_0,z_0)}=\frac{z-z_0}{F_z^{{}^{\prime }}(x_0,y_0,z_0)}.$$

②曲面$\Sigma$在点$P_0(x_0,y_0,z_0)$处的切平面方程为$$F_x^{{}^{\prime }}(x_0,y_0,z_0)(x-x_0)+F_y^{{}^{\prime }}(x_0,y_0,z_0)(y-y_0)+F_z^{{}^{\prime }}(x_0,y_0,z_0)(z-z_0)=0$$

（2）设空间曲面$\Sigma$由方程$z=f(x,y)$给出，令$F(x,y,z)=f(x,y)-z$，则

①曲面$\Sigma$在点$P_0(x_0,y_0,z_0)$处的法向量为$\mathbf{n}=(f_x^{{}^{\prime }}(x_0,y_0),f_y^{{}^{\prime }}(x_0,y_0),-1),$且法线方程为$$\frac{x-x_0}{f_x^{{}^{\prime }}(x_0,y_0)}=\frac{y-y_0}{f_y^{{}^{\prime }}(x_0,y_0)}=\frac{z-z_0}{-1}$$

②曲线$\Sigma$在点$P_0(x_0,y_0,y_0)$处的平面方程为$$f_x^{{}^{\prime }}(x_0,y_0)(x-x_0)+f_y^{{}^{\prime }}(x_0,y_0)(y-y_0)-(z-z_0)=0$$【注】若用$\alpha ,\beta ,\gamma$表示曲面$z=f(x,y)$在点$P_0(x_0,y_0,z_0)$处的法向量的方向角，并假定法向量的方向是向上的，即它与$z$轴正向所成的角$\gamma$是锐角，则法向量的方向余弦为
$$\cos \alpha =\frac{-f_x}{\sqrt{1+f_x^2+f_y^2}},\cos \beta =\frac{-f_y}{\sqrt{1+f_x^2+f_y^2}},\cos \gamma =\frac{-1}{\sqrt{1+f_x^2+f_y^2}}.$$

---

5.场论初步

（1）方向导数

偏导数反映函数沿着坐标轴方向的变化率，不够全面，需要研究函数沿任一指定方向的变化率，即方向导数。

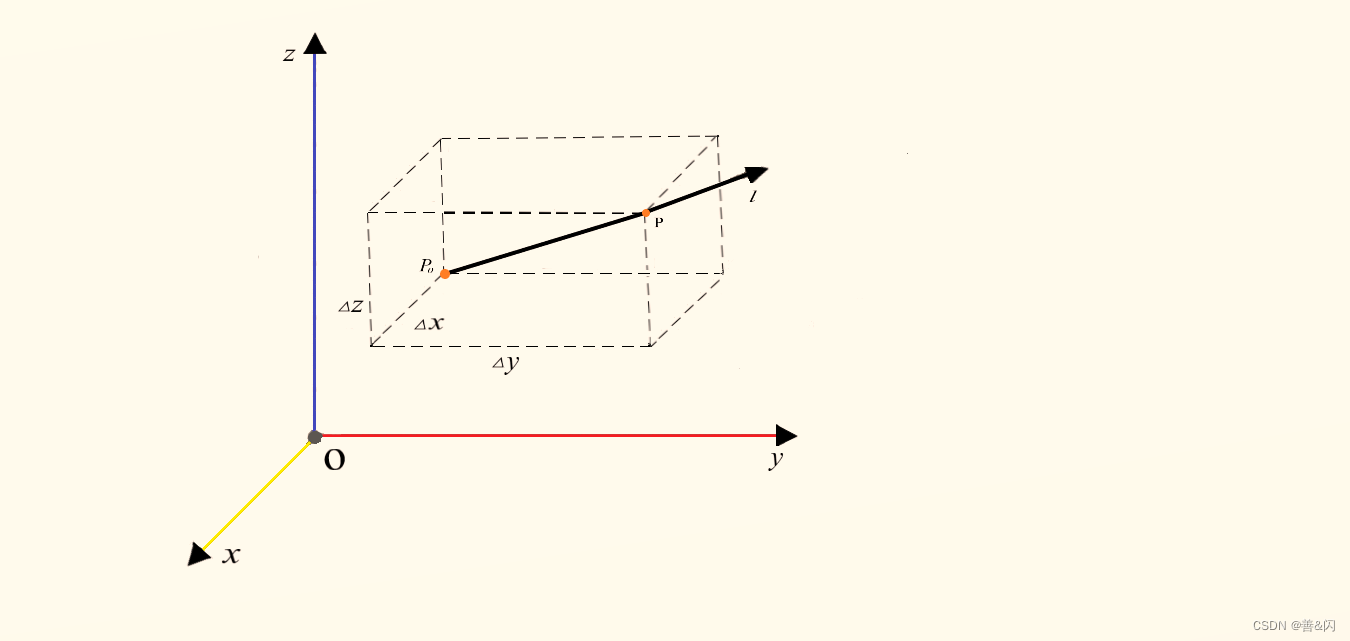
定义1 设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,y_0)$的某空间邻域$U\subset {\mathbf{R}}^3$内有定义，$l$为从点$P_0$出发的射线，$P(x,y,z)$为$l$上且在$U$内的任一点，则$$\{\begin{array}{l}x-x_0=\Delta x=t\cos \alpha ,\\ y-y_0=\Delta y=t\cos \beta ,\\ z-z_0=\Delta z=t\cos \gamma .\end{array}$$以$t=\sqrt{(\Delta x{)}^2+\Delta y{)}^2+\Delta z{)}^2}$表示$P$与$P_0$之间的距离，如图所示，若极限
$$\underset{t\to 0^{+}}{\lim }\frac{u(P)-u(P_0)}{t}=\underset{t\to 0^{+}}{\lim }\frac{u(x_0+t\cos \alpha ,y_0+t\cos \beta ,z_0+t\cos \gamma )-u(x_0,y_0,z_0)}{t}$$存在，则称此极限为函数$u=u(x,y,z)$在点$P_0$沿方向$l$的方向导数，记作${\frac{\partial u}{\partial \mathbf{l}}|}_{P_0}.$

定理（方向导数的计算公式） 设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,y_0)$处可微分，则$u=(x,y,z)$在点$P_0$处沿任一方向$l$的方向导数都存在，且
$${\frac{\partial u}{\partial \mathbf{l}}|}_{P_0}=u_x^{{}^{\prime }}(P_0)\cos \alpha +u_y^{{}^{\prime }}(P_0)\cos \beta +u_z^{{}^{\prime }}(P_0)\cos \gamma \text{\hspace{1em}(4.27)}$$其中，$\cos \alpha ,\cos \beta ,\cos \gamma$为$l$的方向余弦。

（2）梯度

定义2 设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,y_0)$处有一阶偏导数，则定义$${\mathbf{grad}\mathbf{u}|}_{P_0}=(u_x^{{}^{\prime }}(P_0),u_y^{{}^{\prime }}(P_0),u_z^{{}^{\prime }}(P_0))$$为函数$u=u(x,y,z)$在点$P_0$处的梯度。

（3）方向导数与梯度的关系

由方向导数的计算公式4.27与梯度定义可得$$\begin{array}{rl}{\frac{\partial u}{\partial \mathbf{l}}|}_{P_0}& =(u_x^{{}^{\prime }}(P_0)+u_y^{{}^{\prime }}(P_0)+u_z^{{}^{\prime }}(P_0))\cdot (\cos \alpha ,\cos \beta ,\cos \gamma )\\ & ={\mathbf{grad}u|}_{P_0}\cdot {\mathbf{l}}^0\\ & =|{\mathbf{grad}u|}_{P_0}||{\mathbf{l}}^0|\cos \theta \\ & =|{\mathbf{grad}u|}_{P_0}|\cos \theta \end{array}$$其中$\theta$为${\mathbf{grad}u|}_{P_0}与{\mathbf{l}}^0$的夹角，当$\cos \theta =1$时，${\frac{\partial u}{\partial \mathbf{l}}|}_{P_0}$有最大值。

结论 函数在某点的梯度是一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。

（4）散度与旋度

设向量场$\mathbf{A}(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z)),$即$\vec{A}=\mathbf{P}\vec{i}+\mathbf{Q}\vec{j}+\mathbf{R}\vec{k}$则散度$$divA=\frac{\partial \mathbf{P}}{\partial x}+\frac{\partial \mathbf{Q}}{\partial y}+\frac{\partial \mathbf{R}}{\partial z},$$旋度$$\mathbf{rot}A=\begin{array}{cccc}& \mathbf{i}& \mathbf{j}& \mathbf{k}\\ & \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ & P& Q& R\end{array}$$

---

6.计算补充

零向量方向是不确定的，可以指任意方向。
点乘：$\vec{a}\cdot \vec{a}=|\vec{a}{|}^2$
叉乘：$\vec{a}\times \vec{a}=0$
坐标轴$x,y,z$轴对应的单位方向向量分别为$\vec{i},\vec{j},\vec{k}$,其任意两两叉乘均为另外一个单位向量，方向由右手定则确定，详细结果如下：

	$\vec{i}$	$\vec{j}$	$\vec{k}$
$\vec{i}$	$\vec{i}\times \vec{i}=\vec{0}$	$\vec{i}\times \vec{j}=\vec{k}$	$\vec{i}\times \vec{k}=-\vec{j}$
$\vec{j}$	$\vec{j}\times \vec{i}=-\vec{k}$	$\vec{j}\times \vec{j}=\vec{0}$	$\vec{j}\times \vec{k}=\vec{i}$
$\vec{k}$	$\vec{k}\times \vec{i}=\vec{j}$	$\vec{k}\times \vec{j}=-\vec{i}$	$\vec{k}\times \vec{k}=\vec{0}$

---

暂定这样，后续根据情况进行补充……