变异系数

变异系数（Coefficient of variation）

[ 编辑]

什么是变异系数

　　变异系数又称“标准差率”，是衡量资料中各观测值变异程度的另一个统计量。当进行两个或多个资料变异程度的比较时，如果度量单位与平均数相同，可以直接利用标准差来比较。如果单位和（或）平均数不同时，比较其变异程度就不能采用标准差，而需采用标准差与平均数的比值（相对值）来比较。

　　标准差与平均数的比值称为变异系数，记为C.V。变异系数可以消除单位和（或）平均数不同对两个或多个资料变异程度比较的影响。

[ 编辑]

变异系数的计算

　　变异系数的计算公式为：

　　

　　变异系数越小，变异(偏离)程度越小，风险也就越小；反之，变异系数越大，变异(偏离)程度越大，风险也就越大。

　　例：已知某良种猪场A种成年母猪平均体重为190kg，标准差为10.5kg，而B种成年母猪平均体重为196kg，标准差为8.5kg，试问两个品种的成年母猪，那一个体重变异程度大。

　　此例观测值虽然都是体重，单位相同，但它们的平均数不相同，只能用变异系数来比较其变异程度的大小。

　　由于，A种成年母猪体重的变异系数：

　　B种成年母猪体重的变异系数：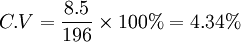 

　　所以，A种成年母猪体重的变异程度大于B种成年母猪。

　　注意，变异系数的大小，同时受平均数和标准差两个统计量的影响，因而在利用变异系数表示资料的变异程度时，最好将平均数和标准差也列出。