微积分的直观理解

在微积分中，我们进行定积分计算的时候一般是用牛顿莱布尼兹公式，不定积分计算也类似，都需要寻找原函数F(x)，但是如果想直观的理解微积分，我们需要顺着公式的反方向进行理解，下面我提供一种直观理解微积分的思路。

在以下的表达中，我们使用的定积分，但是为了方便可能会省略积分上下限，也可能不省略。

已知函数 y = f(x), 和积分区间[xa, xb]，区间两个端点xa, xb对应的函数值为ya, yb，yb - ya用积分的形式如何表示呢，我们将区间[xa, xb]分成无穷多段等长的小段，则每一小段的长度都趋于0，

（注意积分结果与分段方式无关，只需保证分段足够多的（无穷多段），每段长度足够小（趋于零）即可，不是等分也可以，只不过为了方便计算，我们将其等分），

x轴上每一小段的长度记做dx，y轴方向上，每一小段dxi都对应一个Δyi（i表示第i个小段），yb-ya 就等于把所有的Δy都加起来，即yb - ya = Δy1 + Δy2 + ▪▪▪ +Δyi + ▪▪▪ + Δyn，n表示最后一段，后续计算中我们可以让n趋于无穷大，注意Δy并不一定是正数。

我们在所有的段中任取一段Δyi，那么，其中o(dx)是dx的高阶无穷小，xi为第i段区间的左端点，我们记,则上式可写成

                                       

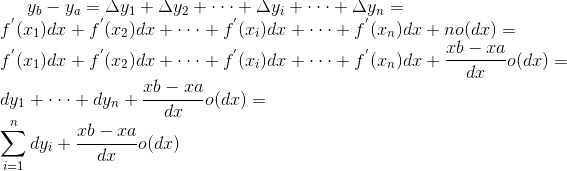
                                                                               等式1

其实上述中我们使用n*o(dx)来写入等式是欠妥当的，因为每一个积分小段里面的o(dx)不一定是相等的，这里写成n*o(dx)方便比较，即n是无穷大， o(dx)是无穷小，无穷大乘以无穷小，如何确定他们数量级的差别，和最终结果，n*o(dx)中的o(dx)可以理解为所有o(dx)的平均值。

等式两边求对n趋于无穷大求极限，由于左侧与n无关，所以左侧求极限形式不变

                                                   

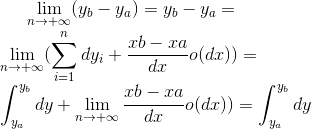
                                                                                 等式2

其中xb-xa为常数， o(dx)/dx在n趋于无穷大时，分子上是更高阶的无穷小，所以o(dx)/dx极限为0，乘以常数还是0，那么我们说一下为什么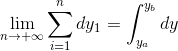，其实等式左边是定积分的定义，这样就没什么可说的了，但是这里还有一点和我们平时常见的积分方式不同，就是dy不是等分的，这和上述提到的“积分和如何分段无关，只要保证分段足够多的，每一段足够小即可” 就关联上了，其实这也没什么大惊小怪的，定积分的定义中重来没有规定必须等分，等分只是为了我们方便计算，下面用一个具体的函数来看一下:

                                        

y = x^2,  假设将x的积分区间等分成6段，可以看出对应y的微分dy不是均匀划分的， 如果将x的积分区间等分成n段，且n为无穷大，则dy虽然不是等分，但也满足分段足够多，每一小段足够小，所以无穷多个dy相加，结果就等于 在y上对常数函数1进行积分，即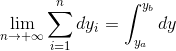，这时候就和上述函数图像没什么关系了，上述图像只是说明以y为自变量对常数函数1进行积分时，dy是如何分段的。 另外有的时候分段方式更为诡异，如果上图中的函数不是单调递增的，积分区间中既有递增区间又有递减区间，那么其中必有小段dy落在[ya, yb]之外，且这些落在[ya, yb]之外的dy必定有正有负，且它们的和为0，那在[ya, yb]之内的dy也满足每一段足够小，且分段足够多，它们相加仍然相当于在y上对常数函数1积分，即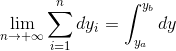

所以最终形式为

                                                                         

                                                                                  等式3

到这里感觉得到了一句废话，对常数1 在ya到yb上对y积分，结果显然是yb-ya，这是微积分初学者都知道的，但是其中的道理却不是所有人都能讲清楚的，下面我们将其替换成关于x的表达式（其实在等式1第三行，我们可以直接对等式两边求极限，即可得到关于x的表达式，更加明了，但没有使用y表示简洁）

                                                                        

                                                                                    等式4

至此，我们发现等式4 和牛顿莱布尼兹公式基本一致，只不过等式左右两边互换了一下，现在我们应该理解，为什么我说理解微积分的基本原理要和计算步骤反着来了吧， 证明中，我们活生生地将f(x)拆成了对其导函数进行积分的形式，但是计算过程中，我们却和证明过程完全反着用，因为我们更喜欢去繁就简，而不是反着来。

下面我们来说一说等式1第三行，如何直接得到关于x的表达式，我们已有的表达式如下：

两边对n求极限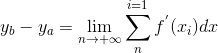，，和上述只有y的表达式一样，这里等式右侧是定积分的定义，且最初的假设中，我们是将dx作为等长分割的，这就比只有y的表达式更容易理解了，所以顺理成章就得到了等式4

 

以上是对定积分计算公式非严格的推导，如果看不懂，证明我写的很烂，就忘记它吧， 因为它不够直观，下面结合图形，介绍最直观的理解方式：

 

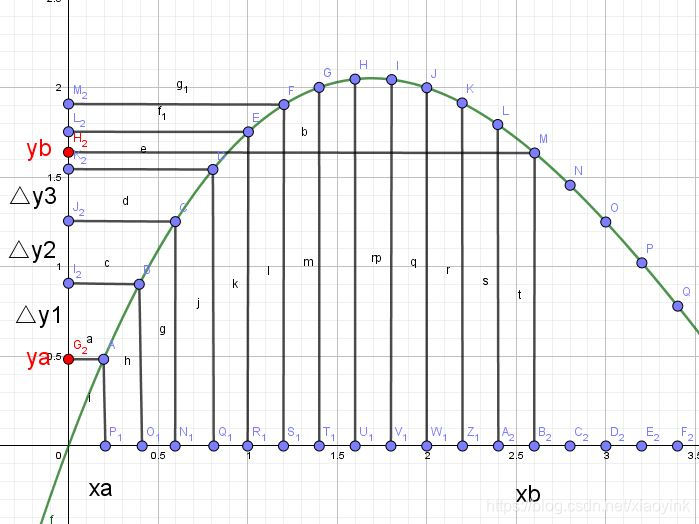
假设y=f(x)的图像如上图所示，那么取区间[xa, xb]的两端点的函数值 ya，yb， yb-ya如何表示呢？上面已经说过了：yb - ya = Δy1 + Δy2 + ▪▪▪ +Δyi + ▪▪▪ + Δyn， 在图中区间[xa, xb]上取任意第i个小段dx，放大后如下图，那么Δyi ≈ f‘(xi)*dxi

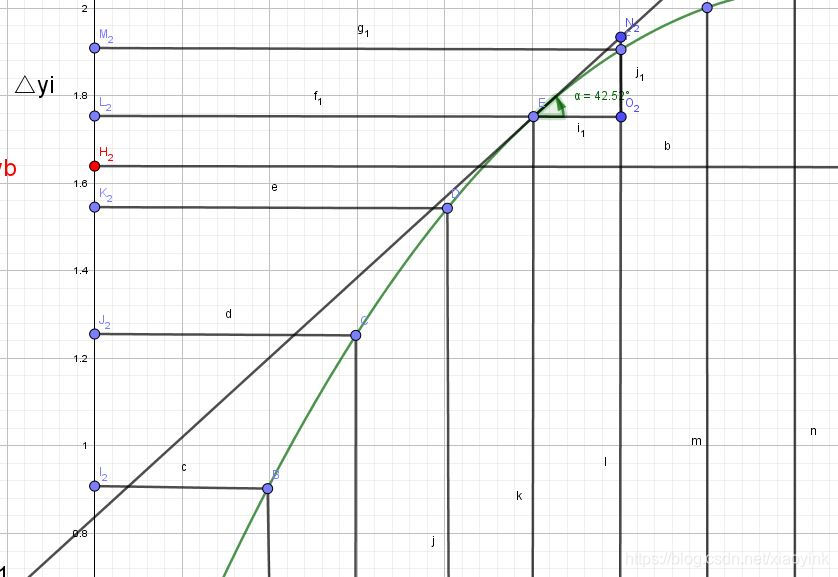
我们可以看到Δyi ≈ tanα * dx 其中tanα = f'(xi)，且当区间[xa, xb]分段分的越细，Δyi 和 tanα * dx越接近，那么

yb - ya = Δy1 + Δy2 + ▪▪▪ +Δyi + ▪▪▪ + Δyn ≈ f'(x1)dx + f'(x2)dx +  ▪▪▪ +f'(xi)dx +  ▪▪▪ + f'(xn)dx ，到这里我们直观的看到，区间[xa, xb]两个端点函数值的差yb-ya，就等于将区间[xa, xb]，分成无数段之后，每一段的长度dx 乘以每一小段 内任意点切线的斜率tanα，然后再依次累加，那 f'(x1)dx + f'(x2)dx +  ▪▪▪ +f'(xi)dx +  ▪▪▪ + f'(xn)dx （其中n为无穷大），就是定积分，所以理解微积分要结合原函数的图像进行理解，而非导函数的图像。

高中刚开始接触微积分的时候，总是盯着导函数的图像看，导函数图像和x坐标轴围成的面积 等于 定积分，为什么面积的计算等于自变量区间的两个端点所对应的原函数的函数值之差， 这困扰了我很久，一直盯着导函数的图像是很难理解的，但是如果盯着原函数的图像就很顺理成章了， 理解了这一点，接下来只需要去理解，对导函数的定积分恰好等于导函数图像和坐标轴围成的面积。这样就很容易理解微积分的计算了。