MATLAB 使用教程 ——

startup.m

软链接：希望将某个特定的文件夹链接到 MATLAB 启动时的路径。软链接（symbolic link）只是将一个路径指向另一个路径，确保 MATLAB 可以在启动时访问你指定的目录或文件夹，但是它并不会自动在 MATLAB 窗口中打开该文件夹。能在 MATLAB 命令行中使用 which startup 查找到 startup.m 的路径。

setx GATOOLS_ROOT "C:\Users\admin\Documents\east0\gatools" # windows 设置环境变量
echo %GATOOLS_ROOT%  # 查看是否设置成功

# cmd 窗口，需要以管理员身份运行，设置软链接
mklink "C:\Users\admin\Documents\MATLAB\startup.m" "%GATOOLS_ROOT%\startups\generic_startup.m"

• mklink 后不使用 /D 时，默认创建文件符号链接。/D 用于创建目录符号链接。
• C:\Users\Documents\MATLAB\startup.m是 MATLAB 默认路径下要创建的软链接路径。
• C:\path\to\your\folder 是你希望链接的实际文件夹路径。

如果你的目标是在 MATLAB 启动时直接打开某个文件夹，可以在 startup.m 中添加如下内容：

% 设置工作目录
cd('C:\Users\yourusername\Documents\MATLAB\gatools')

% 打开文件夹
open('C:\Users\yourusername\Documents\MATLAB\gatools')

绘图

在 MATLAB 中绘制函数图形的具体步骤如下：

1. 定义变量 x：通过设置 x 的范围和步长来定义变量。例如，x = linspace(-10, 10, 1000); 将在 -10 到 10 之间生成 1000 个等间隔的点。

2. 定义函数 y = f(x)：通过给定的 x 值计算 y，例如 y = sin(x);。

3. 调用 plot 命令：使用 plot(x, y) 绘制函数图形。

示例代码如下：

% Step 1: 定义变量 x
x = linspace(-10, 10, 1000);

% Step 2: 定义函数 y = f(x)
y = sin(x);

% Step 3: 调用 plot 命令绘制图形
plot(x, y);
title('Sine Function');
xlabel('x');
ylabel('sin(x)');
grid on; % 添加网格线

运行此代码后，会生成一个从 -10 到 10 的 sin(x) 函数的图形，并带有标题和轴标签。

二维线图

创建二维线图，使用 plot 函数。

例如，绘制在从 0 到 2π 的值组成的线性间距向量上的正弦函数：

x = linspace(0,2*pi);
y = sin(x);
plot(x,y)

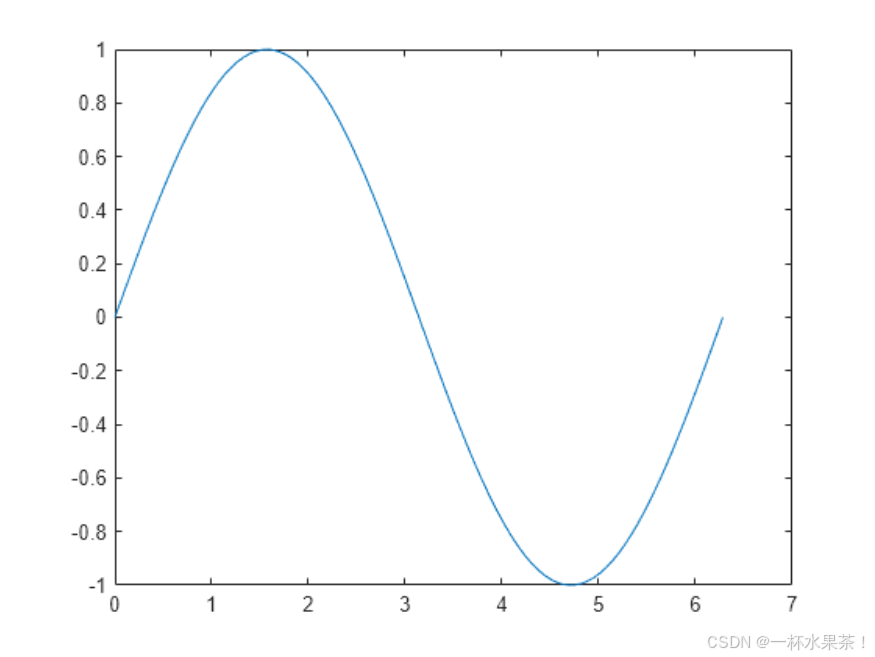
可以标记轴并添加标题。

xlabel("x")
ylabel("sin(x)")
title("Plot of the Sine Function")

通过向 plot 函数添加第三个输入参量，可以使用红色虚线绘制相同的变量。

plot(x,y,"r--")

r-- 为线条设定。每个设定可包含表示线条颜色、样式和标记的字符。标记是在绘制的每个数据点上显示的符号，例如，+、o 或 *。例如，g:* 请求绘制使用 * 标记的绿色点线。

MATLAB 包含了八个绘制图形的基本颜色选项，下表提供了显示的颜色以及相应的代码：

Color	Code
White	w
Black	k
Blue	b
Red	r
Cyan	c
Green	g
Magenta	m
Yellow	y

默认情况下，每次调用绘图函数、重置坐标区及其他元素以准备新绘图时，MATLAB 都会清空图窗。

使用 hold on 将绘图添加到现有图窗中，在使用 hold off 或关闭窗口之前，当前图窗窗口中会显示所有绘图。

x = linspace(0,2*pi);
y = sin(x);
plot(x,y)

hold on

y2 = cos(x);
plot(x,y2,":")
legend("sin","cos")

hold off

三维绘图

三维图通常显示一个由带两个变量的函数 $z=f(x,y)$ 定义的曲面图。

例如，对于给定的行向量和列向量 $x$ 和 $y$，每个向量包含 [-2,2] 范围内的 20 个点，计算 $z=x{e}^{-x^2-y^2}$。

x = linspace(-2,2,20);
y = x';
z = x .* exp(-x.^2 - y.^2);

然后，创建曲面图。

surf(x,y,z)

surf 函数及其伴随函数 mesh 以三维形式显示曲面图。

• surf 使用颜色显示曲面图的连接线和面。
• mesh 生成仅以颜色标记连接线条的线框曲面图。

多个绘图

tiledlayout 和 subplot 都可以在同一窗口的不同部分中显示多个绘图，但 tiledlayout 提供了更灵活的布局和标签控制。

例如，在图窗窗口中创建 2×2 布局。然后，每当您要某个绘图出现在下一区域中时，请调用 nexttile。

t = tiledlayout(2,2);
title(t,"Trigonometric Functions")
x = linspace(0,30);

nexttile
plot(x,sin(x))
title("Sine")

nexttile
plot(x,cos(x))
title("Cosine")

nexttile
plot(x,tan(x))
title("Tangent")

nexttile
plot(x,sec(x))
title("Secant")

常用函数

字符串

strmatch 函数：字符串匹配

strmatch 是一个用于匹配字符串的函数，它用于查找一个字符串是否与目标字符串完全或部分匹配。strmatch 是区分大小写的。

该函数会返回匹配字符串的位置或与目标字符串匹配的索引，通常用于字符串匹配的情况。

index = strmatch(str, strArray)

• str：要匹配的目标字符串，可以是一个字符串（字符向量）或字符串数组。
• strArray：字符串数组或一个字符串的单元格数组，包含多个字符串，strmatch 会检查每个字符串与目标字符串 str 的匹配情况。
• index：返回一个索引或匹配的位置。如果有多个匹配项，返回这些匹配项的位置。如果没有匹配项，则返回空数组。返回的 index 是 strArray 中与 str 匹配的字符串的索引。

用法一：查找匹配字符串的位置。

strArray = {'apple', 'banana', 'cherry', 'pineapple'};
index = strmatch('apple', strArray);
disp(index);  % 1 4

strmatch 找到了两个匹配的 “apple”，一个在数组的第 1 位，另一个在第 4 位。

用法二：检查字符串的某一部分字符。
检查字符串 date 的前四个字符是否是 “2024”。如果是，则将变量 year 设置为 2024。

date = '20241111';
if(strmatch(date(1:4),'2024'))
   year = 2024;
end  

存在性

exist 函数：检查是否存在

exist 是一个用于检查变量、函数、文件或其他对象是否存在的函数。它可以返回不同类型对象的存在性信息。

exist 的返回值有助于判断对象的类型和状态，通常与 if 语句结合使用，以确保代码在运行时能正确地处理缺失的文件或变量。

exist 函数的基本语法如下：

status = exist(name)
status = exist(name, 'type')

• name：要检查的对象的名称，通常是字符串或字符向量。它可以是变量、函数、文件、类、目录等的名称。
• ‘type’ (可选)：该参数指定要检查的对象类型。‘var’：变量，‘builtin’：内建函数，‘file’：文件，‘dir’：文件夹，‘class’：类。

返回的数字取决于 name 和 type 的组合：

• 0：对象不存在。
• 1：如果是变量，表示变量存在。

用法一：检查文件的存在性。
在处理文件时，通常会使用 exist 来检查文件是否存在。例如，在读取数据文件之前：

filename = 'data.txt';
if exist(filename, 'file') == 2
    data = load(filename);
else
    disp('File does not exist!');
end

用法二：检查变量的存在性。
在运行代码时，可以使用 exist 来确认变量是否已定义：

if exist('myVar', 'var') ~= 1  % 如果返回值不等于 1
    disp('Variable does not exist');
else
    disp('Variable exists');
end

用法三：检查变量是否存在，如果不存在或为空，赋默认值。

if(~exist('res') | isempty(res))
   res = 1.5;
end

isfield 函数：检查结构体中是否存在特定字段

isfield 是 MATLAB 中用于检测某个结构体中是否存在特定字段的函数。

其基本语法如下：

tf = isfield(S, 'fieldname')

• S：要检查的结构体。
• ‘fieldname’：需要检查是否存在的字段名称（字符串形式）。
• tf：返回一个布尔值，如果 fieldname 是结构体 S 中的字段，则返回 true；否则返回 false。

S.name = 'John';
S.age = 30;

% 检查是否存在 'name' 字段
isNameField = isfield(S, 'name')  % 返回 true

% 检查是否存在 'gender' 字段
isGenderField = isfield(S, 'gender')  % 返回 false

用法一：检查结构体中是否有某个字段，以便赋值。

if(isfield(objs,'data'))
   data  = objs.data;
else
   data = [];
end

文件相关

fileparts 函数：分解文件路径

下面的这行代码通过 mfilename('fullpath') 获取当前脚本的完整路径，并使用 fileparts 函数提取文件的路径部分（即 this_dir）。this_dir 存储了当前脚本所在的文件夹路径，即当前脚本的父目录。

[this_dir, ~, ~] = fileparts(mfilename('fullpath'));

fileparts 是 MATLAB 中用于分解文件路径的函数，它将一个完整的文件路径拆解成不同的部分，通常返回文件所在的目录路径、文件名和扩展名。语法如下：

[folder, name, ext] = fileparts(filepath)

• filepath：一个字符串或字符数组，表示完整的文件路径，包含文件所在的文件夹、文件名和扩展名。这个路径可以是绝对路径或相对路径。
• folder：返回文件路径的目录部分，即文件所在的文件夹的路径。如果 filepath 是文件名，则返回当前工作目录。
• name：返回文件的名称，不包括扩展名。
• ext：返回文件的扩展名（以点 . 开头），如果文件没有扩展名，则返回空字符串。

具体例子如，

filepath = 'C:\Users\admin\Documents\myfile.txt';
[folder, name, ext] = fileparts(filepath);

• folder = ‘C:\Users\admin\Documents’
• name = ‘myfile’
• ext = ‘.txt’

fullfile 函数：构建完整文件路径

与 fileparts 相对的是 fullfile 函数，用于将上面三部分构建成完整路径。

fileparts 可以用于从路径中提取文件夹和文件名部分，然后通过 fullfile 函数重新构建路径。

[folder, name, ext] = fileparts('C:\Users\admin\Documents\myfile.txt');
newpath = fullfile(folder, [name, '_new', ext]);
% 这会生成 C:\Users\admin\Documents\myfile_new.txt

脚本和函数 .m 文件

除了在 MATLAB 命令提示符下输入命令，MATLAB 还支持创建和运行脚本文件和函数文件。

• 脚本文件：包含一系列 MATLAB 命令的简单文本文件，扩展名为 .m。脚本文件通过在命令行中输入文件名来运行，可以共享变量并与工作区交互。
• 函数文件：也是扩展名为 .m 的文本文件，但包含定义函数的代码。函数有自己的局部变量，并且通过输入和输出参数进行交互。函数文件的基本结构如下：

  function [output1, output2] = myFunction(input1, input2)
      % Function body with operations on input variables
      output1 = input1 + input2;
      output2 = input1 * input2;
  end
  

通过这种方式，MATLAB 允许用户将代码封装成可重用的模块，从而提高代码的组织和可维护性。

MATLAB 创建并运行脚本文件

创建脚本文件，需要使用文本编辑器。

• 用命令创建脚本文件，如果想把 .m 文件存储在一个特定的文件夹如 progs 下，那么一定要提供整个路径。如果只有 edit prog1.m 命令则会在默认情况下，MATLAB 目录中创建文件。

mkdir progs    % create directory progs under default directory
chdir progs    % changing the current directory to progs
edit  prog1.m  % creating an m file named prog1.m

• 如果使用的是 IDE，选择 NEW -> Script。这也打开编辑器，并创建一个文件名为命名。输入代码后可以命名并保存文件。

在编辑器中输入以下代码，

NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
    + NonTeachingStaff;
disp(Total);

创建和保存文件后，运行脚本文件：

• 编辑器窗口中单击“Run”按钮或

• 只要在命令提示符下键入文件名（不含扩展名）：>> prog1

命令窗口提示显示的结果是：

6170

命令窗口输入命令，工作区显示变量

MATLAB 桌面包含的面板如下：

• 当前文件夹 - 此面板允许访问项目文件夹和文件。
• 命令窗口 - 这是主要区域，用户在命令行中输入命令，命令提示符(>>).
• 工作区 - 工作区显示所有变量，无论是创建的或从文件导入的变量。
• 命令历史记录 - 此面板显示或重新运行，在命令行中输入的命令。

命令在命令窗口输入

MATLAB 提供管理会话的各种命令：

命令	描述
clc	清除命令窗口。
clear	从内存中删除变量。
exist	检查存在的文件或变量。
global	声明变量为全局。
help	搜索帮助主题。
lookfor	搜索帮助关键字条目。
quit	停止 MATLAB。
who	列出当前变量。
whos	列出当前变量（长显示）。

使用 MATLAB 的时候有一些系统命令可以方便我们的操作，如在当前的工作区中可以使用系统命令保存为一个文件、加载文件、显示日期、列出目录中的文件和显示当前目录等。

MATLAB 常用的系统相关的命令：

命令	描述
cd	改变当前目录。
date	显示当前日期。
delete	删除一个文件。
diary	日记文件记录开/关切换。
dir	列出当前目录中的所有文件。
load	负载工作区从一个文件中的变量。
path	显示搜索路径。
pwd	显示当前目录。
save	保存在一个文件中的工作区变量。
type	显示一个文件的内容。
what	列出当前目录中的所有 MATLAB 文件。
wklread	读取 .wk1 电子表格文件。

MATLAB 用于工作数组、矩阵和向量的各种命令：

命令/函数	描述
cat	连接数组
find	查找非零元素的索引
length	计算元素数量
linspace	创建间隔向量
logspace	创建对数间隔向量
max	返回最大元素
min	返回最小元素
prod	计算数组元素的连乘积
reshape	重新调整矩阵的行数、列数、维数
size	计算数组大小
sort	排序每个列
sum	每列相加
eye	创建一个单位矩阵
ones	生成全 1 矩阵
zeros	生成零矩阵
cross	计算矩阵交叉乘积
dot	计算矩阵点积
det	计算数组的行列式
inv	计算矩阵的逆
pinv	计算矩阵的伪逆
rank	计算矩阵的秩
rref	将矩阵化成行最简形
cell	创建单元数组
celldisp	显示单元数组
cellplot	显示单元数组的图形表示
num2cell	将数值阵列转化为异质阵列
deal	匹配输入和输出列表
iscell	判断是否为元胞类型

MATLAB 提供了大量的绘制图表命令：

命令/函数	描述
axis	人工选择坐标轴尺寸
fplot	智能绘图功能
grid	显示网格线
plot	生成 XY 图
print	打印或绘图到文件
title	把文字置于顶部
xlabel	将文本标签添加到 x 轴
ylabel	将文本标签添加到 y 轴
axes	创建轴对象
close	关闭当前的绘图
close all	关闭所有绘图
figure	打开一个新的图形窗口
gtext	通过鼠标在指定位置放注文
hold	保持当前图形
legend	鼠标放置图例
refresh	重新绘制当前图形窗口
set	指定对象的属性，如轴
subplot	在子窗口中创建图
text	在图上做标记
bar	创建条形图
loglog	创建双对数图
polar	创建极坐标图像
semilogx	创建半对数图（对数横坐标）
semilogy	创建半对数图（对数纵坐标）
stairs	创建阶梯图
stem	创建针状图

变量在工作区显示

MATLAB 支持以下特殊变量和常量：

名称	描述
ans	默认的变量名，最近一次操作运算结果
eps	浮点数的相对误差
i, j	虚数单位，定义为 i² = j² = -1
Inf	代表无穷大
NaN	代表不定值（不是数字）
pi	圆周率

工作区包含在 MATLAB 中创建或从数据文件或其他程序导入的变量。例如，下列语句在工作区中创建变量 A 和 B。

A = magic(4);
B = rand(3,5,2);

whos   % 使用 whos 可以查看工作区的内容

桌面上的“工作区”窗格也会显示变量。

退出 MATLAB 后，工作区变量不会保留。使用 save 命令保存数据以供将来使用，

save myfile.mat

通过保存，系统会使用 .mat 扩展名将工作区保存在当前工作文件夹中一个名为 MAT 文件的压缩文件中。

要清除工作区中的所有变量，使用 clear 命令。

使用 load 将 MAT 文件中的数据还原到工作区。

load myfile.mat

矩阵和数组

矩阵和数组

MATLAB 是“matrix laboratory”的缩写形式。MATLAB 主要用于处理 整个的矩阵和数组，而其他编程语言大多逐个处理数值。

• 所有 MATLAB 变量都是多维数组，与数据类型无关。
• 矩阵是指通常用来进行线性代数运算的二维数组。

MATLAB 专门用于处理矩阵和数组操作。与其他编程语言相比，它能够更高效地处理这些数据结构，适用于线性代数、数据分析、图像处理等。

MATLAB 中矩阵和数组长什么样？

a = [1 2 3 4]   % 单行的叫数组，数组 a 包含四个元素，使用逗号 (,) 或空格分隔各元素

a = [1 3 5; 2 4 6; 7 8 10]     % 多行的叫矩阵，使用分号分隔各行

再直观地来看，

这是数组 a：

这是矩阵 a：

MATLAB 怎么用矩阵计算？

MATLAB 常用的运算符和特殊字符如下表所示：

符号	描述
+	加；加法运算符
-	减；减法运算符
*	标量和矩阵乘法运算符
.*	数组乘法运算符
^	标量和矩阵求幂运算符
.^	数组求幂运算符
\	矩阵左除
/	矩阵右除
.\	阵列左除
./	阵列右除
:	向量生成；子阵提取
( )	下标运算；参数定义
[ ]	矩阵生成
.	点乘运算，常与其他运算符联合使用
…	续行标志；行连续运算符
,	分行符（该行结果不显示）
;	语句结束；分行符（该行结果显示）
%	注释标志
'	引用符号和转置运算符
.'	非共轭转置运算符
=	赋值运算符

为了说明 MATLAB 如何使用矩阵进行计算，这里提供一些具体例子：

创建和操作矩阵

% 创建一个 3x3 的矩阵
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

% 创建一个列向量
B = [10; 20; 30];

% 矩阵乘法
C = A * B;

在这个例子中，A 是一个 3x3 的矩阵，B 是一个 3x1 的列向量。MATLAB 直接支持矩阵乘法 A * B，这在其他编程语言中可能需要手动编写嵌套循环实现。

创建矩阵的另一种方法是使用 ones、zeros 或 rand 等函数。例如，创建一个由零组成的 5×1 列向量。

z = zeros(5,1)

矩阵运算示例

% 创建矩阵
M = [1, 2; 3, 4];

% 计算矩阵的转置
M_T = M';

% 计算矩阵的逆
M_inv = inv(M);

% 矩阵元素逐个平方
M_squared = M .^ 2;

% 矩阵加法
N = [5, 6; 7, 8];
M_sum = M + N;

• M_T 是 M 的转置矩阵。
• M_inv 是 M 的逆矩阵，前提是 M 是可逆的。
• M_squared 逐个对 M 中的每个元素平方，而不是矩阵乘法。
• M_sum 是矩阵 M 和 N 的逐元素相加。

MATLAB 允许使用单一的算术运算符或函数来处理矩阵中的所有值。例如，a + 10 是对矩阵 a 的所有值都 +10， sin(a) 是对矩阵 a 的所有值取 sin 值。

使用 * 运算符执行标准矩阵乘法，这将计算行与列之间的内积。例如，确认矩阵乘以其逆矩阵可返回单位矩阵： p = a*inv(a)。
请注意，p 不是整数值矩阵。MATLAB 将数字存储为浮点值，算术运算可以区分实际值与其浮点表示之间的细微差别。

使用 format 命令可以显示多/少小数位数： format long ，format short。注意 format 仅影响数字显示，而不影响 MATLAB 对数字的计算或保存方式。

要执行元素级乘法（而非矩阵乘法），请使用 .* 运算符： p = a.*a

乘法、除法和幂的矩阵运算符分别具有执行元素级运算的对应数组运算符。例如，计算 a 的各个元素的三次方： a.^3

定义一个 3×3 的矩阵 a，

这是 a + 10 ，

这是 矩阵与其逆相乘得到单位矩阵， p = a*inv(a)，

使用 format long 显示更多小数位，

用 p = a.*a 执行元素级乘法（而非矩阵乘法），

使用 a.^3 计算元素级的矩阵的幂，

例如，在图像处理领域，图像可以表示为二维矩阵，其中每个元素代表 像素值。MATLAB 使得处理和分析这些矩阵变得简单。以下是一个灰度图像的示例操作：

% 读取图像并将其转换为灰度矩阵
I = imread('example.jpg');
grayImage = rgb2gray(I);

% 对灰度图像应用卷积操作
kernel = [1, 1, 1; 0, 0, 0; -1, -1, -1];
filteredImage = conv2(double(grayImage), kernel, 'same');

MATLAB 的核心特性就是它内置的矩阵和数组处理功能，这允许用户以自然的数学语法编写程序，而无需手动实现低级矩阵运算。这对于需要处理大量数据的工程和科学计算非常有用。

串联

串联是将数组或矩阵连接起来形成更大数组的过程。在 MATLAB 中，方括号 [] 是串联运算符，它用于水平或垂直拼接数组。

当两个数组在行方向上进行拼接时，称为水平串联。例如：

A = [1, 2, 3];
B = [4, 5, 6];

% 水平串联
C = [A, B];  % 结果是 C = [1, 2, 3, 4, 5, 6]

在这个示例中，A 和 B 是两个行向量，通过 [] 拼接后形成了新的行向量 C。

当两个数组在列方向上进行拼接时，称为垂直串联。例如：

D = [7; 8; 9];
E = [10; 11; 12];

% 垂直串联
F = [D; E];  % 结果是 F = [7; 8; 9; 10; 11; 12]'

在此例中，D 和 E 是列向量，通过 [] 垂直串联后形成了新的列向量 F。

可以将矩阵水平或垂直串联，但需要满足维度匹配的条件。例如：

M1 = [1, 2; 3, 4];
M2 = [5, 6; 7, 8];

% 水平串联矩阵
H = [M1, M2];
% 结果是 H = [1, 2, 5, 6;
%             3, 4, 7, 8]

% 垂直串联矩阵
V = [M1; M2];
% 结果是 V = [1, 2;
%             3, 4;
%             5, 6;
%             7, 8]

在水平串联 H 的情况下，矩阵的行数必须一致；而在垂直串联 V 中，矩阵的列数必须一致。

访问矩阵的元素

在 MATLAB 中，数组的索引从 1 开始。这与某些编程语言（如 Python、C 等）不同，这些语言的数组索引从 0 开始。

% 创建一个 3x3 的矩阵
M = [1, 2, 3; 4, 5, 6; 7, 8, 9];

% 访问矩阵的元素
element = M(2, 3);  % 结果是 6，表示第二行第三列的元素

% 访问第一行的所有元素
firstRow = M(1, :);  % 结果是 [1, 2, 3]

% 访问第三列的所有元素
thirdColumn = M(:, 3);  % 结果是 [3; 6; 9]

重要注意事项：

• MATLAB 的索引从 1 开始，这意味着第一个元素的索引是 1。
• 可以使用冒号运算符 : 来访问数组的范围，例如 A(2:4) 会访问 A 中从索引 2 到 4 的元素。
• 冒号还可以用于指定所有元素。例如，M(:, 2) 代表矩阵 M 的第二列的所有元素。

这种从 1 开始的索引对于 MATLAB 用户来说是标准，特别是在数学和工程应用中，因为它与线性代数中矩阵的常见表示方法一致。