多元线性回归（OLS+稳健误）python代码实现

撩本子高手

已于 2023-02-24 11:04:34 修改

阅读量9k

点赞数 3

分类专栏：数学建模文章标签： python 线性回归

于 2023-02-13 15:32:13 首次发布

本文链接：https://blog.csdn.net/xiaziqiqi/article/details/128989007

版权

数学建模专栏收录该内容

12 篇文章

订阅专栏

简介

多元线性回归主要适用于应变量和自变量具有较强的线性关系，且主要研究因变量（被解释变量）和自变量（解释变量）之间的相关关系，从而达到解释或者预测的作用。而且一般用于处理横截面数据，横截面数据一般为同一时间段的不同对象的数据，比如同一年中的各省份的GDP。

适用条件

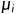自变量（X）和因变量（Y）具有线性关系（广义线性关系，只要能通过线性变化获得线性关系即可），具体呈现形式如下。 $\text{[math]}$ 是回归系数，又称为偏回归系数，而且截断项系数有较少意义。而且 $\text{[math]}$ 是扰动项，这里的扰动项默认是球形扰动项（具有同方差和无自相关性质，下面会有检验异方差的代码）

Y的类型为连续性数值变量（产量，收入等）

如果遇见定序变量（比如地区，文字）等，我们需要设置为虚拟变量，虚拟变量见下文所示，代码里面包含了构建虚拟变量。而且一般个数为定序变量的种类（n）-1（因为需要设置一个对照组）。

步骤

确定数据类型，为定序数值还是定量数据，然后根据数据进行预处理（比如取对数，标准化处理）和进行描述性统计。

对于可能出现内生性问题，我们选取核心解释变量（即X中跟Y有明显线性关系的变量，画图或者显著性检验证明），而且误差项 $\text{[math]}$ 中未出现跟自变量相关但未能显示，表达出来的系数。

对回归系数进行相关分析并且进行稳健性检验,这里运用的方法为最小二乘法（ols），即为机器学习中的最小化损失残差，而且进行参数更新等。

对变量进行VIF（方差膨胀因子）检验，一般情况，如果VIF>10，会出现比较严重的多重共线性。

实现代码

'''
VIF检验
参考：https://blog.csdn.net/mfsdmlove/article/details/124592619
OLS+稳健误回归多元回归模型
参考：https://cloud.tencent.com/developer/article/1675429
残差平方图
https://blog.csdn.net/qq_44763548/article/details/107472275
'''
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import wooldridge as woo
from statsmodels.formula.api import ols
from statsmodels.stats.diagnostic import het_white
import statsmodels.api


def calculate_nominal_vars(nominal_vars, data):
    for each in nominal_vars:
        print(each, ":")
        print(data[each].agg(['value_counts']).T)
        print("=" * 35)


def process_variables(nominal_vars_data, data):
    dummies = pd.get_dummies(nominal_vars_data)  # 自动命名虚拟变量，而且这里是选择某一个单一变量
    # 因为需要设置一个对照组，所以将每个nominal_vars生成的虚拟变量实际应用一般是变量数-1
    dummies.drop(columns=['C'], inplace=True)
    # dummies.sample()
    results = pd.concat(objs=[data, dummies], axis='colums')  # 按照列合并
    return results


def VIF_test(df, col_i):
    '''
    :param df: 整一份数据
    :param col_i: 被检测列名字,而且这里只能一列一列检测，所以这里需要注意一下，即为有关系
    :return:
    '''
    cols = list(df.colums)
    cols.remove(col_i)
    col_noti = cols
    formula = col_i + '~' + '+'.join(col_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1 - r2)


def white_test(res, X):
    '''
    :param:resid:残差
    :param:exog_het:用于white检验的自变量（只需要自变量的一阶形式，函数自动加入平方和交互作用项进行回归）
    :return:white_test_output,一共有'white_lm_statistic', 'white_lm_pval', 'white_F_statistic', 'white_F_pval'
    '''
    result_bp_test = het_white(res, X)
    white_test_output = pd.Series(result_bp_test[0:4],
                                  index=['white_lm_statistic', 'white_lm_pval', 'white_F_statistic', 'white_F_pval'])
    return white_test_output




def ols_regression(variables, data):
    '''
        小写的ols自带了截距项，但是大写的OLS并未带有截距项
        而且格式为固定 （因变量 ~ 自变量1 + 自变量2 + ······ + 自变量n）
        variables为固定格式即为str类型，而且为'price ~ area + bedrooms + bathrooms'
    '''
    lm = ols(variables, data=data).fit()
    return lm.summary().tables[1]


def ols_regression_robust_error(variables, data):
    '''

    :param variables:
    :param data:
    :return: 返回的是一个带有各种检验的表格
    White标准误（异方差稳健的标准误）：
    HC0:White（1980）提出的异方差稳健的标准误
    HC1:Mackinon and White（1985）提出的异方差稳健的标准误
    HC2:MacKinnon and White（1985）提出的异方差稳健的标准误
    HC3:MacKinnon and White（1985）提出的异方差稳健的标准误
    HAC:Newey-West标准误（异方差自相关稳健的标准误）：

    '''
    # hprice1 = woo.dataWoo('hprice1')
    # 适用white标准误（异方差稳定的标准误）
    reg_HC0 = ols(formula=variables, data=data)
    results_HC0 = reg_HC0.fit(cov_type='HC0', use_t=True)
    # 适用newey_west标准误（异方差自相关稳健的标准误）
    reg_HAC = ols(formula=variables, data=data)
    results_HAC = reg_HAC.fit(cov_type='HAC', use_T=True, cov_kwds={'maxlags': 1})  # maxlags表示滞后
    return results_HC0.summary().tables[1]

def get_predict(model, data, cloumns):
    model = model.fit()
    new_x = data.loc[data.Sales.notnull(), cloumns].values
    new_x = statsmodels.api.add_constant(new_x)  # sm2 = statsmodels.api
    y_predict = model.predict(new_x)
    return y_predict

def get_resid(predict, data):
    return data - predict
if __name__ == '__main__':
    hprice1 = woo.dataWoo('hprice1')
    print(ols_regression_robust_error('price ~ lotsize + sqrft + bdrms', data=hprice1))
    print()

有可能出现的问题

出现内生性

内生性，外生性

内生性为回归模型中的扰动项包含了所有跟已有的自变量具有一定相关性，但不是是自变量的元素。

为了检测出多重共线性问题，进行VIF（方差膨胀因子检验），VIF检验简单来说就是判断自变量之间是否具有相关性。我们采取了运用OLS+稳健误（怀特检验误）的方法，减少了异方差的影响。而且VIF如果大于10，即为证明出现严重的多重共线性。

外生性为误差项跟素所有的自变量均不相关。

数据为定序数据

数据出现定序数据（比如地域，年龄等），我们为了充分利用这一部分的数据，我们一般会采用构建虚拟变量等进行进行分析。而且构建的虚拟变量个数一般为n-1个。（n为某一变量出现的种类），虚拟变量的定义如下所示。

虚拟变量

虚拟变量的存在是为了充分利用这些自变量中有定性变量，例如性别、地域等变量。而且一般设置为0-1变量，命名一般为y_0,y_1,y_2等以此类推。具体如图所示，将地域信息转化为虚拟0-1变量。而且设置虚拟变量的时候，我们在回归之后一般会通过F统计量检验回归系数 $\text{[math]}$ 是否为联和显著。

3. 拟合优度 $\text{[math]}$ 较低

回顾拟合优度 $\text{[math]}$ ，在之前的拟合中有提及，具体公式如图所示，

注：SST为真实值和均值的差的平方和，SSE为真实值和拟合值的差的平均值，SSR为拟合值和均值的茶的平均值。

结论：如果是解释性模型，一般只要回归系数联合显著，则可以较少考虑拟合优度，如果是预测性模型，则需要以下的举措去调整拟合优度。

对模型进行调整，例如对给出数据取对数或者平方后再进行回归。取对数的好处为使得原来的不呈现正态分布的数据比较靠近正态分布，或者具有一定的经济学意义。

数据中可能有存在异常值或者数据的分布极度不均匀，剔除数据或者采取对抗学习生成较为平整的数据。

4. 出现多重共线性

虚拟变量的设置出现问题

当虚拟变量的个数是n（n为某一定序变量出现的种类，比如A,B地域，所以n=2），所以我们设置虚拟变量的时候应该设置虚拟变量的个数为n-1。（剩余的1是要作为对照组存在）

2. 扰动项出现异方差

我们一般用OLS+稳健误的方法解决干扰项出现异方差问题，使用该方案的原因如下：

（1）OLS估计出来的回归系数是无偏、一致的。

（2）假设检验无法使用（构造的统计量失效了）。

（3）OLS估计量不再是最优线性无偏估计量（BLUE）（不为最好）

无偏性和一致性

无偏性为用统计学的方法，去使得预估值和误差值一致。

一致性是在样本数量较多的时候，均值会在期望值收敛，即为 $\text{[math]}$ 。

同方差，异方差

同方差，指总体回归函数（求出回归系数之后的函数）中的随机误差项（干扰项）在解释变量（一定条件或者是解释变量不变的前提）条件下具有不变的方差。一组随机变量具备同方差即指线性回归的最小二乘法（OLS, Ordinary Least Squares）的残值服从均值为0，方差为 $\text{[math]}$ 的正态分布，即其干扰项必须服从随机分布。异方差跟其相反的定义。

异方差检验

怀特检验简介（推导过程这里其实有点蒙，所以只提供了代码和介绍）

当模型包含k=3个自变量时，怀特检验的代码

def white_test(res, X):
    '''
    :param:resid:残差
    :param:exog_het:用于white检验的自变量（只需要自变量的一阶形式，函数自动加入平方和交互作用项进行回归）
    :return:white_test_output,一共有'white_lm_statistic', 'white_lm_pval', 'white_F_statistic', 'white_F_pval'
    '''
    result_het_white_test = het_white(res, X)
    white_test_output = pd.Series(result_het_white_test[0:4],
                                  index=['white_lm_statistic', 'white_lm_pval', 'white_F_statistic', 'white_F_pval'])
    return white_test_output