BP反向传播算法

前言：

本来想把自己报告的ppt写成博客，后来公式打起来太麻烦了，不想再敲第二遍了。写一篇深入浅出，图文并茂的博客好难。

---

可以看斯坦福cs231n的课程，因为我发现很多人的博客的图和公式直接是截的那边的图。
http://cs231n.stanford.edu/syllabus.html

---

youtube上没有英文字幕，但是youtube会提供自动生成英文字幕，我的英文水平比较渣，有英文字幕还是听不懂，后来发现在网页上可以用0.5倍的速度观看。这个时候还可以。就算不看视频，看看ppt也是极好的。

正文：

BP反向传播算法明白了之后其实是比较简单，现在想想一开始阻碍自己明白的就是向量化的那种表达形式。
组会要做报告，做了一天的ppt，敲了很多公式，想写一篇日志发现已经无力再把那么多公式敲一遍了。简要的记录一发
首先是基本思想，求导的链式法则对于$f(t)=f(u(t),v(t))$，对$f$求偏导数$\frac{\partial f}{\partial t}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial t}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial t}$，其次要记住的一点就是对谁求偏导数，那么就把这个数当做变量，其他的都是常量。所以，对于$f(t)=f(u(t_1),v(t_2))$来说，$\frac{\partial f}{\partial t_1}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial t_1}$
BP算法就是基于上述的原理来进行求偏导的。看下面的简单例子:

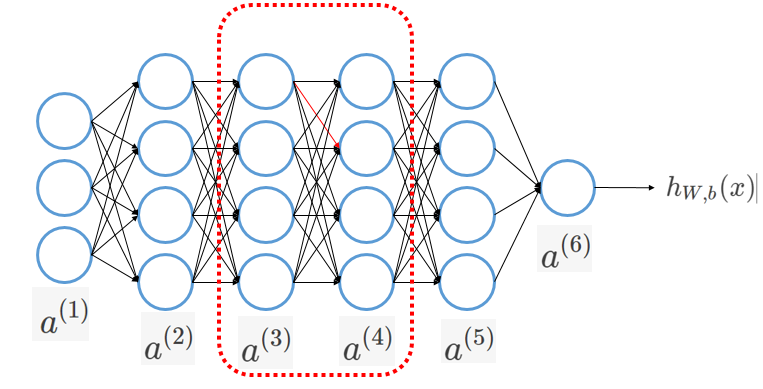
假如现在要求$\frac{\partial J}{\partial W^{(3)}_{21}}$也就是图中红色线的部分，$J$是损失函数。那么就要找到$J$中所有和$W^{(3)}_{21}$有关系的量。我们把图再拆解一下，如下图：

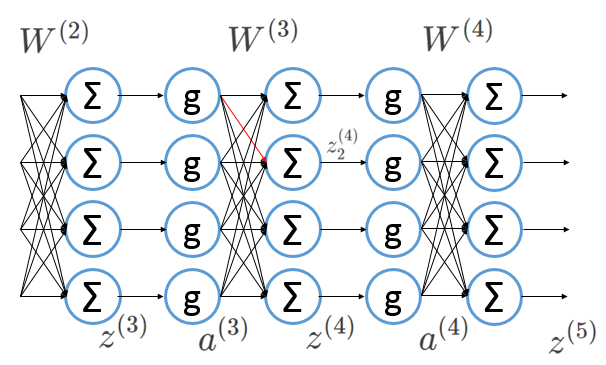
进一步拆解如下图：

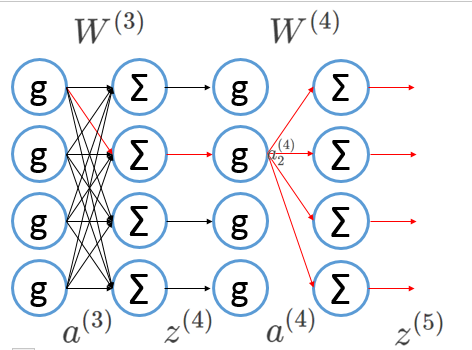
红色部分就是和$W^{(3)}_{21}$
可以看到第一个包含$W^{(3)}_{21}$的是$z^{(4)}_2$，所以，

$$\frac{\partial f}{\partial w^{(3)}_{21}}=a^{(3)}_1\frac{\partial J}{\partial z^{(4)}_2}$$ 接下来求后半部分 $\frac{\partial J}{\partial z^{(4)}_2}$，包含后半分的在图中也标出来了。所以，
$$\begin{align} \frac{\partial J}{\partial z^{(4)}_2}&=\frac{\partial J}{\partial a^{(4)}_2}\frac{\partial a^{(4)}_2}{\partial z^{(4)}_2} \\ &=\frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\sum_i\frac{\partial J}{\partial z^{(5)}_i}W^{(4)}_{i2} \\ \end{align}$$
这个时候考虑到 $\frac{\partial J}{\partial z^{(4)}_2}$和\frac{\partial J}{\partial z^{(5)}_2}的形式一样，所以，可以确定，在得知前一层的 $\frac{\partial J}{\partial z^{(l)}}$后可以求得后一层的偏导数。