堆排序&快速排序+优化 随机选取基准值+插入排序优化+相同元素聚集优化

写在前面

虽然很早就知道快排的思想了，但是并没有自己写过。其实写过最朴素的版本的，于是非常轻易的被卡成了$O(n^2)$的复杂度$233333$。最近心血来潮决定写一发优化的快排。

基准值优化

基准值的选取对时间复杂度的影响还蛮大的，固定选择某一个位置的值作为基准值的快排在处理有序、重复等数组时可能会达到$O(n^2)$的复杂度。关于这一项的优化呢，也有很多，常见的有三数取中、随机选取基准值等。对于前者其实就是在$a[l]、a[mid]、a[r]$中选择中间的那个值作为基准值，后者其实就是利用$rand()$函数在$a[l\dots \dots r]$中随机选择某个值作为基准值。作为欧皇，当然要用后者的办法！

插入排序优化

就是某位大佬研究发现，在$n$比较小，比如$5-20$时用插入排序替换快速排序会跑得更快，这个好像优化并不是很大，不过我还是加上了。

聚集优化

这个优化非常关键，否则你会发现即使你加上了其他优化，在处理重复元素很多的数组时还是可能会达到$O(n^2)$的复杂度。思路其实很简单，就是每次划分的时候把与基准值相等的元素全部放到一起。这样在处理重复元素很多的数组时可以快速缩减处理长度、减少递归次数。不过实现起来稍微复杂一点，能用的方法也有很多，我这里的思路是在划分的过程中先把与基准值相等的元素分别放到两端，最后再通过$swap()$函数把它们放到中间，具体看代码吧。这里给一张图方便大家理解：
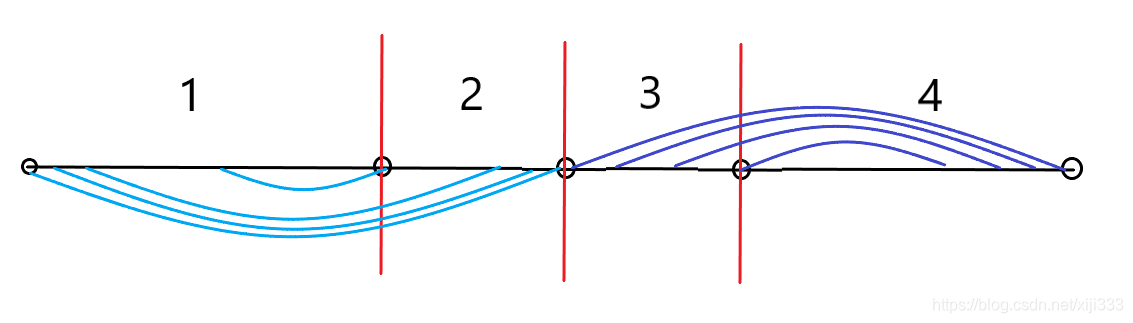通过划分把原序列划分成了四部分，部分$1$的值均等于基准值$base$，部分$2$的值均小于基准值$base$，部分$3$的值均大于基准值$base$，部分$4$的值均等于基准值$base$。这张图演示了如何进行聚集操作，对于$1、2$部分来说，如浅蓝色线所示，从两端向中间扩张并进行交换；对于$3、4$部分来说，同理。为什么要这样扩张？其他的方式行不行？这个问题我想留给大家思考，大家可以从$1、2$部分的长度入手，无非就三种情况嘛。

代码部分

https://www.luogu.com.cn/problem/P1177

给一道模板题，大家可以去练练手。有可能跑的比$sort$还快。不过还是觉的堆排序好写$orz$。

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;

const int maxn=1e5+5;
int a[maxn];

inline void insert_sort(int a[],int l,int r)
{
    int tmp,j;
    for(int i=l+1;i<=r;i++)
    {
        tmp=a[j=i];
        while(j!=l&&tmp<a[j-1])
            a[j]=a[j-1],--j;
        a[j]=tmp;
    }
}

inline pair<int,int> divide(int a[],int l,int r)
{
    int i,j;
    i=rand()%(r-l+1)+l;
    swap(a[i],a[l]);
    i=l+1,j=r;
    int posl=i,posr=j;
    while(i<j)
    {
        while(i<j&&a[i]<=a[l])
        {
            if(a[i]==a[l])
                swap(a[i],a[posl++]);
            ++i;
        }
        while(i<j&&a[j]>=a[l])
        {
            if(a[j]==a[l])
                swap(a[j],a[posr--]);
            --j;
        }
        if(i<j)
            swap(a[i],a[j]),i++,j--;
    }
    if(a[i]>a[l])
        --i;
    //[posl,i]均<a[l] [i+1,posr]均>a[l]
    //[l,posl-1]均=a[l] [posr+1,r]均=a[l]
    int idx1=l,idx2=r;
    for(int k=i;k>=posl&&idx1<posl;k--,idx1++)
        swap(a[k],a[idx1]);
    for(int k=i+1;k<=posr&&idx2>posr;k++,idx2--)
        swap(a[k],a[idx2]);
    int len1=i-posl+1,len2=posr-i;
    return pair<int,int>(l+len1-1,r-len2+1);
}

void quick_sort(int a[],int l,int r)
{
    if(r-l<=10)
        insert_sort(a,l,r);
    else
    {
        pair<int,int> p=divide(a,l,r);
        quick_sort(a,l,p.first);
        quick_sort(a,p.second,r);
    }
}

int main()
{
    srand(time(0));
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    quick_sort(a,0,n-1);
    for(int i=0;i<n;i++)
        printf("%d%c",a[i],i==n-1?'\n':' ');
    return 0;
}

来更新一波堆排序

这里以构建大根堆为例，且节点编号从$1$开始，那么对于任意一个节点$i$，如果存在子节点，那么左儿子的编号为$2\ast i$，右儿子的编号为$2\ast i+1$；其父节点的编号为$\lfloor i/2\rfloor$。大根堆其实就是满足这个性质的二叉堆：每一个节点的值都大于或等于其子节点的值。那么显然根节点的值就是所有值中最大的，由此不难想到堆排序的算法：$(1)$构建堆；$(2)$取出根节点的值放到另外一个数组中；$(3)$把根节点从堆中移除；$(4)$重复$(2),(3)$直到堆中没有元素。那么我们先来看看堆中常用的操作吧~

插入操作

不失一般性，我们假设在位置$pos$插入了一个值为$val$的元素，那么为了维持大根堆的性质，我们需要自底向上对堆进行修改。简单来说，就是判断$a[pos]$和$a[pos/2]$的值，如果前者大于后者，那么就交换这两个位置的值，然后递归的进行修改；否则函数就可以$return$了。

inline void Insert(int pos,int v)
{
    a[pos]=v;
    int idx;
    while(idx=(pos>>1))
    {
        if(a[idx]>=a[pos])
            break;
        swap(a[idx],a[pos]);
        pos=idx;
    }
    return ;
}

删除操作

很明显，删除操作是针对堆顶元素的。对于大根堆来说，通过删除操作可以得到所有元素的最大值。那么我们思考一下在删除堆顶之后，怎么维护堆的性质呢？不妨设堆有$n$个元素，我们可以交换$a[1],a[n]$，同时令$n=n-1$(因为堆顶被删除了嘛)。交换之后可能就不满足大根堆的性质了呀，所以我们要自顶向下对堆进行修改。简单来说，就是取$a[2\ast pos]$和$a[2\ast pos+1]$的最大值，设为$Max$，然后比较$a[pos]$和$Max$的值，如果后者大于前者，那么就要交换$a[pos]$和对应儿子的值，同时进入到对应的分支递归修改；否则函数就可以$return$了。
这里给出的是修改部分的代码：

inline void modify(int i,int n)
{
    int max_idx;
    while((i<<1)<=n)
    {
        max_idx=i<<1;
        if((max_idx|1)<=n&&a[max_idx|1]>a[max_idx])
            max_idx|=1;
        if(a[i]>=a[max_idx])
            break;
        swap(a[i],a[max_idx]);
        i=max_idx;
    }
    return ;
}

堆排序

有了这两个操作我们就可以得到堆排序的代码了！

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;

const int maxn=1e5+5;

int a[maxn];//大根堆
int b[maxn];//排序后的

inline void modify(int i,int n)
{
    int max_idx;
    while((i<<1)<=n)
    {
        max_idx=i<<1;
        if((max_idx|1)<=n&&a[max_idx|1]>a[max_idx])
            max_idx|=1;
        if(a[i]>=a[max_idx])
            break;
        swap(a[i],a[max_idx]);
        i=max_idx;
    }
    return ;
}

inline void Insert(int pos,int v)
{
    a[pos]=v;
    int idx;
    while(idx=(pos>>1))
    {
        if(a[idx]>=a[pos])
            break;
        swap(a[idx],a[pos]);
        pos=idx;
    }
    return ;
}

inline void heap_sort(int n)
{
    while(n>1)
    {
        b[n]=a[1];
        swap(a[1],a[n]);
        modify(1,--n);
    }
    b[1]=a[1];
    return ;
}

int main()
{
    int n,v;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&v);
        Insert(i,v);
    }
    heap_sort(n);
    for(int i=1;i<=n;i++)
        printf("%d ",b[i]);
    return 0;
}

建堆的复杂度

等一哈，还没完，如果你已经阅读了上面的代码，不难发现其建堆过程是暴力的把元素插到堆里面，不妨分析一下这么做的复杂度：为了方便计算，我们设它是一个满二叉树(一般来说形状是完全二叉树)，且一共有$k$层，那么节点总数$n=2^{k+1}-1$。假设当前插入的元素是在第$i$层，由于插入操作是自底向上的，所以最坏情况下它需要向上跳$i-1$次，那么我们可以得到：$$T=1\ast 0+2^1\ast 1+2^2\ast 2+\dots \dots +2^k\ast (k-1)$$

这不就是一个差比数列嘛，两边同乘$2$可得：
$$2\ast T=2^2\ast 1+2^3\ast 2+\dots \dots +2^{k+1}\ast (k-1)$$用该试减去第一个式子，化简可得：$$T=2^{k+1}\ast k-2$$由于$k$和$n$的关系，不难得到$T=O(nlgn)$，也就是说这种建堆方式的复杂度是$O(nlgn)$的。能不能优化呢？当然可以，还记得我们之前讲过的那个自顶向下的修改操作吗？我们完全可以先把$n$个元素放到堆中(随便放 不用维护堆的性质)，然后从第一个非叶子节点开始，调用修改操作。为什么不从$n$开始？因为只有有儿子的节点才需要修改。怎么得到第一个非叶子节点？根据完全二叉树的性质，$\lfloor n/2\rfloor$就是第一个非叶子节点的编号。代码如下所示：

inline void build(int n)
{
    for(int i=n>>1;i>=1;i--)//从非叶子节点开始
        modify(i,n);
    return ;
}

好，我们现在来分析一下这种方式的复杂度。方便起见，我们沿用上面的假设。由于修改操作是自顶向下的，所以对于第$i$层的节点，最坏情况下它需要向下跳$k-i$次，那么我们可以得到：$$T=1\ast (k-1)+2^1\ast (k-2)+\dots \dots +2^{k-1}\ast 1$$还是熟悉的差比数列，两边同乘$2$可得：$$2\ast T=2\ast (k-1)+2^2\ast (k-2)+\dots \dots +2^k\ast 1$$相减化简可得：$$T=2^{k+1}-1-k$$由$n$和$k$的关系不难得到：$T=O(n)$。所以我们可以采用这种更加快速的建堆方式。

最终版代码

又到了最愉快的模板题时间！
https://www.luogu.com.cn/problem/P1177

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;

const int maxn=1e5+5;

int a[maxn];//大根堆
int b[maxn];//排序后的

inline void modify(int i,int n)
{
    int max_idx;
    while((i<<1)<=n)
    {
        max_idx=i<<1;
        if((max_idx|1)<=n&&a[max_idx|1]>a[max_idx])
            max_idx|=1;
        if(a[i]>=a[max_idx])
            break;
        swap(a[i],a[max_idx]);
        i=max_idx;
    }
    return ;
}

inline void build(int n)
{
    for(int i=n>>1;i>=1;i--)//从非叶子节点开始
        modify(i,n);
    return ;
}

inline void heap_sort(int n)
{
    while(n>1)
    {
        b[n]=a[1];
        swap(a[1],a[n]);
        modify(1,--n);
    }
    b[1]=a[1];
    return ;
}

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    build(n);
    heap_sort(n);
    for(int i=1;i<=n;i++)
        printf("%d ",b[i]);
    return 0;
}