Tarjan算法与无向图连通性(割点\割边\双连通分量\缩点)

最新推荐文章于 2023-08-12 01:05:44 发布

csu_xiji

最新推荐文章于 2023-08-12 01:05:44 发布

阅读量731

点赞数 1

分类专栏： tarjan

本文链接：https://blog.csdn.net/xiji333/article/details/99630047

版权

tarjan 专栏收录该内容

17 篇文章 0 订阅

订阅专栏

$T a r j a n$ 算法与无向图连通性

无向图的割点与桥：

给定无向连通图 $G = (V, E)$ ：
若对于 $x\in V$ ，从图中删去节点 $x$ 以及所有与 $x$ 关联的边之后， $G$ 分裂成两个或两个以上不相连的子图，则称 $x$ 为 $G$ 的割点。
若对于 $e\in E$ ，从图中删去边 $e$ 之后， $G$ 分裂成两个不相连的子图，则称 $e$ 为 $G$ 的桥或割边。

时间戳：

在图的深度优先遍历过程中，按照每个节点第一次被访问的时间顺序，给予 $N$ 个节点 $1 - N$ 的整数标记。这些标记就叫做时间戳。(其实和 $d f s$ 序是一个东西)

搜索树：

在无向连通图中任选一个节点出发进行深度优先遍历，每个点只访问一次。所有发生递归的边 $(x, y)$ (换言之，从 $x$ 到 $y$ 是对 $y$ 的第一次访问)构成一棵树，我们把它称为"无向连通图的搜索树"。如下图所示：

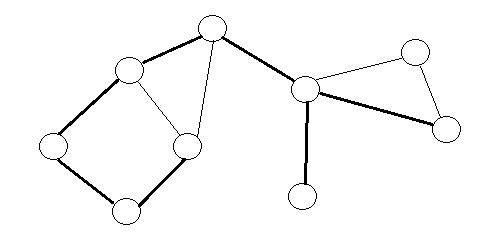
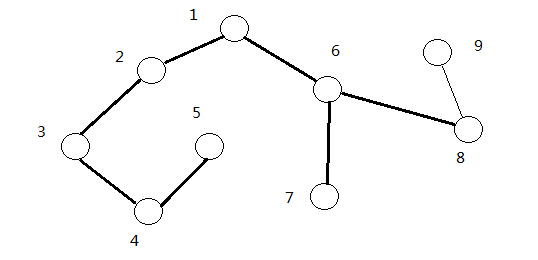
追溯值：

除了时间戳以外， $T a r j a n$ 算法还引入了一个"追溯值" $l o w [x]$ 。设 $s u b t r e e (x)$ 表示搜索树中以 $x$ 为根的子树。 $l o w [x]$ 定义为以下节点的时间戳的最小值：
1. $s u b t r e e (x)$ 中的节点。
2.通过 $1$ 条不在搜索树上的边，能够到达 $s u b t r e e (x)$ 的节点。
以上图为例，假设时间戳就是节点编号。 $subtree(2)=\{2,3,4,5\}$ ，另外节点 $1$ 通过不在搜索树上的边 $(1, 5)$ 能够到达 $s u b t r e e (2)$ 。所以 $l o w [2] = 1$ 。
根据定义，为了计算 $l o w [x]$ ，应该先令 $l o w [x] = d f n [x]$ ，然后考虑从 $x$ 出发的每条边 $(x, y)$ ：
若在搜索树上 $x$ 是 $y$ 的父节点，则令 $l o w [x] = m i n (l o w [x], l o w [y])$ 。
若无向边 $(x, y)$ 不是搜索树上的边，则令 $l o w [x] = m i n (l o w [x], d f n [y])$ 。

割边判定法则：

无向边 $(x, y)$ 是桥，当且仅当搜索树上存在 $x$ 的一个子节点 $y$ ，满足： $d f n [x] < l o w [y]$ 根据定义， $d f n [x] < l o w [y]$ 说明从 $s u b t r e e (y)$ 出发，在不经过 $(x, y)$ 的前提下，不管走哪条边都无达到 $x$ 或者比 $x$ 更早访问的节点。若把 $(x, y)$ 删除，则 $s u b t r e e (y)$ 就形成了一个封闭的环境，因此 $(x, y)$ 是割边。反之，若不存在这样的子节点 $y$ ，使得 $d f n [x] < l o w [y]$ ，则说明每个 $s u b t r e e (y)$ 都能绕行其他边到达 $x$ 或者比 $x$ 更早访问的节点， $(x, y)$ 自然就不是割边。
下面给出一个程序求出一张无向图中所有的桥，注意我们处理的是无向图，因此一条边要存储两次，用链式前向星存图的话同一条边存储的编号是： $2, 3 、 4, 5 、 6, 7$ 这样成对出现的，那么如果我们从 $0$ 号边进入了一个新的节点，就意味着 $0, 1$ 号边都是搜索树上的边，不能用 $d f n [y]$ 更新 $l o w [x]$ 。
求无向图中的所有桥：

#include<iostream>
#include<cstdio>
using namespace std;

const int maxn=1e5+5;

struct edge
{
    int to,nxt;
}Edge[maxn<<1];

bool bridge[maxn<<1];
int head[maxn],dfn[maxn],low[maxn];
int n,m,tot,num;

inline void addedge(int x,int y)
{
    Edge[++tot].to=y,Edge[tot].nxt=head[x],head[x]=tot;
}

void tarjan(int x,int in_edge)
{
    int y;
    dfn[x]=low[x]=++num;
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(!dfn[y])//未访问过的节点
        {
            tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if(low[y]>dfn[x]) //桥
                bridge[i]=bridge[i^1]=1;
        }
        else if(i!=(in_edge^1))//别忘了括号
            low[x]=min(low[x],dfn[y]);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int x,y;
    tot=1;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
    for(int i=2;i<tot;i+=2)
        if(bridge[i])
            printf("%d %d\n",Edge[i^1].to,Edge[i].to);
    return 0;
}

割点判定法则：

若 $x$ 不是搜索树的根节点(深度优先遍历的起点)，则 $x$ 是割点当且仅当搜索树上存在 $x$ 的一个子节点 $y$ ，满足： $d f n [x] < = l o w [y]$

特别地，若 $x$ 是搜索树的根节点，则 $x$ 是割点当且仅当搜索树上至少存在两个子节点 $y_{1},y_{2}$ 满足上述条件(为什么是两个点？想一下当图为一条线时的情况)。证明方法与上面割边的情况类似，不再赘述。上面的那个例子中的两个割点是 $1$ 和 $6$ 。且因为此处判别符号是 $< =$ ，因此不需要考虑父节点和重边的问题。
求无向图中所有的割点：

#include<iostream>
#include<cstdio>
using namespace std;

const int maxn=1e5+5;

struct edge
{
    int to,nxt;
}Edge[maxn<<1];

bool cut[maxn];
int head[maxn],dfn[maxn],low[maxn];
int n,m,tot,num,root;

inline void addedge(int x,int y)
{
    Edge[++tot].to=y,Edge[tot].nxt=head[x],head[x]=tot;
}

void tarjan(int x)
{
    int y,flag=0;
    dfn[x]=low[x]=++num;
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(!dfn[y])//未访问过的节点
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]) 
            {
                ++flag;
                if(x!=root||flag>=2)
                    cut[x]=1;
            }
        }
        else
            low[x]=min(low[x],dfn[y]);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int x,y;
    tot=1;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            root=i,tarjan(i);
    for(int i=1;i<=n;i++)
        if(cut[i])
            printf("%d ",i);
    return 0;
}

例题洛谷 P3388
例题 BZOJ 1123

无向图的双连通分量：

若一张无向连通图不存在割点，则称它为"点双连通图"。若一张无向连通图不存在桥，则称它为"边双连通图"。无向图的极大点双连通子图称为"点双连通分量"，简记为" $v - D C C$ "。无向图的极大边双连通子图称为"边双连通分量"，简记为" $e - D C C$ "，二者统称为"双连通分量"，简记为" $D C C$ "。
定理：
一张无相连通图是"点双连通图"，当且仅当满足下列两个条件之一：
1.图的顶点数不超过2。
2.图中任意两点都同时包含在至少一个简单环中。简单环指的是不自交的环。
一张无向连通图是"边双连通图"，当且仅当任意一条边都包含在至少一个简单环中。
证明略去。

边双连通分量( $e - D C C$ )的求法：

求出无向图中的所有桥，并把桥都删除后，图会分成若干个连通块，每一个连通块都是一个边双连通分量。如图：

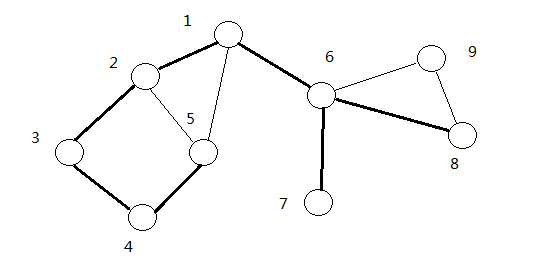
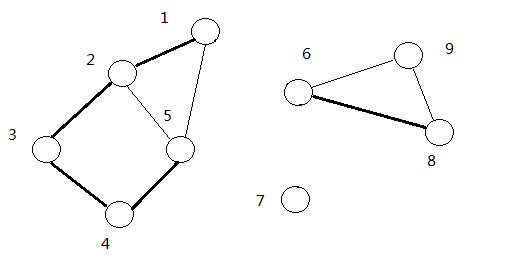
因此在 $t a r j a n$ 求割边的算法之后，进行 $d f s$ 求连通块即可(不经过桥边)。

#include<iostream>
#include<cstdio>
using namespace std;

const int maxn=1e5+5;

struct edge
{
    int to,nxt;
}Edge[maxn<<1];

bool bridge[maxn<<1];
int head[maxn],dfn[maxn],low[maxn];
int n,m,tot,num;

inline void addedge(int x,int y)
{
    Edge[++tot].to=y,Edge[tot].nxt=head[x],head[x]=tot;
}

void tarjan(int x,int in_edge)
{
    int y;
    dfn[x]=low[x]=++num;
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(!dfn[y])//未访问过的节点
        {
            tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if(low[y]>dfn[x]) //桥
                bridge[i]=bridge[i^1]=1;
        }
        else if(i!=(in_edge^1))//别忘了括号
            low[x]=min(low[x],dfn[y]);
    }
}

int id[maxn],dcc;//dcc个边双连通分量
void dfs(int x)
{
    int y;
    id[x]=dcc;
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(id[y]||bridge[i])
            continue;
        dfs(y);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int x,y;
    tot=1;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
    for(int i=1;i<=n;i++)
        if(!id[i])
            ++dcc,dfs(i);
    return 0;
}

$e - D C C$ 的缩点：

把每个 $e - D C C$ 看做一个节点，把桥边 $(x, y)$ 看作连接编号为 $i d [x]$ 和 $i d [y]$ 的 $e - D C C$ 对应节点的无向边，会产生一棵树(若原来无向图不连通则会产生森林)。这种把 $e - D C C$ 收缩为一个节点的方法就称为"缩点"。

#include<iostream>
#include<cstdio>
using namespace std;

const int maxn=1e5+5;

struct edge
{
    int to,nxt;
}Edge[maxn<<1];

int head_sd[maxn];
edge sd[maxn<<1];//e-DCC 缩点后的树
int cnt;
bool bridge[maxn<<1];
int head[maxn],dfn[maxn],low[maxn];
int n,m,tot,num;

inline void addedge(int x,int y)//存图
{
    Edge[++tot].to=y,Edge[tot].nxt=head[x],head[x]=tot;
}

inline void addedge_sd(int x,int y)//e-Dcc 缩点后的树
{
    sd[++cnt].to=y,sd[cnt].nxt=head_sd[x],head_sd[x]=cnt;
}

void tarjan(int x,int in_edge)
{
    int y;
    dfn[x]=low[x]=++num;
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(!dfn[y])//未访问过的节点
        {
            tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if(low[y]>dfn[x]) //桥
                bridge[i]=bridge[i^1]=1;
        }
        else if(i!=(in_edge^1))//别忘了括号
            low[x]=min(low[x],dfn[y]);
    }
}

int id[maxn],dcc;//dcc个边双连通分量
void dfs(int x)
{
    int y;
    id[x]=dcc;
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(id[y]||bridge[i])
            continue;
        dfs(y);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int x,y;
    tot=1;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
    for(int i=1;i<=n;i++)
        if(!id[i])
            ++dcc,dfs(i);
    cnt=1;
    for(int i=2;i<=tot;i++)
    {
        int x=Edge[i^1].to,y=Edge[i].to;
        if(id[x]==id[y])
            continue;
        addedge_sd(id[x],id[y]);
        addedge_sd(id[y],id[x]);
    }
    cout<<dcc<<endl;
    for(int i=2;i<cnt;i+=2)//可能会有重边
        cout<<sd[i^1].to<<' '<<sd[i].to<<endl;
    return 0;
}

点双连通分量( $v - D C C$ )的求法：

点双连通分量是一个很容易误解的概念。它与删除割点后图中剩余的连通块是不一样的。若某个节点为孤立点，则它自己单独构成一个 $v - D C C$ 。除了孤立点之外，点双连通分量的大小至少为 $2$ 。虽然桥不属于任何 $e - D C C$ ，但是割点可能属于多个 $v - D C C$ ，看图：(割点为 $1 、 6$ ，有 $4$ 个点连通分量粗线连接的点)

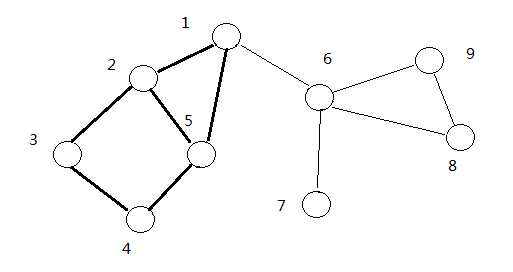
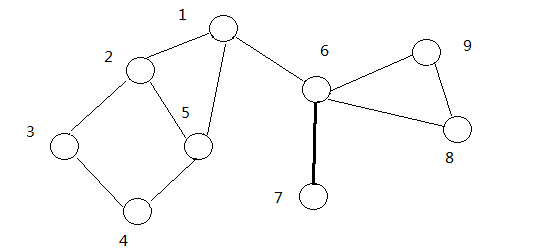
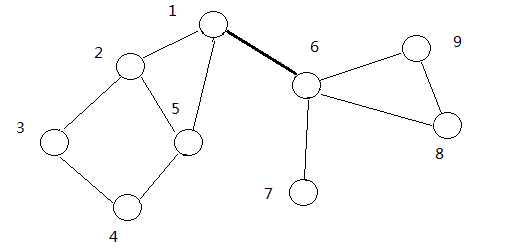
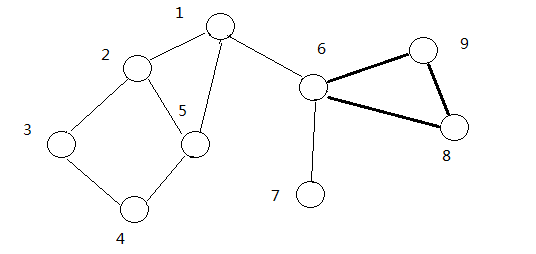
为了求出点双连通分量，需要在 $t a r j a n$ 算法中维护一个栈，并按照如下方法维护栈中的元素：
1.当一个节点第一次被访问时，该节点入栈。
2.当割点判定法则中的条件 $d f n [x] < = l o w [y]$ 成立时，无论 $x$ 是否为根，都要：
(1)从栈顶不断弹出节点，直至节点 $y$ 被弹出。
(2)刚才弹出的所有节点与节点 $x$ 一起构成一个 $v - D C C$ 。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;

const int maxn=1e5+5;

struct edge
{
    int to,nxt;
}Edge[maxn<<1];

vector<int> dcc[maxn];//点双连通分量
bool cut[maxn];
int head[maxn],dfn[maxn],low[maxn],Stack[maxn];
int n,m,tot,num,root,top,cnt;

inline void addedge(int x,int y)
{
    Edge[++tot].to=y,Edge[tot].nxt=head[x],head[x]=tot;
}

void tarjan(int x)
{
    int y,flag=0;
    dfn[x]=low[x]=++num;
    Stack[++top]=x;
    if(x==root&&head[x]==0)//孤立点
    {
        dcc[++cnt].push_back(x);
        return ;
    }
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(!dfn[y])//未访问过的节点
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]) 
            {
                ++flag;
                if(x!=root||flag>=2)
                    cut[x]=1;
                cnt++;
                int z;
                do
                {
                    z=Stack[top--];
                    dcc[cnt].push_back(z);
                }while(z!=y);
                dcc[cnt].push_back(x);
            }
        }
        else
            low[x]=min(low[x],dfn[y]);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    int x,y;
    tot=1;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            root=i,top=0,tarjan(i);
    for(int i=1;i<=cnt;i++)
    {
        cout<<"v-DCC #"<<i<<":";
        for(int j=0;j<dcc[i].size();j++)
            cout<<dcc[i][j]<<' ';
        cout<<endl;
    }
    return 0;
}

$v - D C C$ 的缩点：

$v - D C C$ 的缩点比 $e - D C C$ 要复杂一些，因为一个割点可能属于多个 $v - D C C$ 。设图中共有 $p$ 个割点和 $t$ 个 $v - D C C$ 。我们建立一张包含 $p + t$ 个节点的新图，把每个 $v - D C C$ 和每个割点都作为新图中的节点，并在每个割点与包含它的所有 $v - D C C$ 之间连边，组成的新图依然是一棵树(森林)。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;

const int maxn=1e5+5;

struct edge
{
    int to,nxt;
}Edge[maxn<<1];

int id[maxn];
int head_sd[maxn];
edge sd[maxn<<1];//缩点后的树
vector<int> dcc[maxn];//点双连通分量
bool cut[maxn];
int head[maxn],dfn[maxn],low[maxn],Stack[maxn];
int n,m,tot,num,root,top,cnt,tol;

inline void addedge(int x,int y)
{
    Edge[++tot].to=y,Edge[tot].nxt=head[x],head[x]=tot;
}

inline void addedge_sd(int x,int y)
{
    sd[++tol].to=y,sd[tol].nxt=head_sd[x],head_sd[x]=tol;
}

void tarjan(int x)
{
    int y,flag=0;
    dfn[x]=low[x]=++num;
    Stack[++top]=x;
    if(x==root&&head[x]==0)//孤立点
    {
        dcc[++cnt].push_back(x);
        return ;
    }
    for(int i=head[x];i;i=Edge[i].nxt)
    {
        y=Edge[i].to;
        if(!dfn[y])//未访问过的节点
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]) 
            {
                ++flag;
                if(x!=root||flag>=2)
                    cut[x]=1;
                cnt++;
                int z;
                do
                {
                    z=Stack[top--];
                    dcc[cnt].push_back(z);
                }while(z!=y);
                dcc[cnt].push_back(x);
            }
        }
        else
            low[x]=min(low[x],dfn[y]);
    }
}

int new_id[maxn];//割点的新编号 从cnt+1开始

int main()
{
    scanf("%d%d",&n,&m);
    int x,y;
    tot=1;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            root=i,top=0,tarjan(i);
    num=cnt;
    for(int i=1;i<=n;i++)
        if(cut[i])
            new_id[i]=++num;
    tol=1;
    for(int i=1;i<=cnt;i++)
    {
        for(int j=0;j<dcc[i].size();j++)
        {
            int x=dcc[i][j];
            if(cut[x])
            {
                addedge_sd(i,new_id[x]);
                addedge_sd(new_id[x],i);
            }
            else
                id[x]=i;//除割点外 其他点仅属于1个v-DCC
        }
    }
    for(int i=2;i<tol;i+=2)
        cout<<sd[i^1].to<<' '<<sd[i].to<<endl;
    return 0;
}

csu_xiji

关注

1
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
Tarjan算法与无向图连通性(割点\割边\双连通分量\缩点)

TarjanTarjanTarjan算法与无向图连通性无向图的割点与桥：给定无向连通图G=(V,E)G=(V,E)G=(V,E)：若对于x∈Vx\in Vx∈V，从图中删去节点xxx以及所有与xxx关联的边之后，GGG分裂成两个或两个以上不相连的子图，则称xxx为GGG的割点。若对于e∈Ee\in Ee∈E，从图中删去边eee之后，GGG分裂成两个不相连的子图，则称eee为GGG的桥或割边...
复制链接

扫一扫