高数_第3章重积分_在极坐标下计算二重积分

一  在极坐标定下限， 上限是怎么确定的？

注意：  极坐标下不需要交换积分次序

1. 在计算极坐标的重积分是， 都是写成 

∫dθ ∫f(x,y) rdr  形式，  就是说dθ 写在前面

2. 由二重积分的定义，可得出极坐标下的二重积分为

 也就是说，在极坐标下，被积函数中的x,  y分别用 x = rcosθ,  y= rsinθ 去代换， 将dσ用dσ=rdrdθ去代换。

3. 接下来看例题

例1：  计算二重积分 , 其中D为圆x²  + y² = 1及 x² + y² = 4与直线y=x,  y=0所围的第一象限的区域。 

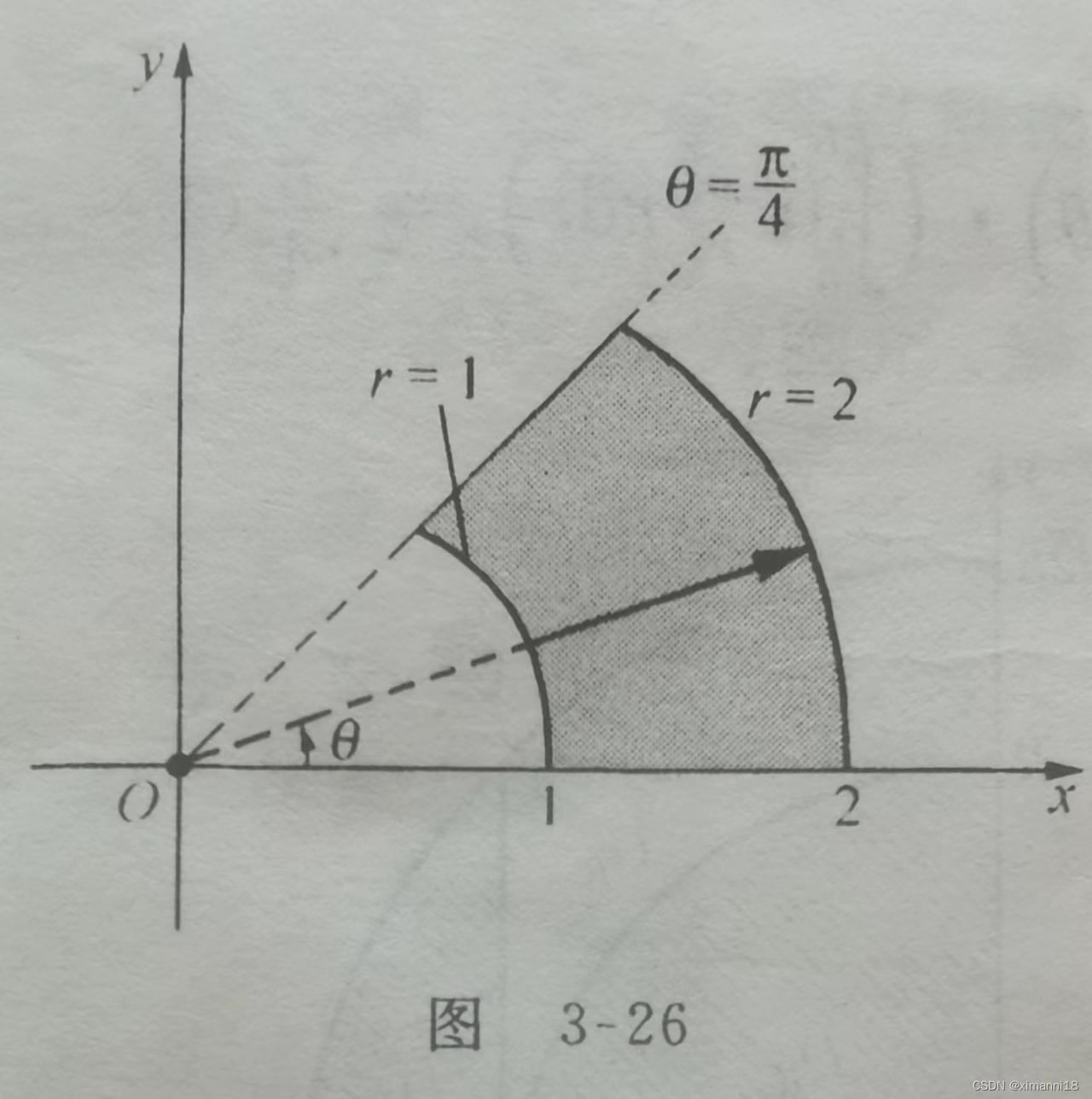
解：将极坐标变换 x = rcosθ, y=rsinθ 代入到边界方程中去， 边界 x²  + y²  = 1及 x²  + y² =4在极坐标下的方程分别为 r=1 和  r=2,

它们依次是近边界和远边界， 直线y=x 转变为rsinθ = rcosθ, 则 rsinθ/rcosθ = tanθ = 1, 所以θ = 

π/4;

直线y=0即为rsinθ = 0,  所以θ =0。

沿着与x轴的夹角为θ的射线， 从近边界r=1出发的箭头穿过积分区域指向远边界r=2,  且当

θ从0到 π/4时， 这此箭头扫过了整个积分区域，如图3-26. 于是在极坐标下，

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

接下来，我们看一个例题

解：积分区域D如图3-17所示

  

 

 

 

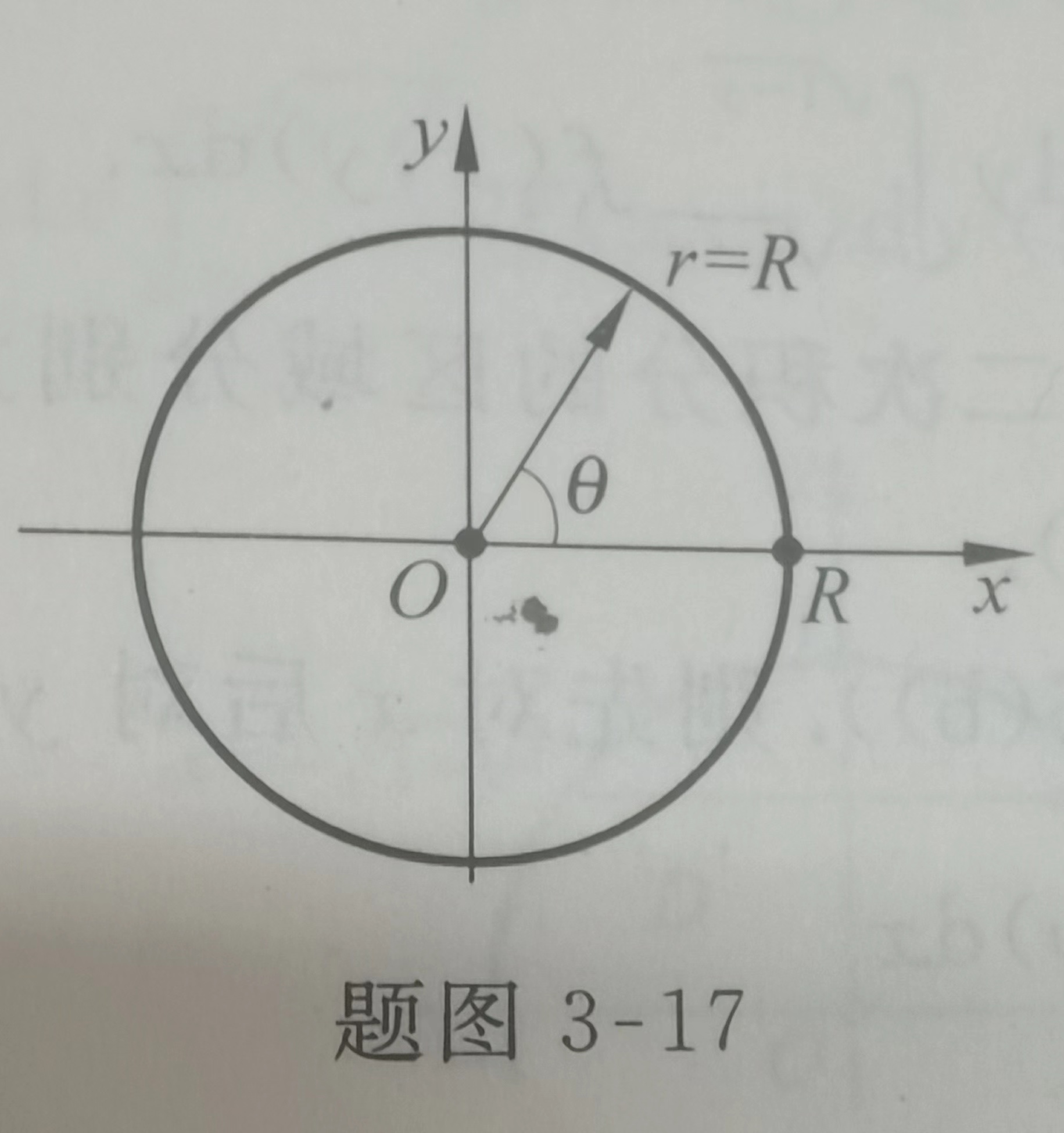
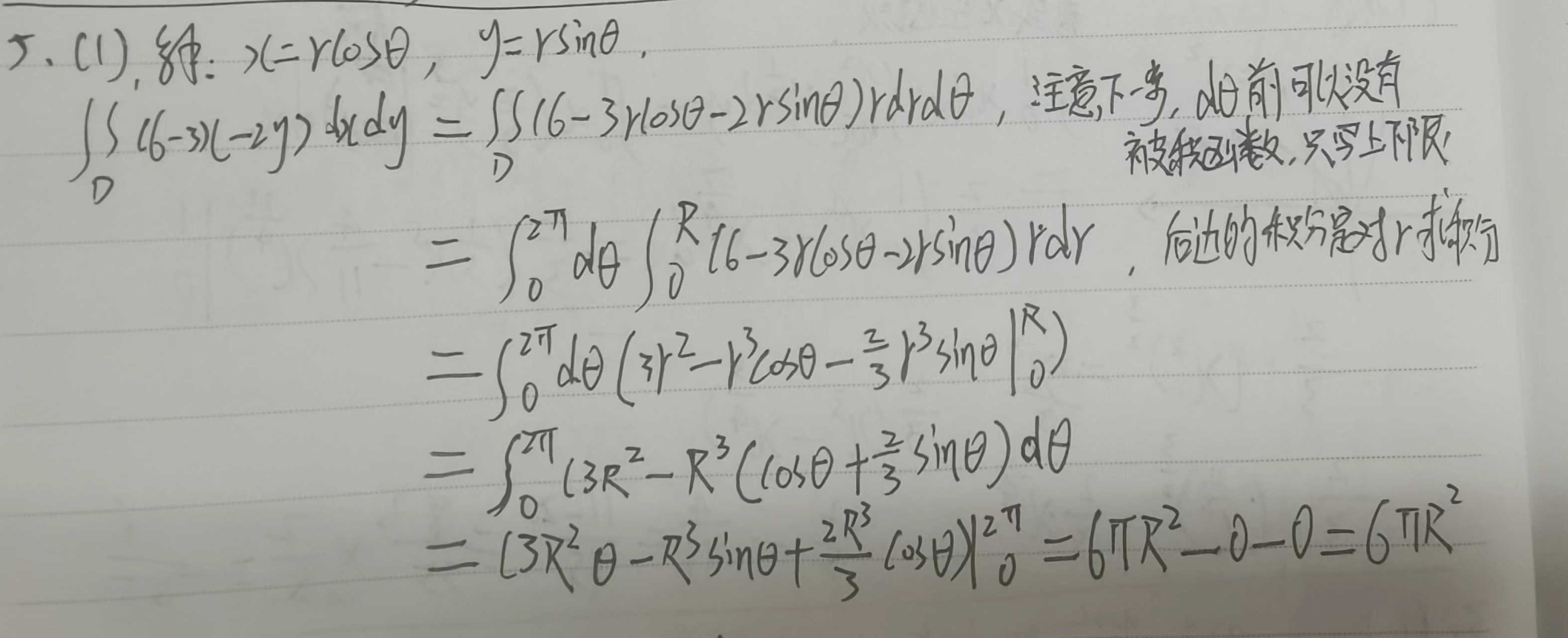
二.  如果积分区域D 由圆 或者 f(x, y)有  x² + y ² , 可以用极坐标来计算重积分