OpenGL学习07-OpenGL矩阵

最新推荐文章于 2023-06-05 17:48:18 发布

传涛

最新推荐文章于 2023-06-05 17:48:18 发布

阅读量524

点赞数

分类专栏： OpenGL学习文章标签： OpenGL 矩阵

本文链接：https://blog.csdn.net/xinchuantao/article/details/41897443

版权

OpenGL学习专栏收录该内容

10 篇文章 0 订阅

订阅专栏

关于矩阵的概念和矩阵的计算本篇就不再多说了，不了解的同学可以翻一下大学数学了！

矩阵(Matrix)是一种很强大的数学工具，特别实在计算机图形处理中，它可以极大的简化变量之间的复杂关系的一个或多个方程式的求解。例如：空间中有一个点坐标x、y、z，如果当这个点围绕任意点以任意方向旋转一定的坐标之后，想知道它的新位置，就需要使用矩阵。

（1）变换管线

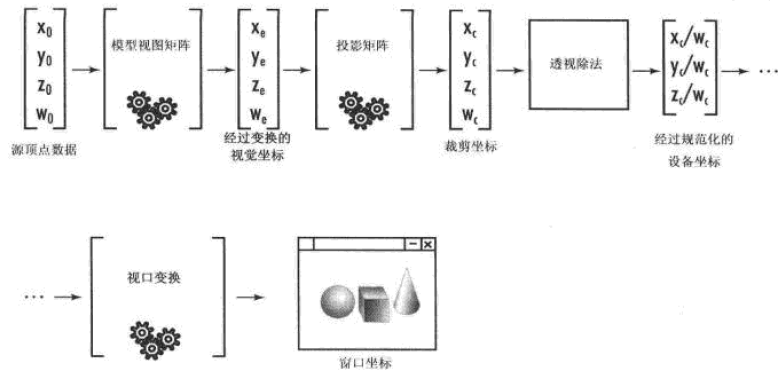
从原始顶点数据通往屏幕坐标的路是相当漫长的。图1提供了这个过程的流程图。

图1，来至OpenGL超级宝典

首先，把顶点转换成一个1 x 4的矩阵，前3个值分别是x、y、z，第4个是缩放因子，可以在接受4个参数的定制函数中手工使用这个值，这个值是w坐标，他在默认情况下为1.0，很少炫耀修改它。

接着，把顶点与模型视图矩阵相乘，产生经过变换的视觉坐标。

然后，将这个视觉坐标与投影矩阵相乘，产生裁剪坐标。这样就有效的清除了可视区域之外的所有数据。这个裁剪坐标随后除以w值，产生规范化的设备坐标。W值可能会被投影矩阵或者模型视图矩阵所修改，具体取决与顶点所发生的变换（OpenGL和高层矩阵函数隐藏了这些细节）。

最后，把这个坐标通过视口变换映射到一个2D平面上。

（2）模型视图矩阵

模型视图矩阵是一个4 x 4的矩阵，代表经过变换的坐标系统，我们可以用这个坐标系统放置物体并设置方向。为图元所提供的顶点按照单列单矩阵的形式使用，并与模型视图矩阵相乘，产生与视觉坐标相对应的经过变换的新坐标。

a)移动

使用Glut的函数库创建一个立方体，代码如下：

void glutWireCube(GLdouble size);

此时一个边长size个单位的立方体就会出现在原点居中的位置。如果希望在绘制这个立方体之前把它沿着y轴方向移动n个单位，可以把模型视图矩阵乘以一个表示沿y轴方向上移动n个单位的矩阵，然后执行绘制任务。

OpenGL提供了一个高层函数，可以实现这个操作，代码如下：

void glTranslatef (GLfloat x, GLfloat y, GLfloat z);

这个函数接受三个参数，分别是x、y、z方向的移动数量。然后，它创建一个适当的矩阵，并执行乘法操作。下面是上述操作的伪代码：

glTranslatef(0.0f, 50.0f, 0.0f);

glutWireCube(50.0f);

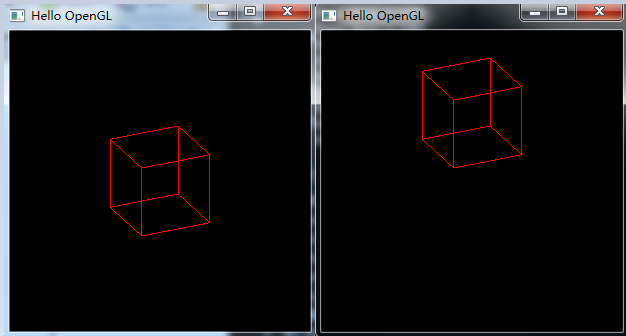
图2为移动前后的效果(图形旋转)：

图2

b）旋转

之前程序中一直在使用旋转功能，但我们仅仅只是会使用它，但还不知道旋转的原理。OpenGL高层提供了一个可以设置旋转矩阵的函数，如下：

void glRotatef (GLfloat angle, GLfloat x, GLfloat y, GLfloat z);

函数中接受4个参数，angle为旋转的角度，x、y、z为组成向量（x，y，z）为旋转围绕的轴。简单点来讲就是原点(0，0，0)和（x，y，z）组成一条直线，物理围绕这条直线旋转angle角度，下面是上述操作的伪代码：

glRotatef(45.0f, 1.0f, 1.0f, 1.0f);

glutWireCube(50.0f);

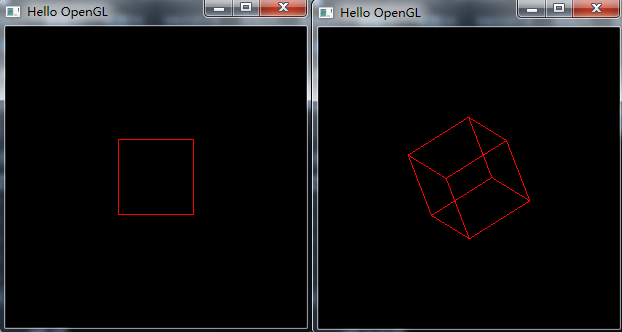
图3为旋转前后的效果：

图3

c)缩放

缩放变换根据指定的因子沿3个轴对物体的所有顶点惊醒拉伸或收缩，从而改变物体的大小。同样OpenGL高层提供了缩放的函数，如下：

void glScaled (GLdouble x, GLdouble y, GLdouble z);

函数接受3个参数，x、y、z分别为x、y、z方向的缩放比例因子，当缩放因子为1.0时，该方向大小不变；当缩放因子大于1.0时，该方向会被放大；当缩放因子小于1.0时，该方向会被缩小；下面是上述操作的伪代码：

glScaled(1.5f, 1.0f, 0.5f);

glutWireCube(50.0f);

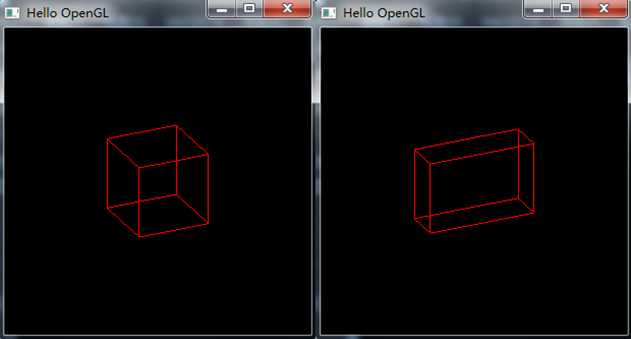
图4为缩放前后的效果(图形被旋转)：

图4

（3）单位矩阵

模型视图矩阵变换是累积的，每次调用一个变换函数时，都会创建一个新矩阵，并把它与当前的模型视图矩阵相乘，得到一个新矩阵作为当前模型视图矩阵。

可以通过在模型视图矩阵中加载单位矩阵来实现把模型视图矩阵重置到原点目标。单位矩阵表示没有反生变换，加载单位矩阵的效果相当于在绘图时所指定额所有坐标都处于视觉坐标中。所谓的单位矩阵就是矩阵对角线元素均为1，其余元素为0的矩阵。当这种矩阵与任意的顶点矩阵相乘时，其结果就是顶点矩阵，不会发生任何变化。如图5所示：

图5，来至OpenGL超级宝典

下面代码为加载单位矩阵：

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

第一行代码指定了当前操作的矩阵是模型视图矩阵。在设置了当前操作矩阵之后，他就将一直保持为活动矩阵，知道对他进行修改。第二行代码在当前矩阵中加载单位矩阵。

（4）矩阵堆栈

在场景中放置每个物体时，并不一定都要使用单位矩阵对模型视图矩阵重置。常常需要保存当前变换状态，然后放置了一些物体之后再进行恢复到这个状态。当一开始就报模式视图变换为自己经常使用的视图变换矩阵时，这种方法非常方便。

为了方便这个过程，OpenGL中维护了一个矩阵堆栈，它既可以用于模型视图矩阵，也可以用于投影矩阵，矩阵堆栈的工作方式就像普通堆栈一样。我们可以把当前的矩阵压入矩阵堆栈中，对它进行保存，然后再修改当前矩阵。从矩阵堆栈中弹出相当于恢复原来的那个矩阵。

堆栈的深度最大值获取：

glGetIntegerv(GL_MAX_MODELVIEW_STACK_DEPTH, &stack_deep);

矩阵堆栈操作函数：

glPushMatrix();

glPopMatrix();

glPushMatrix函数会将当前使用的模型视图矩阵压入堆栈；glPopMatrix函数会将栈顶的矩阵弹出，作为当前模型视图矩阵使用。

（5）矩阵高级操作

这些对变换(移动、缩放、旋转)进行包装的OpenGL高层函数对于许多变换问题是极为简单的。但是，为了获得真正强大的功能和灵活性，必须花时间掌握直接使用矩阵。

OpenGL在表示一个4x4的矩阵是并没有使用浮点型的二维数组，而是使用了一个包含16个浮点值的一维数组表示。这个方法和许多数学函数库使用的方法不同，后者常常使用二维数组来表示矩阵。例如,下面两个例子中，OpenGL更倾向于使用前者。

GLfloat matrix[16];

GLfloat matrix[4][4];

OpenGL也可以使用第二种类型表示形式，但是第一种是更高效的表示方式。这16个元素代表一个4x4的矩阵，如图6所示。当我们按列逐个遍历数组的元素是，就称之为列主序的矩阵顺序。在内存中，用二维数组表示4x4矩阵是以行主序存储的。

图6，来至OpenGL超级宝典

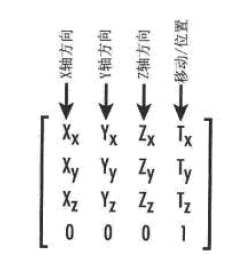
真正的奥秘在于这16个值表示空间中一个特定的位置和三个轴的方向。这4个列的每个列都表示一个4元素的向量。为了简单期间，我们把注意力集中在前3个元素中。第4列的那个向量包含了经过变换的坐标系统的x、y、x值。当我们在单位矩阵上调用glTranslate函数时，他所完成的任务就是把我们提供的x、y、z值放在这个矩阵的底12、13、14位置上。

前3列只是方向向量，便是空间中x、y、z轴的方向。在绝大多数情况下，这3个向量相互之间呈90度垂直(正交)，如图7所示；

最令人吃惊的事情是如果一个4x4的矩阵包含一个不同的坐标系统的位置和方向。那么，把一个顶点(以一个列矩阵或向量的形式)与这个矩阵相乘，其结果就是一个变换到该坐标的新顶点。这意味着空间中任何位置以及自己所需要的任何方向都可以通过一个4x4的矩阵进行唯一的定义，并且，如果把一个物体的所有顶点与这个矩阵相乘，就可以把整个物体变换到空间指定的位置和方向。