阵链乘法问题:
给定一个n个矩阵的序列(矩阵链)<A1, A2, A3, .……, An>,矩阵Ai的规模为Pi-1 * Pi, 求完全括号话方案,使得计算成绩A1*A2*......*An所需标量乘法次数最少。
注意:求解矩阵链乘法问题并不是要真正进行矩阵相乘运算,只是确定代价最低的计算顺序,确定最优计算书序所花费的时间通常要比随后真正进行矩阵相乘所节省的时间要少。
两个矩阵A、B相容,即A的列数等于B的行数时, 才能相乘。n个矩阵相乘有很多种计算方案,例如<A1, A2, A3, A4>
完全括号化的矩阵相乘链有
(A1(A2(A3 A4))
(A1((A2* A3)A4))
((A1 * A2)(A3* A4))
((A1(A2*A3)A4))
(((A1*A2)A3)A4)
但是每种相乘办法进行的乘法次数都不一样,这个问题即是是进行的乘法次数最少,求出分割点,并且给出最优化乘法链,运用的是自底向上的动态规划方法求解的
下面的两个m、s二维矩阵多用了一些空间,跟课本上的i, j标号保持了同步,便于理解,免去处理数组下标的很多问题。。。嘿嘿,有点偷懒....
#include <iostream>
#include <vector>
#include <algorithm>
#include <limits.h>
using namespace std;
pair<vector<vector<int> >, vector<vector<int> >>
matrixChainOrder(vector<int> p)
{
int n = p.size();
//m[i][j]保存Ai...j的代价也是最优值
vector<vector<int> > m(n, vector<int> (n, 0));
//s[i][j]记录m[i][j]最优解对应的分割点k
vector<vector<int> > s(n, vector<int> (n, 0));
//len是所求的矩阵链的长度
for (int len = 2; len < n; len++)
{
//计算m[i][j], i循环1...5
for (int i = 1; i <= n-len; i++)
{
int j = i+len-1; //j是矩阵链的终点,(2, 6)
m[i][j] = INT_MAX;
//k:(i, j), 计算中间的代价
for (int k = i; k < j; k++)
{
//m[i][j]的代价为m[i][k]与m[k+1][j]
//加上m[i][k]与m[k+1][j]的积(Ai,k与Ak+1,j的积为p[i-1]p[k]p[j])
int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (q < m[i][j])
{
m[i][j] = q;
s[i][j] = k;
}
}
}
}
cout << "vector m:" << endl;
for (int i = 0; i < n; i++)
{
copy(m[i].begin(), m[i].end(), ostream_iterator<int>(cout, " "));
cout << endl;
}
cout << "vector s:" << endl;
for (int i = 0; i < n; i++)
{
copy(s[i].begin(), s[i].end(), ostream_iterator<int>(cout, " "));
cout << endl;
}
return make_pair(m, s);
}
//打印→_→(最优括号化方案)
void printOptimalParens(vector<vector<int> > s, int i, int j)
{
if (i == j)
cout << "A" << i;
else
{
cout << "(";
printOptimalParens(s, i, s[i][j]);
printOptimalParens(s, s[i][j]+1, j);
cout << ")";
}
}
const int n = 7;
//一般递归方法
int recursiveMatrixChain(int (*m)[n], int *p, int i, int j)
{
if (i == j)
return 0;
m[i][j] = INT_MAX;
for (int k = i; k < j; k++)
{
int q = recursiveMatrixChain(m, p, i, k) +
recursiveMatrixChain(m, p, k+1, j) + p[i-1]*p[k]*p[j];
if (q < m[i][j])
m[i][j] = q;
}
return m[i][j];
}
//带备忘的自顶向下的递归方法实现
int lookUpChain(int (*m)[n], int *p, int i, int j)
{
if (m[i][j] != INT_MAX)
return m[i][j];
if (i == j)
m[i][j] = 0;
for (int k = i; k < j; k++)
{
int q = lookUpChain(m, p, i, k) +
lookUpChain(m, p, k+1, j) + p[i-1]*p[k]*p[j];
if (q < m[i][j])
m[i][j] = q;
}
return m[i][j];
}
//打印二维数组的右上半部分
void displayTwoArray(int (*twoArray)[n])
{
for (int i = 1; i < 7; i++)
{
for (int j = 1; j < 7; j++)
{
if (j <= i)
cout << " ";
else
cout << twoArray[i][j] << " ";
}
cout << endl;
}
}
int main()
{
int p[] = {30, 35, 15, 5, 10, 20, 25};
vector<int> ivp(p, p+sizeof(p)/sizeof(int));
cout << "自底向下的动态规划方法求解: " << endl;
printOptimalParens(matrixChainOrder(ivp).second, 1, 6);
cout << endl;
cout << "普通递归方法求解:";
int m[n][n];
cout << recursiveMatrixChain(m, p, 1, 6) << endl;
cout << "带备忘的递归方法求解:";
cout << lookUpChain(m, p, 1, 6) << endl;
system("pause");
return 0;
}运行结果为:(我把求出的两个二维数组也打印出来了...)








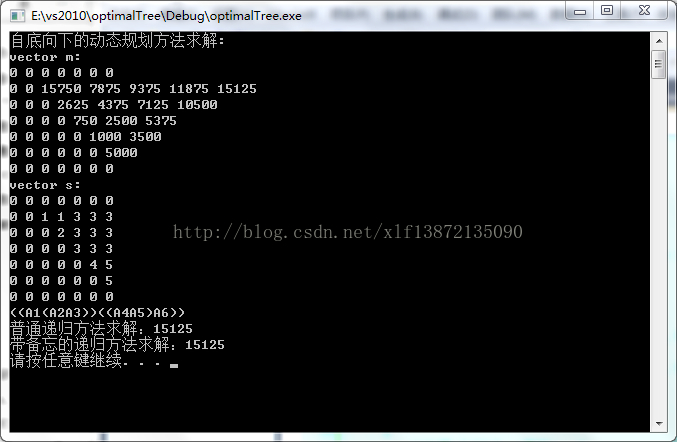














 278
278











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








