一张图搞定多变量微积分

Overview

此篇文章包含多变量微积分一些重点概念和一些重要应用。通过一些已有的结论和公式来解决现实中的问题。通过多变量微积分的学习让我对机器学习的一些算法了解的更加透彻。我并没有阐述公式的原理和其推导过程，但是，我会在相应主题的下面给你一些解释其原理的链接，如果想了解的话可以看看。

核心内容

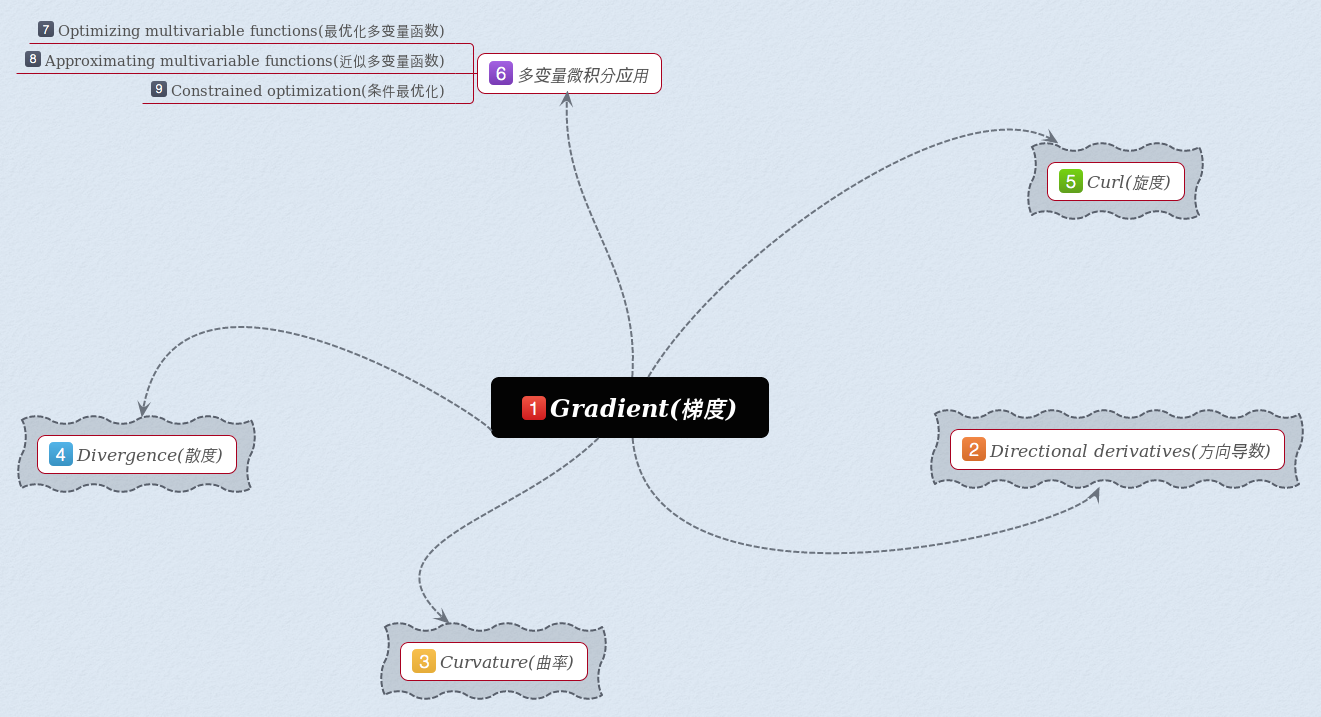
我自己画了一张思维导图，我会按照图上的标号依次阐述其具体内容。图片如下：

(一) 梯度

函数f的梯度表示为$\nabla f$，它是f所有偏微分的集合组成一个向量。例如：$f(x, y) = x^2 - xy$，它的梯度是$\nabla f(x, y) =\begin{bmatrix} \frac{\partial}{\partial x}(x^2 - xy)\\\frac{\partial}{\partial y}(x^2 - xy)\\ \end{bmatrix} = \begin{bmatrix} 2x - y\\ -x\end{bmatrix}$

对于函数f，在输入点$(x_0, y_0)$求得的梯度其方向为最快上升的方向（steepest ascent）。其具体原理：https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/gradient-and-directional-derivatives/a/the-gradient

(二) 方向导数

方向导数告诉你多变量函数$f$随着在给定向量$\vec{v}$的方向的输入下的变化率。

在给定$\vec{v}$的前提下，我们可以用$\nabla f * \vec{v}$来计算方向导数。

当方向导数用来计算斜率时，要将$\vec{v}$单位化。

其实我们可以认为$\nabla f * \vec{v}$是求导的通式。比如$f$为三维输入空间和一个输出：我们想求x方向的偏导，那么$\nabla f * \vec{v} = \begin{bmatrix} \frac{\partial f}{\partial x}\\\frac{\partial f}{\partial y}\\\frac{\partial f}{\partial z} \end{bmatrix} * \begin{bmatrix}1\\0\\0 \end{bmatrix} = \frac{\partial f}{\partial x}$

如果我把单位$\vec{v}$换成$\vec{v} * 2$，则上面导数的结果为 2∂f∂x<