本文详细介绍了图像处理中常见的四种插值算法：最近邻插值、线性插值、双线性插值和双三次插值。每种算法都有详细的解释和计算公式，帮助读者理解不同插值方法的特点及应用场景。
常见插值算法
在现实生活中，我们经常会遇到把图像进行放大、几何空间变换的情况等等，这些操作都需要在源图像和目标图像之间建立一个映射规则 ( x ′ , y ′ ) = T ( x , y ) \left(x^{\prime}, y^{\prime}\right)=T(x, y) (x′,y′)=T(x,y)，使得两图像像素坐标之间建立起一种对应关系，从而为目标图像的每一个像素赋值。
从源图像到目标图像的映射叫前向映射，但是这种映射方法可能会出现这样的两个问题：源图像的好几个像素点映射到目标图像中的位置是相同的；目标图像某些位置没有要赋值的像素。这样就要考虑如何把多个输出值转换成一个输出值和对目标图像中没有映射到的像素该如何赋值的问题。而我们经常采用的是后向映射，这种方法比前向映射更加有效，它是从目标图像到源图像的映射，即 ( x , y ) = T − 1 ( x ′ , y ′ ) (x, y)=T^{-1}\left(x^{\prime}, y^{\prime}\right) (x,y)=T−1(x′,y′),这样就避免了前向映射中存在的问题，但也不可避免地存在着部分像素映射回源图像时坐标为浮点数的问题，而图像的像素值仅在整数坐标处有定义，这时候就要利用图像插值方法来给这个待求像素点赋值。
常用的插值算法有：最近邻插值，双线性插值，双三次插值方法等等。其中最近邻插值方法（零阶插值）最简单，运算量最小，但是效果很差，块效应非常明显。
一、最邻插值算法
是最简单的一种插值算法，当图片放大时，缺少的像素通过直接使用与之最近原有颜色生成，也就是说照搬旁边的像素。这样做结果产生了明显可见的锯齿。
在待求象素的四邻象素中，将距离待求象素最近的邻灰度赋给待求象素。
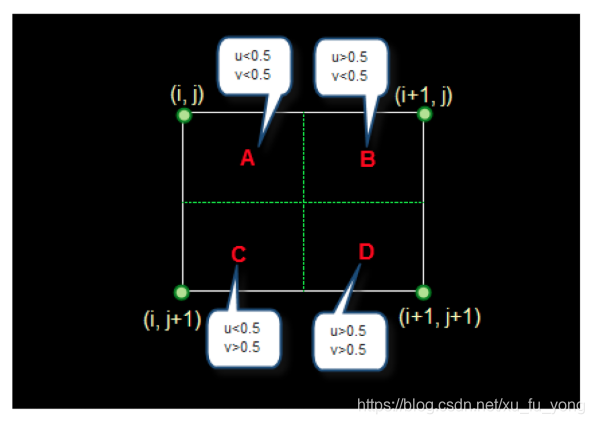
如果 i+u, j+v(i落在 A区，即 u<0.5,v<0.5，则将左上角象素的灰度值赋给待求象素，同理落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。
最近邻插值法计算量较小，但可能会造成生的图像灰度上的不连续，在变化地方可能出现明显锯齿状
二、线性插值
线性插值是一种针对一维数据的插值方法，它根据一维数据序列中需要插值的点的左右邻近两个数据点来进行数值的估计。当然了它不是求这两个点数据大小的平均值（当然也有求平均值的情况），而是根据到这两个点的距离来分配它们的比重的。
它很好地显示了线性插值的原理。根据图中的假设：已知点(x0,y0)、(x1,y1)，试问在x处插值，y的值是多少？用我们初中学过的知识，已知两个点的坐标可以得到一条线，又已知线上一点的一个坐标可以求得这个点的另一个坐标值。这就是线性插值的原理。
y
=
y
0
+
y
1
−
y
0
x
1
−
x
0
(
x
−
x
0
)
y=y 0+\frac{y 1-y 0}{x 1-x 0}(x-x 0)
y=y0+x1−x0y1−y0(x−x0)
这样就求得了y值。
三、双线性插值
双线性插值
假设源图像大小为mxn，目标图像为axb。那么两幅图像的边长比分别为：m/a和n/b。注意，通常这个比例不是整数，编程存储的时候要用浮点型。目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（im/a,jn/b）。显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。
若图像为灰度图像，那么（i，j）点的灰度值的数学计算模型是：
f(x,y)=b1+b2x+b3y+b4xy
其中b1,b2,b3,b4是相关的系数。关于其的计算过程如下如下：
如图，已知Q12，Q22，Q11，Q21，但是要插值的点为P点，这就要用双线性插值了，首先在x轴方向上，对R1和R2两个点进行插值，这个很简单，然后根据R1和R2对P点进行插值，这就是所谓的双线性插值。
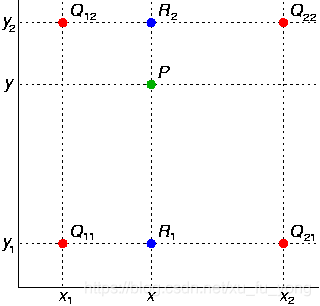
定义：双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
假如我们想得到未知函数
f
f
f在点
P
=
(
x
,
y
)
P=(x, y)
P=(x,y)的值，假设我们已知函数
f
f
f 在
Q
11
=
(
x
1
,
y
1
)
,
Q
12
=
(
x
1
,
y
2
)
,
Q
21
=
(
x
2
,
y
1
)
Q_{11}=\left(x_{1}, y_{1}\right), Q_{12}=\left(x_{1}, y_{2}\right), Q_{21}=\left(x_{2}, y_{1}\right)
Q11=(x1,y1),Q12=(x1,y2),Q21=(x2,y1)及
Q
22
=
(
x
2
,
y
2
)
Q_{22}=\left(x_{2}, y_{2}\right)
Q22=(x2,y2) 四个点的值。
首先在 x 方向进行线性插值，得到
f
(
R
1
)
≈
x
2
−
x
x
2
−
x
1
f
(
Q
11
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
21
)
Where
R
1
=
(
x
,
y
1
)
f
(
R
2
)
≈
x
2
−
x
x
2
−
x
1
f
(
Q
12
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
22
)
Where
R
2
=
(
x
,
y
2
)
\begin{aligned} f\left(R_{1}\right) & \approx \frac{x_{2}-x}{x_{2}-x_{1}} f\left(Q_{11}\right)+\frac{x-x_{1}}{x_{2}-x_{1}} f\left(Q_{21}\right) \quad \text { Where } \quad R_{1}=\left(x, y_{1}\right) \\ f\left(R_{2}\right) & \approx \frac{x_{2}-x}{x_{2}-x_{1}} f\left(Q_{12}\right)+\frac{x-x_{1}}{x_{2}-x_{1}} f\left(Q_{22}\right) \quad \text { Where } \quad R_{2}=\left(x, y_{2}\right) \end{aligned}
f(R1)f(R2)≈x2−x1x2−xf(Q11)+x2−x1x−x1f(Q21) Where R1=(x,y1)≈x2−x1x2−xf(Q12)+x2−x1x−x1f(Q22) Where R2=(x,y2)
然后在 y 方向进行线性插值，得到
f
(
P
)
≈
y
2
−
y
y
2
−
y
1
f
(
R
1
)
+
y
−
y
1
y
2
−
y
1
f
(
R
2
)
f(P) \approx \frac{y_{2}-y}{y_{2}-y_{1}} f\left(R_{1}\right)+\frac{y-y_{1}}{y_{2}-y_{1}} f\left(R_{2}\right)
f(P)≈y2−y1y2−yf(R1)+y2−y1y−y1f(R2)
这样就得到所要的结果
f
(
x
,
y
)
f(x, y)
f(x,y),
f
(
x
,
y
)
≈
f
(
Q
11
)
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
2
−
x
)
(
y
2
−
y
)
+
f
(
Q
21
)
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
−
x
1
)
(
y
2
−
y
)
+
f
(
Q
12
)
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
2
−
x
)
(
y
−
y
1
)
+
f
(
Q
22
)
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
−
x
1
)
(
y
−
y
1
)
\begin{array}{c}{f(x, y) \approx \frac{f\left(Q_{11}\right)}{\left(x_{2}-x_{1}\right)\left(y_{2}-y_{1}\right)}\left(x_{2}-x\right)\left(y_{2}-y\right)+\frac{f\left(Q_{21}\right)}{\left(x_{2}-x_{1}\right)\left(y_{2}-y_{1}\right)}\left(x-x_{1}\right)\left(y_{2}-y\right)} \\ {+\frac{f\left(Q_{12}\right)}{\left(x_{2}-x_{1}\right)\left(y_{2}-y_{1}\right)}\left(x_{2}-x\right)\left(y-y_{1}\right)+\frac{f\left(Q_{22}\right)}{\left(x_{2}-x_{1}\right)\left(y_{2}-y_{1}\right)}\left(x-x_{1}\right)\left(y-y_{1}\right)}\end{array}
f(x,y)≈(x2−x1)(y2−y1)f(Q11)(x2−x)(y2−y)+(x2−x1)(y2−y1)f(Q21)(x−x1)(y2−y)+(x2−x1)(y2−y1)f(Q12)(x2−x)(y−y1)+(x2−x1)(y2−y1)f(Q22)(x−x1)(y−y1)
如果选择一个坐标系统使得
f
f
f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为
f
(
x
,
y
)
≈
f
(
0
,
0
)
(
1
−
x
)
(
1
−
y
)
+
f
(
1
,
0
)
x
(
1
−
y
)
+
f
(
0
,
1
)
(
1
−
x
)
y
+
f
(
1
,
1
)
x
y
f(x, y) \approx f(0,0)(1-x)(1-y)+f(1,0) x(1-y)+f(0,1)(1-x) y+f(1,1) x y
f(x,y)≈f(0,0)(1−x)(1−y)+f(1,0)x(1−y)+f(0,1)(1−x)y+f(1,1)xy
或者用矩阵运算表示为:
f
(
x
,
y
)
≈
[
1
−
x
x
]
[
f
(
0
,
0
)
f
(
0
,
1
)
f
(
1
,
0
)
f
(
1
,
1
)
]
[
1
−
y
y
]
f(x, y) \approx\left[\begin{array}{cc}{1-x} & {x}\end{array}\right]\left[\begin{array}{cc}{f(0,0)} & {f(0,1)} \\ {f(1,0)} & {f(1,1)}\end{array}\right]\left[\begin{array}{c}{1-y} \\ {y}\end{array}\right]
f(x,y)≈[1−xx][f(0,0)f(1,0)f(0,1)f(1,1)][1−yy]
线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。
注意： 源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下：
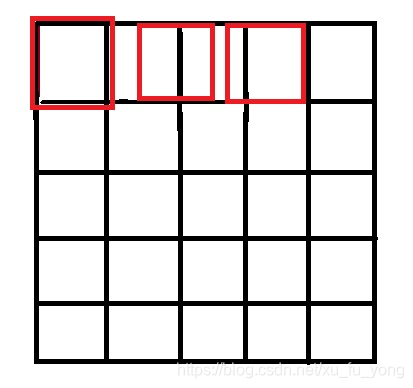
只画了一行，用做示意，从图中可以很明显的看到，如果选择右上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。
那么，让坐标加1或者选择右下角为原点怎么样呢？很不幸，还是一样的效果，不过这次得到的图像将偏右偏下。
最好的方法就是，两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距，这也是matlab和openCV的做法。如下图：
计算对应坐标的时候改为以下公式即可：
int
x
=
(
i
+
0.5
)
∗
m
/
a
−
0.5
int
y
=
(
j
+
0.5
)
∗
n
/
b
−
0.5
\begin{array}{l}{\text { int } x=(i+0.5)^{*} \mathrm{m} / \mathrm{a}-0.5} \\ {\text { int } y=(j+0.5)^{*} \mathrm{n} / \mathrm{b}-0.5}\end{array}
int x=(i+0.5)∗m/a−0.5 int y=(j+0.5)∗n/b−0.5
代替
int
x
=
i
⋆
m
/
a
int
y
=
j
⋆
n
/
b
\begin{array}{l}{\text { int } \mathrm{x}=\mathrm{i}^{\star} \mathrm{m} / \mathrm{a}} \\ {\text { int } \mathrm{y}=\mathrm{j}^{\star} \mathrm{n} / \mathrm{b}}\end{array}
int x=i⋆m/a int y=j⋆n/b
四、双三次(bicubic)插值
双三次插值又称立方卷积插值。三次卷积插值是一种更加复杂的插值方式。该算法利用待采样点周围16个点的灰度值作三次插值，不仅考虑到4 个直接相邻点的灰度影响，而且考虑到各邻点间灰度值变化率的影响。三次运算可以得到更接近高分辨率图像的放大效果，但也导致了运算量的急剧增加。这种算法需要选取插值基函数来拟合数据，其最常用的插值基函数如下所示：
构造BiCubic函数：
W
(
x
)
=
{
(
a
+
2
)
∣
x
∣
3
−
(
a
+
3
)
∣
x
∣
2
+
1
for
∣
x
∣
≤
1
a
∣
x
∣
3
−
5
a
∣
x
∣
2
+
8
a
∣
x
∣
−
4
a
for
1
<
∣
x
∣
<
2
0
otherwise
W(x)=\left\{\begin{array}{ll}{(a+2)|x|^{3}-(a+3)|x|^{2}+1} & {\text { for }|x| \leq 1} \\ {a|x|^{3}-5 a|x|^{2}+8 a|x|-4 a} & {\text { for } 1<|x|<2} \\ {0} & {\text { otherwise }}\end{array}\right.
W(x)=⎩⎨⎧(a+2)∣x∣3−(a+3)∣x∣2+1a∣x∣3−5a∣x∣2+8a∣x∣−4a0 for ∣x∣≤1 for 1<∣x∣<2 otherwise
其中，a取-0.5.
BiCubic函数具有如下形状：
假设源图像A大小为mn，缩放后的目标图像B的大小为MN。那么根据比例我们可以得到B(X,Y)在A上的的 对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))。在双线性插值法中，我们选取A(x,y)的最近四个点。而在双立方 插值法中，我们选取的是最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数。如图所示：
每个像素值的权重由该点到待求像素点的距离确定，这个距离包括水平和竖直两个方向上的距离。以像素点为例，该点在竖直和水平方向上与待求像素点的距离分别是
1
+
u
1+u
1+u和
v
v
v则该像素点的权重为
w
=
w
(
1
+
u
)
×
w
(
v
)
w=w(1+u) \times w(v)
w=w(1+u)×w(v)。则待求点像素值
f
(
i
+
u
,
j
+
v
)
f(i+u, j+v)
f(i+u,j+v)的计算方法如下式所示。
f
(
i
+
u
,
j
+
v
)
=
A
×
B
×
C
f(i+u, j+v)=A \times B \times C
f(i+u,j+v)=A×B×C
其中：
A
=
[
w
(
1
+
u
)
w(u)
w
(
1
−
u
)
w
(
2
−
u
)
]
\mathrm{A}=[w(1+u) \text { w(u) } w(1-u) w(2-u)]
A=[w(1+u) w(u) w(1−u)w(2−u)]
C
=
[
w
(
1
+
v
)
w
(
v
)
w
(
1
−
v
)
w
(
2
−
v
)
]
T
\mathrm{C}=[w(1+v) \quad w(v) \quad w(1-v) \quad w(2-v)]^{T}
C=[w(1+v)w(v)w(1−v)w(2−v)]T
B
=
[
f
(
i
−
1
,
j
−
1
)
f
(
i
−
1
,
j
+
0
)
f
(
i
−
1
,
j
+
1
)
f
(
i
−
1
,
j
+
2
)
f
(
i
+
0
,
j
−
1
)
f
(
i
+
0
,
j
+
0
)
f
(
i
+
0
,
j
+
1
)
f
(
i
+
0
,
j
+
2
)
f
(
i
+
1
,
j
−
1
)
f
(
i
+
1
,
j
+
0
)
f
(
i
+
1
,
j
+
1
)
f
(
i
+
1
,
j
+
2
)
f
(
i
+
2
,
j
−
1
)
f
(
i
+
2
,
j
+
0
)
f
(
i
+
2
,
j
+
1
)
f
(
i
+
2
,
j
+
2
)
]
B=\left[\begin{array}{llllll}{f(i-1, j-1)} & {f(i-1, j+0)} & {f(i-1, j+1)} & {f(i-1, j+2)} \\ {f(i+0, j-1)} & {f(i+0, j+0)} & {f(i+0, j+1)} & {f(i+0, j+2)} \\ {f(i+1, j-1)} & {f(i+1, j+0)} & {f(i+1, j+1)} & {f(i+1, j+2)} \\ {f(i+2, j-1)} & {f(i+2, j+0)} & {f(i+2, j+1)} & {f(i+2, j+2)}\end{array}\right]
B=⎣⎢⎢⎡f(i−1,j−1)f(i+0,j−1)f(i+1,j−1)f(i+2,j−1)f(i−1,j+0)f(i+0,j+0)f(i+1,j+0)f(i+2,j+0)f(i−1,j+1)f(i+0,j+1)f(i+1,j+1)f(i+2,j+1)f(i−1,j+2)f(i+0,j+2)f(i+1,j+2)f(i+2,j+2)⎦⎥⎥⎤
插值核
w
(
x
)
w(x)
w(x)为:
w
(
x
)
=
{
1
−
2
∣
x
∣
2
+
∣
x
∣
3
,
∣
x
∣
<
1
4
−
8
∣
x
∣
+
5
∣
x
∣
2
−
∣
x
∣
3
,
1
≤
∣
x
∣
<
2
0
,
∣
x
∣
≥
2
w(x)=\left\{\begin{array}{cc}{1-2|x|^{2}+|x|^{3}} & {,|x|<1} \\ {4-8|x|+5|x|^{2}-|x|^{3},} & {1 \leq|x|<2} \\ {0} & {, \quad|x| \geq 2}\end{array}\right.
w(x)=⎩⎨⎧1−2∣x∣2+∣x∣34−8∣x∣+5∣x∣2−∣x∣3,0,∣x∣<11≤∣x∣<2,∣x∣≥2
扫一扫
502
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
