旋转矩阵
两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去
在三维世界的坐标变换中,我们经常用一个旋转矩阵来旋转一个点,比如:
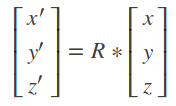

绕任意轴旋转则可以分解成绕三个坐标轴旋转的叠加,最终得到的旋转矩阵 R 便是上述三个矩阵的乘积。
然而,用矩阵来表示一个旋转关系有两个缺点:
首先,通过旋转矩阵不能直观地看出旋转的方向和角度,假设给定一个旋转矩阵,要求旋转方向不变,旋转角度变成一半,那么新的旋转矩阵计算起来就比较麻烦了。
另一方面,旋转变换本身只有3个自由度,但旋转矩阵有9个元素,因此旋转矩阵中的元素不是相互独立的,这在非线性优化中会带来问题。
旋转向量
向量旋转公式最早由 Rodrigues 提出,用一个三维向量来表示三维旋转变换,该向量的方向是旋转轴,其模则是旋转角度。百度百科中有其详细的介绍与推导,我在这边只列一下最重要的公式。
设旋转向量的单位向量为 r,模为 θ。三维点(或者说三维向量)p 在旋转向量 r 的作用下变换至 p′,则:

这个公式和罗德里格斯公式很像。
相互转换
设旋转向量的单位向量 r=[rx ry rz]T,旋转角度为 θ,对应的旋转矩阵为 R,则 r 到 R 的转换是:

其中 I 是三阶单位矩阵。反过来 R 到 r 的转换则可以利用等式:
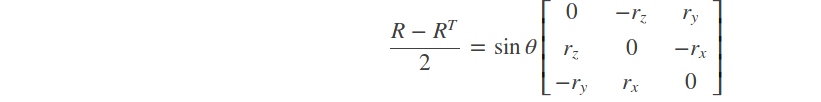

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










